11 класс геометрия карточки цилиндр

Видео:ГЕОМЕТРИЯ 11 класс: Цилиндр. Площадь поверхностиСкачать

Задачи для самопроверки по теме: «Цилиндр, конус, сфера»
тренажёр по геометрии (11 класс) на тему

данный материал поможет учителям при проверке усвоенного материала

Видео:Видеоурок по математике "Цилиндр"Скачать

Скачать:

Как сдать ЕГЭ на 80+ баллов?

Репетиторы Учи.Дома помогут подготовиться к ЕГЭ. Приходите на бесплатный пробный урок, на котором репетиторы определят ваш уровень подготовки и составят индивидуальный план обучения.

Бесплатно, онлайн, 40 минут

Видео:Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

Предварительный просмотр:

Задачи для самопроверки по теме: «Цилиндр, конус, сфера»

1. Высота конуса равна 15, а диаметр основания – 16. Найти образующую конуса.
2. Площадь боковой поверхности конуса равна 16 см 2 . Радиус основания конуса уменьшили в 4 раза, а образующую увеличили в 2 раза. Найти площадь боковой поверхности получившегося конуса.
3. Площадь боковой поверхности конуса равна 10 см 2 . Радиус основания конуса увеличили в 6 раз, а образующую уменьшили в 4 раза. Найти площадь боковой поверхности получившегося конуса.
4. Площадь боковой поверхности цилиндра равна 16П, а высота – 2. Найти диаметр основания цилиндра.
5. Площадь боковой поверхности цилиндра равна 21П, а диаметр основания равен 7. Найти высоту цилиндра.
6. Радиус основания конуса равен 3, высота равна 4. Найти площадь поверхности конуса, деленную на П.
7. Площадь боковой поверхности цилиндра равна 40П, а высота – 4. Найти площадь поверхности цилиндра, деленную на П.
8. Площадь большого круга шара равна 3. Найти площадь поверхности шара.
9. Дано два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
10. Дано два шара с радиусами 8 и 4. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
11. Сечение шара площадью 64П находится на расстоянии 6 см от центра шара. Найти площадь поверхности шара, деленную на П.
12. Расстояние от центра шара радиуса 12 см до секущей плоскости равно 8 см. Найти площадь сечения, деленную на П.
13. Радиусы двух шаров равны 14 и 48. Найти радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
14. Около шара описан цилиндр, площадь поверхности которого равна 162. Найти площадь поверхности шара.
15. Около конуса описана сфера. Центр сферы совпадает с центром основания конуса. Найти радиус сферы, если образующая конуса равна 40√2.
16. Около конуса описана сфера. Центр сферы совпадает с центром основания конуса. Найти образующую конуса, если радиус сферы 5√2.

Видео:Объем цилиндра. Практическая часть. 11 класс.Скачать

По теме: методические разработки, презентации и конспекты

Открытый урок по геометрии 11 класс по теме: «Цилиндр. Конус.»

Урок обобщения и систематизации знаний. Подготовка к ЕГЭ.

Зачет по теме «Цилиндр. Конус. Шар»

Урок по геометрии – 11 класс (УМК Атанасян Л.С), с использованием ИТ в т.ч. Интернета.Цель урока: проверить теоретические и практические знания по данной теме.

Читайте также: Момент затяжки блока цилиндров приора

Контрольная работа по геометрии для 11 класса по теме «Цилиндр, конус, сфера и шар»

Контрольная работа по геометрии для 11 класса по теме «Цилиндр, конус, сфера и шар» в 2-х вариантах.

Урок — семинар по геометрии на тему » Цилиндр, конус, усеченный конус»

Разроботка урока — семинара по геометрии на тему » Цилиндр, конус, усеченный конус».

Урок по теме «Цилиндр. Конус. Усеченный конус», 11 класс

Разработка урока-игры по теме «Цилиндр. Конус. Усеченный конус.» в 11 классе по геометрии.

Урок геометрии в 11 классе по теме «Цилиндр. Конус. Усеченный конус»

Урок геометрии в 11 классе по теме «Цилиндр. Конус. Усеченный конус&quot.

Контрольная работа по теме: «Цилиндр, конус, шар и сфера»

Контроольная работа для 11 общеобразовательного класса.

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Карточки-задания по теме «Объем цилиндра»

Самостоятельная работа по теме: « Объем цилиндра»

Дано: цилиндр, Н =10 см, d = OK = 9 см (расстояние от центра основания до сечения)

АА 1 В 1 В – сечение, АА 1 В 1 В || ОО 1 , S сеч = 240 дм 2 .

Задача. Отрезок АВ 1 , концы которого лежат на разных окружностях оснований цилиндра, пересекает ось цилиндра под углом 45 о . Найдите объем цилиндра, если длина отрезка АВ 1 равна 4см.

Задача: Объем цилиндра равен 36 см 3 , а площадь осевого сечения 36см 2 . Найдите радиус основания цилиндра.

Цилиндр получен вращением прямоугольника АВС D вокруг прямой ВС. Найдите объем цилиндра, если АВ=3см, ВС=6см.

№ 667. Алюминиевый провод диаметром 4 мм имеет массу 6,8 кг. Найдите длину провода (плотность алюминия 2,6г/см 3 ).

№ 668. Какое количество нефти (в тоннах) вмещает цилиндрическая цистерна диаметром 18 м и высотой 7 м, если плотность нефти равна

№ 670. Свинцовая труба (плотность свинца 11,4 г/см 3 ) с толщиной стенок 4 мм имеет внутренний диаметр 13 мм. Какова масса трубы, если ее длина равна 25 м?

c 2 = a 2 + b 2 – теорема Пифагора (квадрат гипотенузы равен сумме квадратов катетов)

Видео:59. Понятие цилиндраСкачать

Задания для подготовки к ЕГЭ 11 класс «Цилиндр»»
материал для подготовки к егэ (гиа, 11 класс) на тему

Задания для подготовки к ЕГЭ 11 класс «Цилиндр»

Видео:Объём цилиндраСкачать

Скачать:

Как сдать ЕГЭ на 80+ баллов?

Репетиторы Учи.Дома помогут подготовиться к ЕГЭ. Приходите на бесплатный пробный урок, на котором репетиторы определят ваш уровень подготовки и составят индивидуальный план обучения.

Бесплатно, онлайн, 40 минут

Видео:11 класс, 14 урок, Понятие цилиндраСкачать

Предварительный просмотр:

МБОУ Пожарская СОШ Сергачского района Нижегородской области

Учитель математики первой категории Зюляева Л.Ю.

Задания для подготовки к ЕГЭ

Задачи по готовым чертежам

1. Осевое сечение цилиндра – квадрат со стороной 6 см. Найти сумму высоты и радиуса основания цилиндра.

2. Радиус основания цилиндра равен 2м, высота 3м. Найти диагональ осевого сечения.

3. Длина окружности основания цилиндра равна 1. Площадь боковой поверхности равна 2. Найдите высоту цилиндра.

Задачи по готовым чертежам

1. Осевое сечение цилиндра – квадрат со стороной 8 см. Найти сумму высоты и радиуса основания цилиндра.

Читайте также: После капремонта двигателя нет компрессии в одном цилиндре

2. Радиус основания цилиндра равен 4м, высота 6м. Найти диагональ осевого сечения.

3. Длина окружности основания цилиндра равна 2. Площадь боковой поверхности равна 1. Найдите высоту цилиндра.

Типы задач на ЕГЭ по теме «Площадь боковой поверхности цилиндра»

1 Диагональ осевого сечения цилиндра равна 48. Угол между этой диагональю и образующей равен 30 0 . Найдите радиус цилиндра.

2. Радиус основания цилиндра равен 6, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π.

3. Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 45 0 и равна 8√2 см. Найдите площадь боковой поверхности цилиндра, деленную на π .

4. Во сколько раз увеличится площадь боковой поверхности цилиндра, если его высоту и радиус увеличить в три раза?

Задачи, решаемые в одно действие с помощью т. Пифагора или свойства прямоугольного треугольника

Задачи, решаемые в одно действие с помощью формулы площади боковой поверхности.

Задачи, решаемые в два действия с помощью т. Пифагора и формулы площади боковой поверхности.

Задания по теме «Площадь поверхности цилиндра»

ЕГЭ 2015 Задания из Открытого банка заданий. Математика. Геометрия.

Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.

Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.

Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π .

Проверочная тестовая работа Вариант 1

№1. Радиус основания цилиндра равен 2 см, высота – 5 см, тогда площадь боковой поверхности, деленная на π, равна:

№2. В цилиндре радиуса осевым сечением является квадрат, а площадь основания равна 16 π кв.дм. Найдите площадь полной поверхности цилиндра деленную на π .

№3. Радиус основания цилиндра в два раза меньше образующей, равной 4, тогда площадь боковой поверхности, деленная на π, равна:

№4. Площадь полной поверхности цилиндра, полученного вращением прямоугольника со сторонами 4 см и 7 см вокруг его большей стороны, деленная на π, равна:

№5. Если площадь боковой поверхности цилиндра равна 64 π кв.м, а высота – 4 м, тогда радиус равен:

№6. Осевым сечением цилиндра является прямоугольник со сторонами 10 и 16 см, то площадь основания цилиндра, деленная на π, может быть равна:

№7. Осевым сечением цилиндра является прямоугольник со сторонами 12 и 8 см, то площадь боковой поверхности цилиндра, деленная на π, может быть равна:

Проверочная тестовая работа

№1. Диаметр основания цилиндра равен 4 см, высота – 3 см, тогда площадь боковой поверхности, деленная на π, равна:

№2. В цилиндре радиуса осевым сечением является квадрат, а площадь основания равна 9 π кв.дм. Найдите площадь полной поверхности цилиндра деленную на π .

№3. Радиус основания цилиндра в три раза меньше образующей, равной 6, тогда площадь боковой поверхности, деленная на π, равна:

№4 . Площадь полной поверхности цилиндра, полученного вращением прямоугольника со сторонами 4 см и 7 см вокруг его меньшей стороны, деленная на π , равна:

Читайте также: Опель вектра замена прокладки блока цилиндров

№5. Если площадь боковой поверхности цилиндра равна 64 π кв.м, а радиус – 8м, тогда образующая равна:

№6. Осевым сечением цилиндра является прямоугольник со сторонами 10 и 16 см, то площадь основания цилиндра, деленная на π, может быть равна:

№7. Осевым сечением цилиндра является прямоугольник со сторонами 6 и 8 см, то площадь боковой поверхности цилиндра может быть равна:

Видео:11 класс, 19 урок, Сфера и шарСкачать

Зачет по теме «Цилиндр, конус, шар»

Карточки для зачета по геометрии в 11 классе

Содержимое разработки

Зачет11_02 по теме:«Цилиндр, конус и шар».

Объясните, какое тело называется цилиндром. Выведите формулу площади полной поверхности цилиндра.

Высота конуса равна 6 см., а образующая наклонена к плоскости основания под углом в 30 о . Найдите площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 60 о .

Радиус шара равен R. Найдите площадь поверхности вписанного в шар куба.

Зачет11_02 по теме:«Цилиндр, конус и шар».

Объясните, какое тело называется конусом. Выведите формулу площади полной поверхности конуса.

Радиус шара равен 8 см. Через конец радиуса, лежащего на сфере, проведена плоскость под углом 45 о к радиусу. Найдите площадь сечения шара этой плоскостью.

Куб с ребром а вписан в цилиндр. Найдите площадь осевого сечения цилиндра.

Зачет11_02 по теме:«Цилиндр, конус и шар».

Объясните, какое тело называется усеченным конусом. Выведите формулу площади полной поверхности усеченного конуса.

Сечение цилиндра плоскостью, параллельной оси, отсекает от окружности основания дугу в 90 о . Найдите площадь сечения, если высота цилиндра равна 6 см., а расстояние между осью цилиндра и секущей плоскостью равна 3 см.

Около шара радиуса R описан правильный тетраэдр. Найдите площадь поверхности тетраэдра.

Зачет11_02 по теме:«Цилиндр, конус и шар».

Объясните, какая поверхность называется сферой и какое тело называется шаром. Выведите уравнение сферы в заданной прямоугольной системе координат.

Радиус кругового сектора равен 6 см., а его угол равен 120 о . Сектор свернут в коническую поверхность. Найдите площадь полной поверхности конуса.

Осевое сечение конуса – равносторонний треугольник. В конус вписана треугольная пирамида, основанием которой служит прямоугольный треугольник с катетами 12 см и 16 см. Найдите высоту пирамиды.

Зачет11_02 по теме:«Цилиндр, конус и шар».

Перечислите возможные случаи взаимного расположения сферы и плоскости. Докажите, что сечение сферы плоскостью есть окружность.

Осевое сечение цилиндра – квадрат, диагональ которого равна 12 см. Найдите площадь боковой поверхности цилиндра.

В сферу вписан конус, образующая которого равна l, а угол при вершине осевого сечения равен 60 о . Найдите площадь сферы.

Зачет11_02 по теме:«Цилиндр, конус и шар».

Сформулируйте определение касательной плоскости к сфере. Докажите теоремы о касательной плоскости (свойство и признак касательной плоскости).

Площадь сечения шара плоскостью, проходящей через его центр, равна 16 см 2 . Найдите площадь сферы.

Диагональ правильной четырехугольной призмы равна 4 см и наклонена к плоскости основания под углом 45 о . Найдите площадь боковой поверхности цилиндра, вписанного в эту призму.

🔥 Видео

Объем цилиндра. Урок 13. Геометрия 11 классСкачать

Призма и цилиндр. Практическая часть. 11 класс.Скачать

Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

11 класс, 15 урок, Площадь поверхности цилиндраСкачать

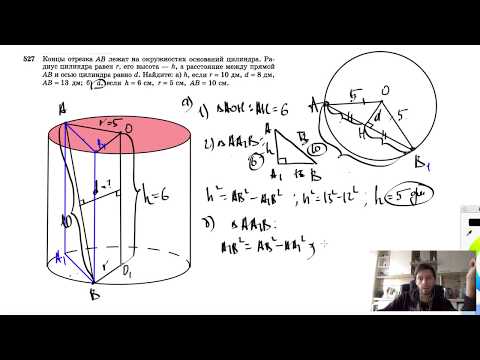
№527. Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус цилиндра равен г,Скачать

11 класс, 32 урок, Объем цилиндраСкачать

Геометрия 11 класс: Объем призмы и цилиндра. ВидеоурокСкачать

11 класс. Геометрия. Объем цилиндраСкачать

Геометрия. 11 класс. Цилиндр и его элементыСкачать