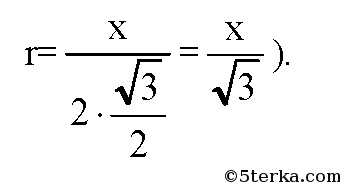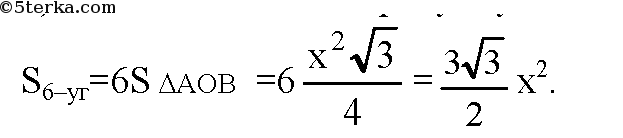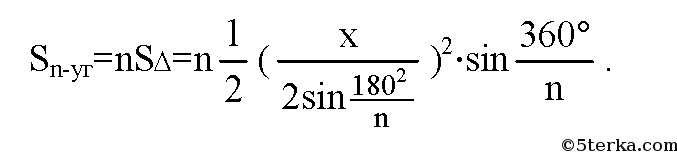671 в цилиндр вписана (7 видео)

Содержание

671. В цилиндр вписана правильная n-угольная призма. Найдите отношение объемов призмы и цилиндра, если: а) n = 3; б) n = 4; в) n=6; г) n = 8; д) n произвольное целое число.
671. В цилиндр вписана правильная n-угольная призма. Найдите отношение объемов призмы и цилиндра, если: а) n = 3; б) n = 4; в) n=6; г) n = 8; д) n произвольное целое число
671 в цилиндр вписана
671 в цилиндр вписана
Задача. Призма, вписанная в цилиндр
Задача. В цилиндр вписана правильная шестиугольная призма
Решение №2305 Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3.
📹 Видео

Видео:№ 671 - Геометрия 10-11 класс АтанасянСкачать

671. В цилиндр вписана правильная n-угольная призма. Найдите отношение объемов призмы и цилиндра, если: а) n = 3; б) n = 4; в) n=6; г) n = 8; д) n произвольное целое число.

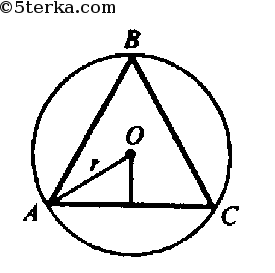
а) n=3, ΔАВС — правильный. Обозначим сторону ΔАВС равной х, следовательно,

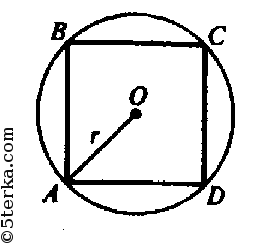
б) n=4, ABCD — квадрат. Обозначим сторону квадрата равной х.

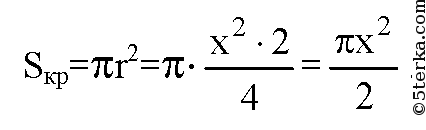
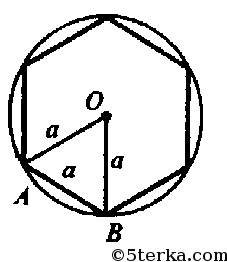
в) n=6. Обозначим сторону 6-угольника за х, следовательно, r=х.

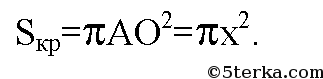
г) обозначим сторону правильного вписанного n-угольника за х. Следовательно, радиус описанной окружности равен

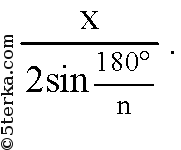
(Правильный n-угольник разбивается радиусами, проведенными из центра, на n одинаковых треугольников; все треугольники равновелики)

Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №671
к главе «Глава VII. Объемы тел. § 2. Объём прямой призмы и цилиндра».

Видео:Задание №671 — ГДЗ по геометрии 11 класс (Атанасян Л.С.)Скачать

671. В цилиндр вписана правильная n-угольная призма. Найдите отношение объемов призмы и цилиндра, если: а) n = 3; б) n = 4; в) n=6; г) n = 8; д) n произвольное целое число

Глава VII. Объемы тел. § 2. Объём прямой призмы и цилиндра → номер 671

Очевидно, что высота призмы равна высоте цилиндра. Тогда отношение объемов равно отношению площадей оснований призмы и цилиндр.

А) n=3, ΔАВС — правильный. Обозначим сторону ΔАВС равной х, следовательно,

Б) n=4, ABCD — квадрат. Обозначим сторону квадрата равной х.

Читайте также: Цилиндр гидравлический с насосом t01208 ae t 8т двойной

В) n=6. Обозначим сторону 6-угольника за х, следовательно, r=х.

Г) обозначим сторону правильного вписанного n-угольника за х. Следовательно, радиус описанной окружности равен

Видео:Задание № 671 — Геометрия 8 класс (Атанасян)Скачать

671 в цилиндр вписана

Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

В куб вписан шар радиуса 1. Найдите объем куба.

В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.

Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.

Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.

Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.

Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на

Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на

Около куба с ребром описан шар. Найдите объем этого шара, деленный на

Вершина A куба с ребром 1,6 является центром сферы, проходящей через точку A₁. Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину

Читайте также: Тормозной цилиндр задний 2101 или 2105

Видео:Задание №672 — ГДЗ по геометрии 11 класс (Атанасян Л.С.)Скачать

671 в цилиндр вписана

Примечание. Это часть урока с задачами по геометрии (раздел стереометрия). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение.

Видео:Призма и цилиндр. Практическая часть. 11 класс.Скачать

Задача. Призма, вписанная в цилиндр

В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 60 градусам. Диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 45 градусов. Найдите объем цилиндра.

Решение .
Объем цилиндра найдем по формуле:

где:
R — радиус основания прямого цилиндра,
h — высота.

Найдем основание цилиндра. 1-й способ .
Основание цилиндра одновременно является окружностью, описанной вокруг прямоугольного треугольника, являющегося основанием призмы. Диаметр окружности, описанной вокруг прямоугольного треугольника, лежит на его гипотенузе. То есть длина гипотенузы равна 2R.

Радиус окружности, описанной вокруг треугольника найдем по формуле:

R = x / 2 sin α
где:
x — сторона треугольника
α — угол, противолежащий стороне а.

Противолежащий угол найдем следующим образом. Поскольку треугольник прямоугольный, то противолежащий катету угол будет равен 180-90-60 = 30 градусов. Таким образом, радиус описанной окружности (он же радиус цилиндра) равен:

Найдем основание цилиндра. 2-й способ
У прямоугольного треугольника гипотенуза одновременно является диаметром описанной окружности. Половина гипотенузы будет равна ее радиусу.
Таким образом найдем гипотенузу для прямоугольного треугольника, зная угол и его катет через тригонометрическую функцию:
2R = 2a / cos 60 = 2a / 0.5 = 4a
R = 2a

Найдем высоту цилиндра .
Диаметр описанной окружности образует с диагональю призмы прямоугольный треугольник, один катет которого является диаметром описанной окружности, второй — высотой цилиндра и призмы, а гипотенуза является диагональю большей стороны призмы и одновременно цилиндра.

Поскольку угол диагонали с основанием составляет 45 градусов, то второй угол равен 180 — 45 — 90 = 45 градусов.
Исходя из того, что прямоугольный треугольник равнобедренный, то высота цилиндра и призмы равна диаметру окружности. Таким образом:

V = пR 2 h
V = п*4a 2 *4a
V = п16a 3 .

Видео:№671. Через точку А проведены касательная АВ (В — точка касания) и секущая, которая пересекаетСкачать

Задача. В цилиндр вписана правильная шестиугольная призма

В цилиндр вписана правильная шестиугольная призма. Найти угол между диагональю ее боковой грани и осью цилиндра, если радиус основания равен высоте цилиндра.

Если радиус основания равен высоте цилиндра, диагональ боковой грани правильной шестиугольной призмы представляет собой прямоугольный треугольник, у которого один из катетов равен высоте цилиндра (r), а второй катет равен стороне шестиугольника, вписанного в окружность.Согласно свойствам шестиугольника, вписанного в окружность, его сторона равна радиусу такой окружности.

То есть, каждая боковая грань данной вписанной призмы – квадрат. Диагональ грани образует с осью цилиндра, как и с боковым ребром, одинаковый угол 45°, так как ось цилиндра и боковые ребра вписанной призмы параллельны.

Видео:11 класс, 25 урок, Сфера, вписанная в цилиндрическую поверхностьСкачать

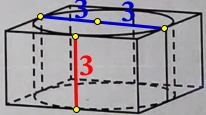
Решение №2305 Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3.

Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3. Найдите площадь боковой поверхности призмы.

Источник: Ященко ЕГЭ 2022 (36 вар)

Правильной четырёхугольной призмой – называется шестигранник, в основаниях которого находятся 2 квадрата, а боковые грани представлены прямоугольниками.
Площадь боковой поверхности данной призмы – это площадь 4-х равных прямоугольников.
Длина прямоугольника равна диаметру цилиндра, ширина прямоугольника равна высоте цилиндра.