а) Докажите, что площадь боковой поверхности цилиндра равна площади его основания.
б) Найдите площадь сечения цилиндра плоскостью, проходящей параллельно оси цилиндра на расстоянии 6 от неё.
а) Вспомним, что площадь боковой поверхности цилиндра вычисляется по формуле , где — радиус основания, — высота цилиндра. В данном случае , поэтому , откуда и следует требуемое.
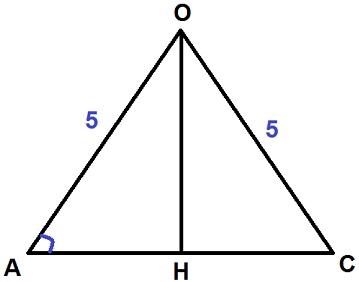
б) Сечение цилиндра плоскостью, проходящей параллельно его оси OO1, — прямоугольник ABB1A1 (O и AB — соответственно центр и хорда нижнего основания цилиндра), AA1 = 5. Расстояние от оси цилиндра до плоскости сечения равно высоте OH треугольника OAB. OA = OB = 10, OH = 6, откуда
В условии сказано, что дан цилиндр: «Высота цилиндра. «, а в решении рассмотрен прямой цилиндр. Действительно, ответ такой же получится при решении задачи с наклонным цилиндром, но тем не менее, в сечении образуется параллелограмм, а не прямоугольник: прямая АА1 параллельна и равна прямой ВВ1, как образующие, которые параллельны, в свою очередь оси цилиндра — прямой ОО1. По признаку параллельности прямой и плоскости получаем, что ОО1 параллельна плоскости (АА1ВВ1). И уже нельзя говорить, что ОО1 является высотой, ведь цилиндр может быть и наклонным. Прямая ОО1 является осью цилиндра. А условная прямая О1М может являться высотой цилиндра (точка М может совпасть с точкой О, если цилиндр прямой). Она будет являться и высотой параллелограмма (это может быть и прямоугольник, который по определению также является параллелограммом).
Таким образом, ответ хотя и верный, но рассмотрено частное решение данной задачи. Либо составители допустили ошибку не указав, что дан прямой цилиндр (в 2018-ом же писали: «. образующая перпендикулярна плоскости основания»), либо решение данной задачи следует подправить.
В школьном курсе задачи о наклонных цилиндрах не рассматриваются.
- Решение №1063 Радиус основания цилиндра равен 5, а высота равна 8.
- А прямом цилиндре радиус основания равен 5
- Решение
- Ответ
- Источники и прецеденты использования
- А прямом цилиндре радиус основания равен 5
- Решение №1063 Радиус основания цилиндра равен 5, а высота равна 8.
- А прямом цилиндре радиус основания равен 5
- 📽️ Видео
Видео:Радиус основания цилиндра равен 26, а его образующая равна 9... Найдите площадь сечения.Скачать

Решение №1063 Радиус основания цилиндра равен 5, а высота равна 8.
Радиус основания цилиндра равен 5, а высота равна 8. Отрезки AB и CD диаметры одного из оснований цилиндра, а отрезок AA1 его образующая. Найдите косинус угла между прямыми A1C и BD, если синус угла CAB равен 0,8.
Читайте также: Замена пыльников тормозных цилиндров ховер
Рассмотрим ΔАСО и ΔDBO, в них стороны AO = OC = OD = OB, как радиусы, углы при вершине О равны как вертикальные. Значит треугольники равны по углу и двум сторонам.
Тогда ∠СAO = ∠DBO, они внутренне накрест лежащие, тогда AC || BD.
По условию надо найти синус угла между прямыми A1C и BD, параллельным переносом перенесём BD на прямую АС и найдём угол АСА1.
Рассмотрим ΔАСА1:
Получаем ΔАОН египетский со сторонами 5, 4 и 3. AH = 3 (или по теореме Пифагора). Тогда AC:
AC = 2·AH = 2·3 = 6
Найдём в прямоугольном треугольнике АСА1 сторону А1С по теореме Пифагора:
А1С 2 = АА1 2 + АС 2
А1С 2 = 8 2 + 6 2 = 64 + 36 = 100
А1С = √100 = 10
Найдём косинус угла между прямыми A1C и BD:
Видео:№529. Высота цилиндра равна 8 см, радиус равен 5 см. Найдите площадь сечения цилиндраСкачать

А прямом цилиндре радиус основания равен 5
Радиус основания цилиндра равен равен r , а высота равна 5r . Около цилиндра описан параллелепипед, отношение объёма которого к объёму цилиндра равно . Найдите длину отрезка большей диагонали параллелепипеда, лежащего внутри цилиндра.
Решение
Пусть параллелепипед ABCDA 1B 1C 1D 1 описан около цилиндра (рис.1). Тогда параллелепипед – прямой, окружность одного основания цилиндра вписана в основание ABCD параллелепипеда, а окружность второго основания – в основание A 1B 1C 1D 1 . Поскольку в параллелограммы ABCD и A 1B 1C 1D 1 вписаны окружности, эти параллелограммы – ромбы. Если AC и A 1C 1 – большие диагонали этих ромбов, то AC 1 и A 1C – большие диагонали параллелепипеда. Поскольку высоты цилиндра и параллелепипеда равны, площади оснований параллелепипеда и цилиндра относятся как их объемы, а т.к. радиус окружности, вписанной в ромб, равен r , то площадь ромба равна его полупериметру, умноженному на r . Если a – сторона ромба, то
= = ,
откуда находим, что a = r . Пусть окружность с центром O , вписанная в ромб ABCD , касается стороны AB в точке F , а K – середина AB (рис.2). Обозначим OKB = α . Тогда
sin α = = = , cos α = ,
sin OAB = sin = = ,
поэтому
OA = = r , AC = 2OA = 2r ,
tg CAC 1 = = = , cos CAC 1 = .
Рассмотрим плоскость ACC 1A 1 (рис.3). Центры O и O 1 окружностей, вписанных в ромбы ABCD и A 1B 1C 1D 1 , – середины сторон AC и A 1C 1 прямоугольника ACC 1A 1 . Пусть M и N – точки пересечения первой окружности с отрезком AC , а M 1 и N 1 – второй окружности с отрезком A 1C 1 , причём MM 1 || NN 1 . Пусть диагональ AC 1 пересекает отрезки MM 1 и NN 1 в точках P и Q соответственно. Опустим перпендикуляр PH из точки P на NN 1 . Тогда
PQ = = = = 3r.
Читайте также: Объем параллелепипеда больше объема цилиндра в
Ответ
Источники и прецеденты использования
Проект осуществляется при поддержке и .
Видео:Геометрия Концы отрезка AB лежат на окружностях оснований цилиндра. Радиус основания равен 5 смСкачать

А прямом цилиндре радиус основания равен 5
Высота цилиндра равна 5, а радиус основания 10.
а) Докажите, что площадь боковой поверхности цилиндра равна площади его основания.
б) Найдите площадь сечения цилиндра плоскостью, проходящей параллельно оси цилиндра на расстоянии 6 от неё.
а) Вспомним, что площадь боковой поверхности цилиндра вычисляется по формуле , где — радиус основания, — высота цилиндра. В данном случае , поэтому , откуда и следует требуемое.
б) Сечение цилиндра плоскостью, проходящей параллельно его оси OO1, — прямоугольник ABB1A1 (O и AB — соответственно центр и хорда нижнего основания цилиндра), AA1 = 5. Расстояние от оси цилиндра до плоскости сечения равно высоте OH треугольника OAB. OA = OB = 10, OH = 6, откуда
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 2 |
| Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено, или при правильном ответе решение недостаточно обосновано. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
В условии сказано, что дан цилиндр: «Высота цилиндра. «, а в решении рассмотрен прямой цилиндр. Действительно, ответ такой же получится при решении задачи с наклонным цилиндром, но тем не менее, в сечении образуется параллелограмм, а не прямоугольник: прямая АА1 параллельна и равна прямой ВВ1, как образующие, которые параллельны, в свою очередь оси цилиндра — прямой ОО1. По признаку параллельности прямой и плоскости получаем, что ОО1 параллельна плоскости (АА1ВВ1). И уже нельзя говорить, что ОО1 является высотой, ведь цилиндр может быть и наклонным. Прямая ОО1 является осью цилиндра. А условная прямая О1М может являться высотой цилиндра (точка М может совпасть с точкой О, если цилиндр прямой). Она будет являться и высотой параллелограмма (это может быть и прямоугольник, который по определению также является параллелограммом).
Таким образом, ответ хотя и верный, но рассмотрено частное решение данной задачи. Либо составители допустили ошибку не указав, что дан прямой цилиндр (в 2018-ом же писали: «. образующая перпендикулярна плоскости основания»), либо решение данной задачи следует подправить.
В школьном курсе задачи о наклонных цилиндрах не рассматриваются.
Видео:№527. Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус цилиндра равен г,Скачать
Решение №1063 Радиус основания цилиндра равен 5, а высота равна 8.
Радиус основания цилиндра равен 5, а высота равна 8. Отрезки AB и CD диаметры одного из оснований цилиндра, а отрезок AA1 его образующая. Найдите косинус угла между прямыми A1C и BD, если синус угла CAB равен 0,8.
Читайте также: Значение детонации цилиндра рено логан
Рассмотрим ΔАСО и ΔDBO, в них стороны AO = OC = OD = OB, как радиусы, углы при вершине О равны как вертикальные. Значит треугольники равны по углу и двум сторонам.
Тогда ∠СAO = ∠DBO, они внутренне накрест лежащие, тогда AC || BD.
По условию надо найти синус угла между прямыми A1C и BD, параллельным переносом перенесём BD на прямую АС и найдём угол АСА1.
Рассмотрим ΔАСА1:
Получаем ΔАОН египетский со сторонами 5, 4 и 3. AH = 3 (или по теореме Пифагора). Тогда AC:
AC = 2·AH = 2·3 = 6
Найдём в прямоугольном треугольнике АСА1 сторону А1С по теореме Пифагора:
А1С 2 = АА1 2 + АС 2
А1С 2 = 8 2 + 6 2 = 64 + 36 = 100
А1С = √100 = 10
Найдём косинус угла между прямыми A1C и BD:
Видео:🔴 Радиус основания цилиндра равен 15, а его ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

А прямом цилиндре радиус основания равен 5
Высота цилиндра равна 3, а радиус основания равен 13.
а) Постройте сечение цилиндра плоскостью, проходящей параллельно оси цилиндра, так, чтобы площадь этого сечения равнялась 72.
б) Найдите расстояние от плоскости сечения до центра основания цилиндра.
а) Пусть OO1 — ось цилиндра. Проведем AB и CD параллельно оси цилиндра. Проведем BD и AC. Так как через две параллельные прямые проходит единственная плоскость, то прямоугольник BDCA — искомое сечение (см. рис.).
б) В этом прямоугольнике одна сторона будет равняться высоте цилиндра, а вторая — хорде окружности, лежащей в основании. Так как то где x — хорда AC. Проведем OH перпендикулярно AC. В силу того, что треугольник ACO равнобедренный, точка H также будет являться серединой AC. Тогда из прямоугольного треугольника, у которого гипотенуза — радиус OC, а один катет — половина этой хорды, находим второй катет OH по теореме Пифагора.
Таким образом, расстояние от центра окружности до сечения равно 5.
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
📽️ Видео
Радиус основания цилиндра равен 26. Найти площадь сеченияСкачать

№530. Высота цилиндра равна 12 см, а радиус основания равен 10 см. Цилиндр пересеченСкачать

ЕГЭ. Математика. База . Задача 16. Радиус основания цилиндра равен 26.Скачать

Видеоурок по математике "Цилиндр"Скачать

Геометрия Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4Скачать

11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

ЕГЭ 2022 математика задача 4 вариант 2Скачать

🔴 Даны два цилиндра. Радиус основания и высота ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Задание 2|ЕГЭ ПРОФИЛЬ| СТЕРЕОМЕТРИЯ| Цилиндр вписан в прямоугольный параллелепипед.Радиус основанияСкачать

🔴 Даны два цилиндра. Радиус основания и высота ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Стереометрия, номер 38.1Скачать

ЕГЭ по математике. Базовый уровень. Задание 16. Цилиндр. Площадь прямоугольника.Скачать

Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндраСкачать

ЗАДАНИЕ 8 из ЕГЭ_53Скачать

№538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевогоСкачать