Abcd прямоугольная пирамида вписанная в цилиндр

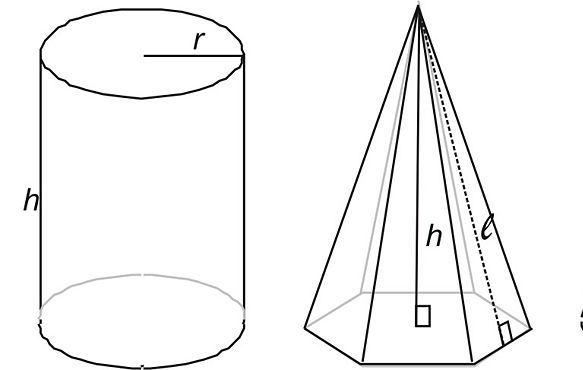
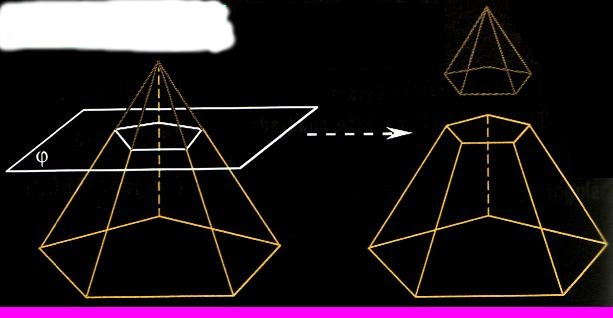
@ Тела вращения и многогранники могут быть вписаны одно в другое при некоторых ограничениях.

Призма называется вписанной в цилиндр , если ее основания – многоугольники, вписанные в окружности оснований цилиндра, а боковые ребра совпадают с образующими цилиндра.

В цилиндр можно вписать только такую прямую призму, основания которой можно вписать в окружность.

Призма называется описанной около цилиндра , если ее основания – многоугольники, описанные около окружностей оснований цилиндра.

Около цилиндра можно описать только такую прямую призму, основания которой – многоугольники, которые можно описать около окружности.

Очевидно, что у таких цилиндров и призм высоты равны.

Призма называется вписанной в конус , если одно ее основание вписано в окружность сечения конуса плоскостью, параллельной основанию, а другое основание принадлежит основанию конуса.

В конус можно вписать только такую прямую призму, вокруг основания которой можно описать окружность.

Очевидно, что высота вписанной призмы меньше высоты конуса.

Конус называется вписанным в прямую призму , если его вершина принадлежит одному основанию призмы, а основание конуса вписано в другое основание призмы.

Конус можно вписать только в такую призму, в основание которой можно вписать окружность.

Очевидно, что в этом случае высота конуса и высота призмы равны.

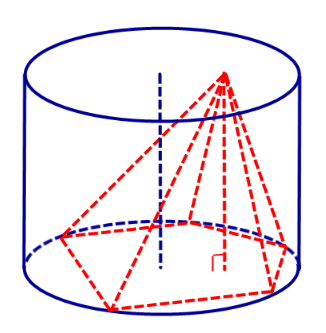
Пирамида называется вписанной в конус , если ее ребра совпадают с образующими конуса, а основание вписано в основание конуса.

Попробуйте доказать утверждение

Для того, чтобы в конус можно было вписать пирамиду, необходимо и достаточно, чтобы у нее были равные боковые ребра.

Конус называется вписанным в пирамиду , если его вершина совпадает с вершиной пирамиды, а основание вписано в основание пирамиды.

В пирамиду можно вписать конус тогда и только тогда, когда все апофемы боковых граней пирамиды равны.

Очевидно, что у таких конусов и пирамид высоты равны.

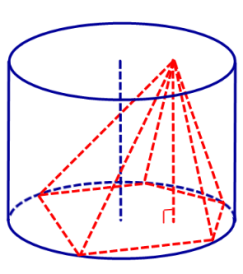
Пирамида называется вписанной в цилиндр , если ее вершина принадлежит одному основанию цилиндра, а основание вписано в другое основание цилиндра.

В цилиндр можно вписать пирамиду, основание которой можно вписать в окружность.

Очевидно, что высота вписанной пирамиды равна высоте цилиндра.

Цилиндр называется вписанным в пирамиду , если одно его основание совпадает с окружностью вписанной в сечение пирамиды плоскостью, параллельной основанию, а другое основание принадлежит основанию пирамиды.

В сечении пирамиды плоскостью, параллельной основанию, получается многоугольник, подобный основанию пирамиды. Следовательно, в пирамиду можно вписать цилиндр только в том случае, если в основании пирамиды – многоугольник, в который можно вписать окружность.

Очевидно, что высота вписанного цилиндра меньше высоты пирамиды.

Многогранник называется вписанным в сферу (шар) , если все его вершины лежат на сфере. Такая сфера называется описанной около многогранника.

1. Для того, чтобы около пирамиды можно было описать сферу, необходимо и достаточно, чтобы около основания пирамиды можно было описать окружность.

2. Около любой правильной пирамиды можно описать сферу.

3. Для того, чтобы около призмы можно было описать сферу, необходимо и достаточно, чтобы призма была прямая и около ее основания можно было описать окружность.

4. Около любой правильной призмы можно описать сферу.

Сфера называется вписанной в многогранник (а многогранник – описанным около сферы), если она касается всех его граней.

Читайте также: Ate сцепление рабочий цилиндр сцепления

Полезно уметь доказывать следующие утверждения

1. В любую правильную пирамиду можно вписать сферу (шар).

2. Для того, чтобы в призму можно было вписать сферу, необходимо и достаточно, чтобы в перпендикулярное сечение призмы можно было вписать окружность и чтобы высота призмы была равна диаметру этой окружности.

3. В правильную призму можно вписать сферу тогда и только тогда, когда ее высота равна диаметру окружности, вписанной в основание.

1. Найти площадь основания правильной призмы, вписанной в цилиндр, радиус основания которого равен R .

Ответ: , где n – число сторон.

Очевидно, такой же ответ будет для правильной пирамиды, вписанной в конус.

2. В шар радиуса R вписана правильная четырехугольная пирамида с высотой, равной Н . Как связана сторона основания пирамиды с высотой пирамиды и радиусом шара?

Пример 7.7.2. (КубГУ, матем., 1971 г.).

В шар радиуса R вписана правильная треугольная пирамида с плоским углом a при вершине. Найти объем пирамиды, а также боковую поверхность конуса, описанного около указанной пирамиды. Решение

Высоту пирамиды найдем из прямоугольного треугольника AOD , .

DM – диаметр шара. Тогда в сечении шара, проходящем через диаметр DM и точку А , получим прямоугольный треугольник AMD . Из метрических соотношений в прямоугольном треугольнике имеем .

Тогда площадь основания найдем по формуле .

И из формулы находим объем пирамиды

Ребро AD по определению описанного конуса является его образующей. Тогда найдем боковую поверхность описанного конуса по формуле S бок = p r1. S бок .

Пример 7.7.3. (КубГУ, матем., 1979 г.)

В конус, образующая которого длины наклонена к плоскости основания под углом a , вписана правильная n -угольная призма, все ребра которой имеют равные длины. Найти полную поверхность призмы. Решение

По условию все ребра n — угольной призмы равны, следовательно, ее грани – квадраты. Пусть сторона квадрата равна a , тогда S бок , .

Пример 7.7.4. (КубГУ, матем., 1991 г.)

В силу равноудаленности точки О от вершин S, A, B, C, D следует, что OABCD – правильная четырехугольная пирамида.

Следовательно, треугольник SAD – равносторонний и OASD – правильная треугольная пирамида. Тогда точка О проектируется на грань SAD в центр треугольника SAD . Отсюда , .

Из треугольника SON находим искомый радиус SO

Видео:Видеоурок по математике "Цилиндр"Скачать

Пирамида, вписанная в цилиндр

Видео:Усеченная пирамида, вписанная в шар, или шар, описанный около усеченной пирамиды.Скачать

Пирамида, вписанная в цилиндр. Свойства пирамиды, вписанной в цилиндр

Определение 1. Пирамидой, вписанной в цилиндр, называют такую пирамиду, у которой основание вписано в одно из оснований цилиндра, а вершина лежит на другом основании цилиндра (рис. 1).

Определение 2. Если пирамида вписана в цилиндр, то цилиндр называют описанным около пирамиды.

Замечание. Если пирамида вписана в цилиндр, то высота пирамиды равна высоте цилиндра.

Из определения пирамиды, вписанной в цилиндр, легко вытекает следующее утверждение, доказательство которого мы оставляем читателю.

Утверждение. Около любой правильной пирамиды можно описать цилиндр.

Видео:10 класс, 32 урок, ПирамидаСкачать

Отношение объемов цилиндра и вписанной в него правильной n — угольной пирамиды

Задача. Найти отношение объемов цилиндра и вписанной в него правильной n — угольной пирамиды.

Решение. Поскольку объем цилиндра вычисляется по формуле

а объем пирамиды вычисляется по формуле

Поскольку площадь правильного n — угольника выражается через радиус R описанной около этого многоугольника окружности по формуле

Следствие 1. Отношение объема правильной треугольной пирамиды к объему цилиндра, описанного около данной пирамиды, равно

Следствие 2. Отношение объема правильного тетраэдра к объему цилиндра, описанного около данного тетраэдра, равно

Следствие 3. Отношение объема правильной четырехугольной пирамиды к объему цилиндра, описанного около данной пирамиды, равно

Следствие 4. Отношение объема правильной шестиугольной пирамиды к объему цилиндра, описанного около данной пирамиды, равно

Видео:9 Пересечение 5 ти гранная пирамида минус цилиндрСкачать

Вписанный в пирамиду цилиндр. Цилиндр и пирамида: варианты комбинаций

Одними из интересных задач, которые позволяют сравнить различные объемные фигуры, являются задачи на описание одной из них около другой. В данной статье рассмотрим различные варианты описанного около пирамиды и вписанного в пирамиду цилиндра.

Видео:10 класс, 33 урок, Правильная пирамидаСкачать

Пирамида в геометрии

Прежде чем изучать комбинации вписанного в пирамиду цилиндра и вписанной пирамиды в цилиндр, следует рассмотреть эти фигуры с точки зрения геометрии. Начнем с пирамиды.

Фигура пирамида представляет собой тело в пространстве, которое получается, если соединить все вершины произвольного плоского n-угольника с некоторой точкой в пространстве. При этом n-угольник может быть совершенно произвольным (выпуклым, вогнутым, правильным, с различным количеством сторон n). На положение отмеченной точки накладывается одно единственное условие: она не должна лежать в той плоскости, в которой n-угольник находится.

На рисунке выше показана, пожалуй, самая известная пирамида — четырехугольная. Видно, что вершины четырехугольника, который называется основанием фигуры, соединены с точкой, лежащей над ним. Эта точка называется вершиной пирамиды.

Приведенное определение и также представленный рисунок свидетельствуют, что любая пирамида, независимо от типа ее основания, будет включать в себя n треугольников. Все они соединяются в вершине фигуры.

Перпендикулярный отрезок, проведенный из вершины фигуры к ее основанию, называется высотой. Если высота пересекает в геометрическом центре n-угольник, то такая пирамида будет прямой. В противном случае имеет место наклонная фигура.

Если все стороны n-угольника равны между собой, и фигура является прямой, то ее называют правильной. Именно с правильными пирамидами удобно работать при изучении их взаимного расположения с другими объемными телами в геометрии.

Видео:Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

Цилиндр в геометрии

Цилиндр в общем случае можно получить, если вдоль замкнутой кривой перемещать отрезок параллельно самому себе таким образом, чтобы отрезок не лежал в плоскости этой кривой. Этот отрезок называется образующей цилиндра, а кривая, вдоль которой он перемещается, носит название направляющей.

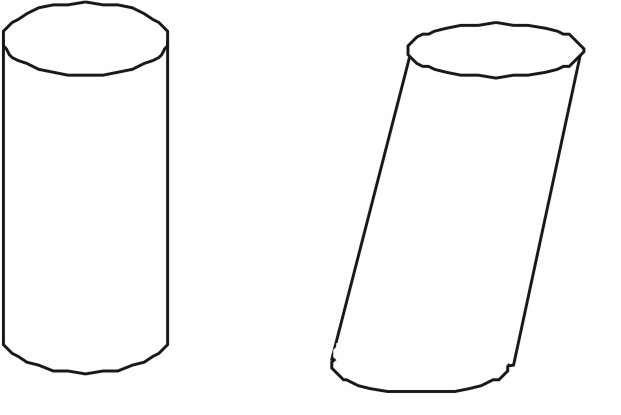
Если направляющая является окружностью, а образующая ей перпендикулярна, то полученный цилиндр будет называться прямым с круглым основанием. Эта фигура известна каждому. Она представлена на рисунке ниже.

Далее будем рассматривать только прямой круглый цилиндр.

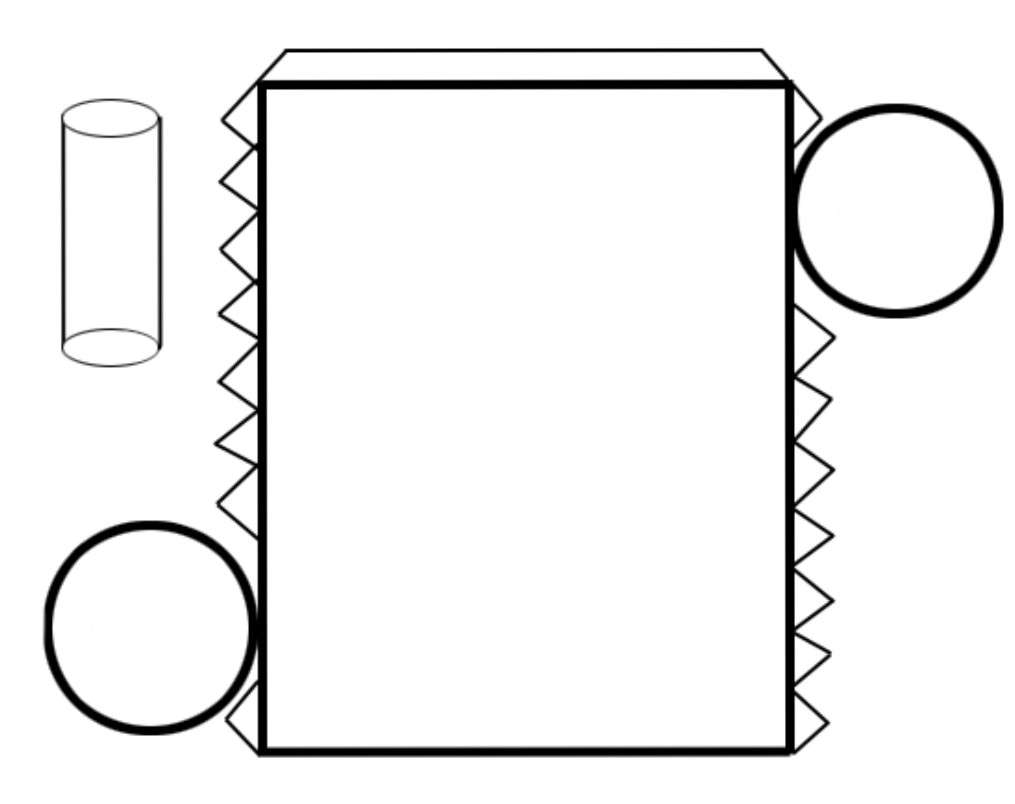
В отличие от пирамиды, цилиндр не имеет вершин и ребер. Однако он образован двумя основаниями (два одинаковых круга, находящихся в параллельных плоскостях) и боковой цилиндрической поверхностью. Если посмотреть на развертку этой фигуры, то можно увидеть, что она состоит из двух кругов и одного прямоугольника (см. рис. ниже).

Основными характеристиками цилиндра являются следующие:

• радиус основания;
• высота — расстояние между основаниями;
• площадь оснований и боковой поверхности;
• объем фигуры.

Видео:Пирамида, вписанная в конус.Скачать

Многоугольник и окружность

Последний вопрос, который следует изучить перед тем, как рассматривать вписанный в пирамиду цилиндр и описанный около нее, связан с взаимным расположением правильного многоугольника и окружности.

Существуют всего два варианта расположения этих плоских фигур:

• описание окружностью n-угольника;
• описание n-угольником окружности.

Приведем формулы, позволяющие вычислить длину стороны многоугольника через радиус окружности. Рассмотрим для примера только два первых многоугольника, то есть равносторонний треугольник и квадрат.

Если окружность проходит через все вершины n-угольника, то говорят, что она его описывает. При известном радиусе R длина стороны вычисляется по формуле:

То есть сторона квадрата, вписанного в окружность с радиусом R, будет немного меньше таковой для равностороннего треугольника, описанного той же окружностью.

Если окружность касается каждой из сторон n-угольника, то говорят, что она вписана в него. В случае правильных многоугольников точка касания фигур находится точно посередине каждой стороны n-угольника. Если известен радиус r окружности вписанной, тогда сторона n-угольника определится по формуле:

То есть вокруг окружности фиксированного радиуса можно описать треугольник с большей длиной стороны, чем квадрат.

Видео:Призма и пирамида. Площадь и объем. Вебинар | Математика 10 классСкачать

Треугольная пирамида, вписанная в цилиндр

Сначала рассмотрим более простой вариант, то есть когда пирамида находится внутри цилиндра. Разберем конкретный пример с правильной треугольной пирамидой. Предположим, что известен радиус R цилиндра и его высота h. Необходимо найти характеристики правильной треугольной пирамиды, вписанной в цилиндр.

Выше уже была приведена формула для стороны равностороннего треугольника, находящегося внутри окружности. Длина его стороны является длиной основания пирамиды. Она равна:

Вершина пирамиды вписанной лежит точно в центре верхнего основания цилиндра, поэтому высоты обеих фигур равны.

Зная длину стороны основания и высоту правильной пирамиды треугольной, можно рассчитать другие ее характеристики. Например, объем вычисляется по формуле:

Длину бокового ребра ab можно рассчитать так:

Видео:ЕГЭ|Задание 3 - Цилиндр, конус и шарСкачать

Пирамида четырехугольная, вписанная в цилиндр

Как и в предыдущем случае, пирамида находится внутри цилиндра. Только теперь ее основание представляет собой квадрат, сторона которого через радиус R цилиндра вычисляется так:

Высота пирамиды равна таковой для цилиндра, то есть h.

Объем правильной четырехугольной пирамиды (вписана в цилиндр), равен:

Длина бокового ребра ab составляет:

Заметим, что формула для длины бокового ребра получилась точно такой же, как в случае треугольной пирамиды.

Видео:ЕГЭ. Задача 8. Призма и цилиндрСкачать

Цилиндр вписан в фигуру

Цилиндр, вписанный в пирамиду, представляет более сложный случай расположения этих фигур. Чтобы рассчитать размеры пирамиды по известному радиусу и высоте цилиндра, следует разобраться, как этот цилиндр будет расположен внутри нее.

Предположим, что имеется плоскость, параллельная основанию пирамиды. Пересечем этой плоскостью боковую поверхность фигуры. Образованное сечение будет представлять точно такой же многоугольник, что лежит в основании, но меньшего размера. Этот многоугольник будет описывать верхнее основание цилиндра. Нижнее основание будет лежать в основании пирамиды.

Чтобы найти длину стороны многоугольника сечения, следует воспользоваться функцией зависимости площади сечения от вертикальной координаты z. Эта функция имеет вид:

Здесь z — расстояние от основания пирамиды вдоль ее высоты, hp — высота пирамиды.

Как пользоваться этой формулой для определения параметров описанной около цилиндра пирамиды, покажем на примере решения задачи.

Видео:13.04.23, 11 егэ стереометрия, призма, пирамида, параллелепипед, цилиндр, сфера, шар, сечения,объемыСкачать

Задача с четырехугольной пирамидой и цилиндром

Известно, что цилиндр имеет радиус r = 5 см и высоту h = 6 см. Найти высоту и сторону правильной четырехугольной пирамиды, описывающей его.

Верхнее основание цилиндра должно вписываться в квадратный срез на высоте h = 6 см от основания пирамиды. Тогда площадь сечения равна:

Здесь a — сторона основания пирамиды. Если взять квадратный корень из S(6), то получим длину стороны квадрата сечения. Она должна быть равна 2*r, чтобы основание цилиндра могло вписаться в это сечение, тогда получаем:

Отсюда получаем выражение:

Таким образом, вписать цилиндр, заданный условием задачи, можно не в одну единственную правильную четырехугольную пирамиду, а в бесконечное их число. Однако параметры каждой из них должны удовлетворять выражению выше, которое связывает высоту фигуры с длиной стороны ее основания.

📽️ Видео

Тема 71. Геометрические тела: шар, куб, пирамида, призма, цилиндр, конусСкачать

ЕГЭ Задание 14 Пирамида вписана в сферуСкачать

Геометрия 10 класс (Урок№15 - Пирамида.)Скачать

Учимся дома. 11 класс. Геометрия: Решение задач на объемыСкачать

Быстро находим радиус описанной сферыСкачать

Пирамида, вписанная в шар, или, шар, описанный около пирамиды.Скачать

Призма и цилиндр. Практическая часть. 11 класс.Скачать