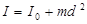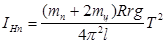- Момент инерции для чайников: определение, формулы, примеры решения задач
- Что такое инерция
- Определение момента инерции
- Теорема Штейнера
- Пример решения задачи на нахождение момента инерции
- Определение относительной погрешности при вычислении момента инерции цилиндра
- Лабораторная — Определение момента инерции твёрдых тел 2
- 🔥 Видео
Видео:Расчет момента инерции цилиндраСкачать

Момент инерции для чайников: определение, формулы, примеры решения задач
Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Видео:момент инерции цилиндраСкачать

Что такое инерция
Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.
Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».
Видео:Момент инерцииСкачать

Определение момента инерции
Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.
По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.
Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.
Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.
Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:
Видео:Урок 94. Вычисление моментов инерции телСкачать

Теорема Штейнера
От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.
Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Теорема Гюйгенса-Штейнера гласит:
Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.
Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:
Видео:Зависимость углового ускорения от момента инерцииСкачать

Пример решения задачи на нахождение момента инерции
Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.
Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:
Массу кольца можно представить в виде:
Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:
В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.
Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.
Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:
Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.
Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.
Видео:Расчет момента инерции диска или цельного цилиндраСкачать

Определение относительной погрешности при вычислении момента инерции цилиндра
Определение момента инерции цилиндра, если ось вращения проходит через центр масс (используются 2 цилиндра)
Читайте также: Расточка блока цилиндров в краснодарском крае
Проверка теоремы Штейнера
При переносе оси вращения или отдельных частей тела относительно этой оси его момент инерции изменяется. Соотношение между моментами инерции тела относительно некоторой оси вращения, проходящей через центр масс, и относительно произвольной, параллельной ей оси устанавливается с помощью теоремы Гюйгенса- Штейнера.
Рабочая формула:
mn – масса платформы (228 грамм)
R – радиус платформы (10 см)
mц – масса 1 цилиндра (745 гр)
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Видео:Момент инерции абсолютно твердого тела. 10 класс.Скачать

Лабораторная — Определение момента инерции твёрдых тел 2
Томский межвузовский центр дистанционного образования
Томский государственный университет систем управления и радиоэлектроники (ТУСУР)
Кафедра промышленной электроники (ПрЭ)
Лабораторная работа по курсу «Общая физика»
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЁРДЫХ ТЕЛ
Целью настоящей работы является определение момента инерции твердых тел и экспериментальная проверка справедливости теоремы Штейнера на примере физического маятника.
2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА
Для экспериментальной проверки теоремы Штейнера и определения момента инерции в данной работе используется стандартная установка универсального маятника ФПМО — 4. Это настольный прибор (рис. 4.1), на вертикальной стойке основания 1 которого крепится кронштейн 2, который имеет возможность поворота вокруг стойки на 360° и фиксация в любом выбранном положении. С одной стороны кронштейна 2 подвешен математический маятник, а с другой — физический. Математический маятник представляет собой металлический шарик 3 на бифилярном подвесе 4. Физический маятник — стальной стержень 5, подвешенный на опорной призме 6. Опорная призма 6 может перемещаться по всей длине стержня и фиксироваться в требуемом положении.
Стержень 5 имеет кольцевые проточки, которые служат для надежной фиксации опорных призм. Установка снабжена фотоэлектрическим датчиком 7, который закреплен на вертикальной стойке с помощью кронштейна 8 и имеет возможность перемещаться как вдоль, так и вокруг стойки и фиксироваться в любом положении. Датчик предназначен для выдачи сигналов на Миллисекундомер 9. Физический Миллисекундомер выполнен самостоятельным прибором с цифровой индикацией времени и количества полных периодов колебаний маятника.
3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ
Средняя величина периода колебаний маятника:
t — продолжительность колебаний;
n — число колебаний за время t .
Формула для экспериментального расчета момента инерции прямого тонкого стержня:
T — период колебаний маятника;
l — расстояние от центра масс до точки подвеса маятника;
g — Ускорение свободного падения.
Истинное значение величины t лежит в интервале tизм — s (t) ≤ t ≤ t изм + s (t) , где tизм – значение величины t , полученное при измерении, а величина s (t) – абсолютная погрешность измерения величины t . Это неравенство принято записывать в следующем виде.
s сис (t) – систематическая абсолютная погрешность.
Мерой точности результатов измерений является относительная погрешность. Формула для расчета погрешности косвенных измерений:
Класс точности прибора не указан, выбираем значение абсолютной погрешности ∆ l как половину цены деления (0,005 м).
Формула для теоретического расчета момента инерции прямого тонкого стержня длиной d и массой m относительно оси, перпендикулярной к стержню и проходящей через его середину:
Выражение теоремы Штейнера:
где, I0 –момент инерции относительно оси, проходящий через центр масс;
l – расстояние между осями.
Доверительный интервал для l 2 :
4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ.
Результаты прямых и косвенных измерений представлены в таблице.
| Номер опыта | N | t , c | T , c | l 2 , м 2 | I, кг×м 2 | Примечание |
| 1 | 15 | 19,087 | 1,272 | 0,0841 | 0,0417 | |
| 2 | 15 | 18,567 | 1,237 | 0,0625 | 0,0340 | |
| 3 | 15 | 18,166 | 1,211 | 0,0441 | 0,0274 | |
| 4 | 15 | 18,086 | 1,206 | 0,0289 | 0,0220 | |
| 5 | 15 | 18,527 | 1,235 | 0,0169 | 0,0176 | |
| 6 | 15 | 20,129 | 1,342 | 0,0081 | 0,0144 | |
| 7 | 15 | 25,056 | 1,670 | 0,0025 | 0,0124 |
На основании полученных опытных данных рассчитаем среднюю величину периода колебаний маятника по формуле (3.1) и результаты занесём в таблицу 1.
Исходя из опытных данных таблицы 1, зная массу маятника m и расстояние от центра масс до точки подвеса маятника l , вычислим по формуле (3.2) значение момента инерции маятника I .
Рассчитаем относительные погрешности оценки точности измерений, учитывая абсолютную погрешность замера времени колебаний σ( t ) = ±2мс, относительную погрешность определения массы δ( m ) =2% по формулам (3.3) — (3.13):
Рассчитаем относительную погрешность момента инерции по формуле (3.4)
Рассчитаем доверительный интервал σ( I ) для каждого значения момента инерции I по формуле (3.9) и результаты занесем в таблицу 2.
Читайте также: Порядок расположения цилиндров ваз 2114
Определим t , l 2 , I с учетом доверительных интервалов и результаты занесем в таблицу 2 для каждого значения.
Таблица доверительных интервалов.
| № измерения | l 2 — σ( l 2 ) | l 2 + σ( l 2 ) | σ( I ) | I — σ( I ) | I + σ( I ) |
| 1. | 0,0812 | 0,0870 | 0,0011 | 0,0406 | 0,0428 |
| 2. | 0,0600 | 0,0650 | 0,0009 | 0,0331 | 0,0349 |
| 3. | 0,0420 | 0,0462 | 0,0008 | 0,0267 | 0,0282 |
| 4. | 0,0273 | 0,0305 | 0,0008 | 0,0212 | 0,0228 |
| 5. | 0,0156 | 0,0182 | 0,0007 | 0,0169 | 0,0183 |
| 6. | 0,0072 | 0,0090 | 0,0008 | 0,0136 | 0,0152 |
| 7. | 0,0020 | 0,0030 | 0,0012 | 0,0112 | 0,0136 |
На основании полученных опытных и расчётных данных построим график зависимости момента инерции твёрдого тела I от квадрата расстояния l 2 , от оси вращения до центра масс. Проведём через экспериментальные точки и доверительные интервалы прямую линию, экспериментальной зависимости I = f (l 2 ).
Используя полученные данные, построим линеаризованный график этой зависимости в координатах I , l 2 , с учетом доверительных интервалов:
Рассчитаем коэффициенты a и b линеаризованного графика
методом наименьших квадратов:
| N | X | y | xy | x^2 | Y^2 |
| 1 | 0,0841 | 0,0417 | 0,003507 | 0,00707 | 0,00174 |
| 2 | 0,0625 | 0,0340 | 0,002125 | 0,00391 | 0,00116 |
| 3 | 0,0441 | 0,0274 | 0,001208 | 0,00194 | 0,00075 |
| 4 | 0,0289 | 0,0220 | 0,000636 | 0,00084 | 0,00048 |
| 5 | 0,0169 | 0,0176 | 0,0003 | 0,00029 | 0,00031 |
| 6 | 0,0081 | 0,0144 | 0,000116 | 0,00007 | 0,00021 |
| 7 | 0,0025 | 0,0124 | 3,1E-05 | 0,00001 | 0,00015 |
| 0,2471 | 0,1695 | 0,007923 | 0,01412 | 0,0048 |
Используя график линеаризованной зависимости I = f (l 2 ), изображённой на рис.4.1 определим собственный момент инерции I 0 относительно оси проходящей через его центр масс, что составило:
Произведём расчёт момента инерции прямого тонкого стержня длиной d относительно оси перпендикулярной стержню и проходящей через его середину по формуле (3.11):
Экспериментальное значение массы стержня определяем по коэффициенту наклона прямой, m=(0,0340 кг×м 2 – 0,0144 кг×м 2 )/(0,0625 м 2 – 0,0081м 2 )=0,0196 кг×м 2 /0,0544 м 2 =0,360 кг.
Анализ графика на рис.4.1. показывает, что через экспериментальные точки и доверительные интервалы можно провести прямую линию. Следовательно, зависимость I = f (l 2 ) является линейной, значит, зависимость момента инерции твёрдого тела от квадрата расстояния от оси вращения до центра масс подтверждена экспериментально.
Найденное значение момента инерции I 0 прямого тонкого стержня длиной d на графике и рассчитанное по формуле (3.11) совпадают.
В результате проделанной лабораторной работы мы определили момент инерции I 0 физического маятника относительно оси, проходящей через центр масс, и момент инерции относительно оси, не проходящий через центр его масс и проверили справедливость теоремы Штейнера на примере физического маятника.
6.1 Как формулируется понятия инерции материальной точки и твёрдого тела?
Внутреннее свойство тел сохранять состояние своего движения в отсутствии сил и реагировать на их действия изменением состояния движения, сопротивляясь этим изменениям, называют, в общем случае, инерционностью.
Количественной мерой воздействия на тело в каждый момент времени, изменяющего состояние его поступательного движения, является сила F . Равенство силы нулю означает неизменность состояния тела – движения или покоя. Протяженное во времени воздействие оценивается как произведение силы на время её действия F∆ t , называют эту меру действия импульсом силы.
Импульс силы и сила – причинные динамические характеристики по отношению к объекту их приложения. Импульс переменной во времени силы, приходящийся на бесконечно малый интервал времени dt , есть дифференциал импульса силы Fdt . Равенство нулю дифференциала предполагает постоянство импульса тела: при неизменной массе тела вектор скорости его поступательного движения и сонаправленный с ним вектор импульса будут оставаться неизменными по величине и направлению (F = 0, mv = const ).
История формирования понятий динамики твёрдого тела такова, что между характеристиками поступательного движения материальной точки и вращательного движения твёрдого тела имеет место определённая аналогия, вытекающая из общности материалистических представлений о причинах и следствиях. Так, центральное понятие динамики материальной точки действие (воздействие, взаимодействие), описываемое силой F и импульсом силы F∆ t , в динамике твёрдого тела дополнилось характеристиками: моментом силы M – мерой мгновенного (текущего) действия – и импульсом момента силы M∆ t – мерой протяжённого во времени действия. Момент силы, или вращательный момент, определяется как векторное произведение действующей на тело силы и радиус-вектора точки приложения этой силы относительно какой-либо выбранной (выделенной) точки: M = r * F, M = r * F * sin ( r , F ).
Действуя на тело продолжительное время, вращательный момент обуславливает изменение состояния движения тела. По аналогии с теорией движения материальной точки, в которой импульс силы, как причинный фактор, обуславливает следствие – приращения импульса тела, равное импульсу силы, — в динамике твёрдого тела импульс момента силы вызывает изменение момента импульса тела L (M * dt = dL ).
Читайте также: Цилиндр подъема кузова камаз 5511 схема сборки
6.2 В каких ситуациях применима теорема Штейнера?
Если известен момент инерции тела относительно любой оси, проходящей через центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера. Суть, которой состоит в применении формулы:
где l – расстояние между осью симметрии тела и осью вращения,
I 0 – момент инерции тела относительно оси симметрии.
Момент инерции I относительно произвольной оси равен сумме момента инерции I 0 относительно оси, параллельной данной и проходящей через центр масс тела и произведения массы тела m на квадрат расстояния l между осями:
6.4 Под действием какой силы совершается колебательное движение маятника?
Колебательные движения физического маятника совершаются под действием силы тяжести около неподвижной горизонтальной оси, не проходящей через его центр тяжести. Силу тяжести P = mg можно разложить на две составляющие, одна из которых P 2 уравновешивается реакцией подвеса. Под действием другой P1 маятник приходит в движение. На основании второго закона Ньютона для динамики вращательного движения запишем:
где M – момент вращающей силы;
Модуль составляющей силы P1 = P sin φ . Знак «минус» выбран потому, что действующая сила направлена в сторону, противоположную положительному направлению отклонения маятника.
6.5 Является ли момент инерции аддитивной величиной?
Момент импульса твёрдого тела складывается из моментов импульса составляющих его материальных точек, т.е. момент импульса – аддитивная величина. Момент импульса материальной точки относительно произвольной точки пространства называют векторное произведение радиус-вектора материальной точки в системе отсчёта выбранной точки:
6.6 Объяснить метод определения момента инерции с помощью физического маятника.
В основе определения момента инерции тел с помощью физического маятника лежит экспериментальная проверка справедливости теоремы Штейнера. Зная ускорение свободного падения g , массу m , экспериментально измерив длину l и определив период T можно вычислить момент инерции маятника. Зависимость I = f ( l ) , как следует из выражения I = I 0 + ml 2 нелинейная и график зависимости представляет собой возрастающую кривую, по виду которой нельзя утверждать о проверяемой зависимости.
Единственным графиком по виду, которого можно однозначно судить о характере исследуемой зависимости, является прямая линия, поэтому используем метод линеаризации. В данном случае такими переменными являются I и l 2 , следовательно, для проверки построим график I = f ( l 2 ) , при этом на него нанесём экспериментальные точки и доверительные интервалы. Через экспериментальные точки и доверительные интервалы (рис. 4.1) проводим прямую линию, т.е. экспериментальная зависимость [I = f ( l 2 ) ] момента инерции твёрдого тела от квадрата расстояния от оси вращения до центра масс является линейной, значит, правильность соотношения I = I 0 + ml 2 подтверждена экспериментально.
Используя график линеаризованной зависимости I = f ( l 2 ) можно вычислить массу стержня и собственный момент инерции, а также сравнить результаты расчёта и опыта.
Для этого сравним наше уравнение с уравнением прямой
где а – угловой коэффициент,
b – отрезок, отсекаемый прямой на оси y .
Угловой коэффициент определяется как
где ∆ x – приращение аргумента,
∆ y – соответствующее приращение функции.
6.7 Какой маятник называется физическим?
Физическим маятником называется любое твёрдое тело, которое под действием силы тяжести совершает колебания около неподвижной горизонтальной оси, не проходящей через центр масс.
Период Т малых колебаний физического маятника равен:
где I – момент инерции маятника относительно оси О ,
l – расстояние от точки A до оси О .
6.8 При каких формальных допущениях справедлива формула периода колебаний маятника (3.7)?
Собственные механические колебания возникают в физическом маятнике под действием силы тяжести вокруг неподвижной оси. Эти колебания в первом приближении не подвержены воздействию внешних сил. Модуль составляющей силы тяжести твёрдого тела определяется как P 1 = P * sin φ . При малых углах отклонения sinφ ≈ φ, а период колебаний не зависит от амплитуды колебаний. Поэтому формула периода колебания маятникаT = 2π ( I /( mgl )) 1/2 справедлива в случаях, когда угол отклонения маятника в положении равновесия мал и не должен превышать 5-10°.
6.9 Как записывается основной закон динамики вращательного движения?
Основное уравнение (закон) динамики вращательного движения: при воздействии момента внешних сил твёрдое тело вращается вокруг неподвижной оси с угловым ускорением, прямо пропорциональным моменту сил и обратно пропорциональным моменту инерции тела относительно данной оси:
где М – результирующий момент внешних сил, действующих на тело,
🔥 Видео
2 а Моменты инерции сферы и шараСкачать

Расчёт момента инерции тела относительно оси вращения. Момент инерции однородного стержняСкачать

5. Момент инерции простейших телСкачать

7. Момент инерции треугольника и конусаСкачать
Расчет момента инерции пластиныСкачать

Момент инерцииСкачать

Урок 98. Задачи на вычисление моментов инерции (ч.1)Скачать

Семинар №6 "Момент инерции. Уравнения моментов" (Чивилев В.И.)Скачать

ПОГРЕШНОСТЬ ИЗМЕРЕНИЯ 7 класс относительная абсолютная погрешностьСкачать

Относительная и абсолютная погрешностьСкачать

Погрешности измеренияСкачать

Определение моментов инерции твёрдых тел методом крутильных колебаний (лабораторная работа М30)Скачать

Момент инерции абсолютно твердого тела. Практическая часть. 10 класс.Скачать