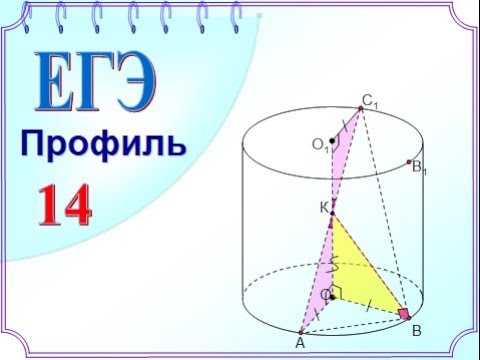
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В1 и С1, причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает ось цилиндра.
а) Докажите, что угол АВС1 прямой.
а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС1. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС1 — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.
Прямая СС1 является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна двум пересекающимся прямым, лежащим в плоскости ВСС1 (BС и СС1), а значит, прямая АВ перпендикулярна плоскости ВСС1 и любой прямой, лежащей в этой плоскости, в том числе и ВС1. Значит, угол АВС1 прямой.
б) Поскольку прямые ВВ1 и СС1 параллельны, искомый угол равен углу АС1С.
Треугольники АВС и АСС1 являются прямоугольными, поэтому:
Приведем другой способ решений.
a) Введем систему координат, как показано на рисунке. Найдем координаты точек A, B и C1. Пусть а радиус основания — r, тогда
Найдем координаты векторов и
Найдем скалярное произведение векторов и
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
Видео:Видеоурок по математике "Цилиндр"Скачать
Ac1 пересекает его ось цилиндра
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В1 и С1, причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает ось цилиндра.
а) Докажите, что угол АВС1 прямой.
а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС1. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС1 — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.
Прямая СС1 является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна двум пересекающимся прямым, лежащим в плоскости ВСС1 (BС и СС1), а значит, прямая АВ перпендикулярна плоскости ВСС1 и любой прямой, лежащей в этой плоскости, в том числе и ВС1. Значит, угол АВС1 прямой.
б) Поскольку прямые ВВ1 и СС1 параллельны, искомый угол равен углу АС1С.
Треугольники АВС и АСС1 являются прямоугольными, поэтому:
Приведем другой способ решений.
a) Введем систему координат, как показано на рисунке. Найдем координаты точек A, B и C1. Пусть а радиус основания — r, тогда
Найдем координаты векторов и
Найдем скалярное произведение векторов и
Видео:Задание 14 из реального ЕГЭСкачать
Ac1 пересекает его ось цилиндра
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В1 и С1, причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает ось цилиндра.
а) Докажите, что угол АВС1 прямой.
а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС1. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС1 — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.
Прямая СС1 является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна двум пересекающимся прямым, лежащим в плоскости ВСС1 (BС и СС1), а значит, прямая АВ перпендикулярна плоскости ВСС1 и любой прямой, лежащей в этой плоскости. Значит, угол АВС1 прямой.
б) Поскольку прямые ВВ1 и СС1 параллельны, искомый угол равен углу АС1С.
Треугольники АВС и АСС1 являются прямоугольными, поэтому:
Приведем другой способ решений.
a) Введем систему координат, как показано на рисунке. Найдем координаты точек A, B и C1. Пусть а радиус основания — r, тогда
Найдем координаты векторов и
Найдем длины векторов и
Найдем косинус угла между этими векторами:
Значит, угол АВС1 прямой.
Аналоги к заданию № 520803: 520853 520879 520915 Все
Видео:✓ Задача про цилиндр | ЕГЭ-2018. Задание 14. Математика. Профильный уровень | Борис ТрушинСкачать
Ac1 пересекает его ось цилиндра
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В1 и С1, причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает ось цилиндра.
а) Докажите, что угол АВС1 прямой.
б) Найдите площадь боковой поверхности цилиндра, если AB = 20, BB1 = 15, B1C1 = 21.
а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС1. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС1 — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.
Прямая СС1 является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна плоскости ВСС1б а значит, угол АВС1 прямой.
б) Отрезок AC является диаметром основания цилиндра. Значит, длина
окружности основания цилиндра равна
Следовательно, площадь боковой поверхности цилиндра равна
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
Видео:как ПРОЕЦИРОВАТЬ в Физике!Скачать
Ac1 пересекает его ось цилиндра
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В1 и С1, причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает ось цилиндра.
а) Докажите, что угол АВС1 прямой.
а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС1. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС1 — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.
Прямая СС1 является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна двум пересекающимся прямым, лежащим в плоскости ВСС1 (BС и СС1), а значит, прямая АВ перпендикулярна плоскости ВСС1 и любой прямой, лежащей в этой плоскости. Значит, угол АВС1 прямой.
б) Треугольник ABC1 прямоугольный, поэтому искомое расстояние равно его высоте h, проведённой к гипотенузе. Получаем:
Аналоги к заданию № 520803: 520853 520879 520915 Все
📸 Видео
Стереометрия из реального ЕГЭ. Конус и цилиндр. Вывезешь катку? | ЕГЭ по математике 2024 | СВСкачать
РТ_ПБ_61.1) Построить проекции линии пересечения цилиндра плоскостью частного положения.Скачать
ЕГЭ|Задание 14 - Цилиндр, конус и шарСкачать
Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать
5.1. Циклоалканы: Строение, изомерия. ЕГЭ по химииСкачать
ВАРИАНТ #16 ЕГЭ 2021 ФИПИ НА 100 БАЛЛОВ (МАТЕМАТИКА ПРОФИЛЬ)Скачать
РАЗБОР СЛИВА ЕГЭ 2024 | Ильич ЕГЭ 2024 Профильная Математика | СЛИВ ОТ ЯЩЕНКО |Скачать
РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать
ЦИЛИНДР геометрия егэ по математике профильный уровень ЯщенкоСкачать
Задача про ЦИЛИНДР / Как найти объем детали? / Профиль ЕГЭСкачать
11 класс, 15 урок, Площадь поверхности цилиндраСкачать
Задание 14 | ЕГЭ 2024 Математика (профиль) | Самые простые задачи по стереометрии из 2й частиСкачать
Цилиндр, конус и шар в задании 2 | Математика ЕГЭ 2023 | УмскулСкачать
✓ Задача, которая сломала Трушина | Комбинаторная геометрия | Ботай со мной #082 | Борис ТрушинСкачать
№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать
ЕГЭ Задание 14 Цилиндр Теорема о трёх перпендикулярахСкачать
