Акриловый цилиндр заряженный электронами

Кому Андрей Вознесенский посвятил самое известное свое стихотворение?

Встреча Андрея Вознесенского и Татьяны Лавровой положила начало их тайному роману.

Татьяна Лаврова — звезда фильма «Девять дней одного года», которая могла покорить любого мужчину одним только взглядом, к тому времени уже успела пережить два расставания после крушения отношений с Евгением Урбанским и Олегом Далем.

И кумир миллионов, поэт-шестидесятник Андрей Вознесенский, выступления которого собирали стадионы зрителей.

Вознесенский полностью завладел душой и сердцем актрисы. Их тайный роман, когда Лаврова ждала, что возлюбленный решится уйти из семьи, а он так и не осмелился поставить точку в отношениях с супругой — Зоей Богуславской, длился 7 лет и закончился болезненным расставанием.

Татьяне посвящено самое знаменитое стихотворение Андрея Вознесенского «Ты меня на рассвете разбудишь», ставшее сердцем рок-оперы Алексея Рыбникова «Юнона и Авось»

Ты меня на рассвете разбудишь,

проводить необутая выйдешь.

Ты меня никогда не забудешь.

Ты меня никогда не увидишь.

Заслонивши тебя от простуды,

Эту воду в мурашках запруды,

это Адмиралтейство и Биржу

Не мигают, слезятся от ветра

Возвращаться — плохая примета.

Даже если на землю вернемся

мы вторично, согласно Гафизу,

мы, конечно, с тобой разминемся.

И окажется так минимальным

перед будущим непониманьем

двух живых с пустотой неживою.

И качнется бессмысленной высью

пара фраз, залетевших отсюда:

Видео:Заполненный электронами акриловый цилиндрСкачать

ВЕРНОСТЬ!

Видео:Акриловый цилиндр заряженный электронамиСкачать

Черный красавец

Видео:Акриловые цилиндрыСкачать

Отсыпка фильтра в скважину

Видео:Что такое акрил (оргстекло)Скачать

Водородный взрыв

Видео:Акриловые цилиндры для вихревых колоннСкачать

Про радугу

Совсем немного о природе радуги

Видео:Молния в акрилеСкачать

Клетка-организм

Видео:Почему мы используем ПЭТ-пластик, а не акрил или оргстеклоСкачать

А вы знали что у выдрей есть специальный кармашек для хранения камня с помощью которого они открывают моллюсков?

Видео:Цирконий для ТВЭЛов. Семь раз отмерь — и на техконтрольСкачать

Про животных и вкусняшки

Видео:Главное свойство акрила о котором вы должны знать!Скачать

Вдогонку к посту «Прыгаем в чёрную дыру»

Бонусное видео с прыжком в чёрную дыру. Без комментариев и под атмосферное музыкальное сопровождение. Сделано в формате 360 градусов, так что можно покрутить и наблюдать от первого лица эффекты, описанные в основном видео с теорией.

Видео:Оргстекло - придание любой формы. DREMEL HOBBYСкачать

Прыгаем в чёрную дыру (ScienceCLic)

Как выглядит чёрная дыра? Какие оптические эффекты возникают в непосредственной близости от неё? Что мы увидим при пересечении горизонта событий?

Для визуализации использовались расчёты и симуляции.

Видео:ИЗГОТОВЛЕНИЕ ВЫСТАВОЧНЫХ СТЕНДОВ для Moscow Urban Forum 2016Скачать

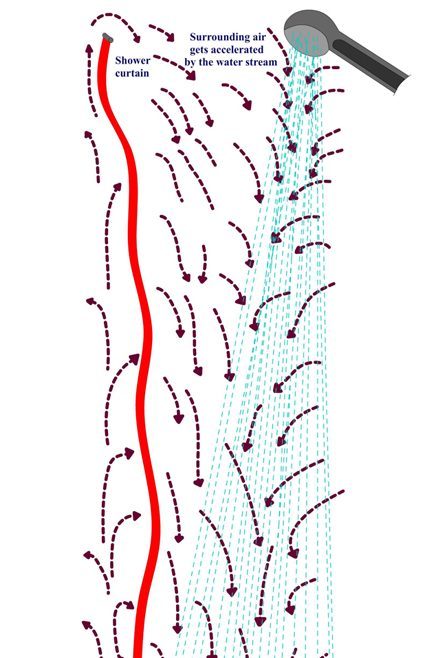
Почему занавеска в душе хочет к вам прилипнуть

31-летний профессор машиностроения Дэвид Шмидт из Университета Массачусетса в Амхерсте в 2001 году получил Шнобелевскую премию за то, что на софте за 28 000 долларов для моделирования потоков жидкостей просчитал модель, частично объясняющую, почему занавеска хочет прилипнуть к вам в душе. (Публикация в Scientific American )

Дэвид Шмидт исследовал способы точной имитации брызг и распыления (spray). Обычно они использовали эти симуляции распыления, чтобы помочь разработать лучшие дизельные и авиационные двигатели. Однако тот же анализ в равной степени применим и к душевой кабине в ванной. В конце концов, душ — это просто большая струя брызг.

В своей симуляции Дэвид Шмидт учел эффекты дробления капель, модель также учитывала деформацию (distortion) капель, которая существенно влияет на аэродинамическое сопротивление.

Все предыдущие объяснения были теоретические: от эффекта Бернулли (Bernoulli effect) до теории плавучести (buoyancy effect).

Гипотеза эффекта Бернулли

Самым популярным объяснением эффекта занавески для душа является принцип Бернулли. Принцип Бернулли гласит, что увеличение скорости приводит к снижению давления. Эта теория предполагает, что вода, вытекающая из насадки для душа, заставляет воздух, через который движется вода, течь в том же направлении, что и вода. Это движение будет параллельно плоскости занавески для душа. Согласно принципу Бернулли, если воздух движется по внутренней поверхности занавески для душа, давление воздуха там упадет. Это приведет к перепаду давления между внутренним и внешним пространством, что приведет к перемещению занавески внутрь. Эффект будет наиболее сильным, когда зазор между человеком и занавеской будет наименьшим, в результате чего занавеска будет прилипать к человеку.

Но эффект Бернулли основан на соотношении давления и ускорения и не учитывает наличия капель. И, по расчетам лауреата Шнобелевской премии, этот эффект не отвечает за прогиб занавески в душе.

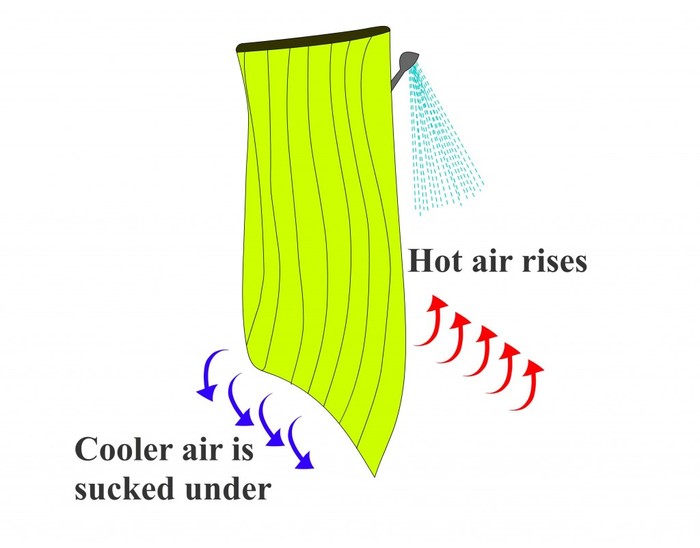
Также называемый эффектом дымохода или эффектом стека/тяги, подразумевает, что теплый воздух (из горячего душа) поднимается над занавеской душа, когда более прохладный воздух (около пола) проталкивается под занавеску, заменяя поднимающийся воздух. Если придвинуть занавеску к струе, вихрь (ближнего действия) и эффекты Коанда становятся более значительными. Однако эффект занавески для душа сохраняется при использовании холодной воды, что означает, что это не может быть единственным действующим механизмом.

Теория плавучести предполагает, что горячий душ вызывает повышение температуры воздуха в душе, уменьшая его плотность. В этом случае давление на душевой стороне занавески будет ниже, чем давление снаружи на той же высоте от пола, что приведет к смещению занавески в сторону более низкого давления. Проблема с этим объяснением состоит в том, что занавеска так же будет втягиваться внутрь к холодному душу.

Эффект Коанда, также известный как «прикрепление пограничного слоя», представляет собой тенденцию движущейся жидкости прилипать к соседней стене.

Видео:ОРГСТЕКЛО ИЛИ ОБЫЧНОЕ СТЕКЛО? КАКОЙ АКВАРИУМ ЛУЧШЕ? #АКВАМЕН #СВОИМИ_РУКАМИСкачать

Закрученный свет и закрученные электроны: обзор последних результатов

Видео:Лайфхак: собираем акриловый корпус.Скачать

Игорь Иванов

Рис. 1. Изображение из одной из статей про закрученный свет украсило обложку журнала Science за 19 октября 2012 года. Правда, такая картинка вряд ли объяснит, в чём, собственно, состоит закрученность света

За последние пару лет в разных, даже далеких от науки СМИ стали регулярно появляться новости про «закрученный свет». В подавляющем большинстве случаев эти новости воспринимаются скорее как новости технологии, поскольку они касаются лишь одного узкоспециального прикладного вопроса — увеличения информационной емкости световых импульсов или радиоволн за счет закрученности. Между тем, реальная физика закрученного света намного богаче, в ней есть разнообразные задачи как фундаментальной, так и практической физики. Кроме того, СМИ почти не пишут про закрученные электроны, а ведь эта тема сейчас не менее активна, чем закрученный свет. Мы попробуем здесь восполнить этот пробел, перечислив некоторые результаты, полученные за последние два-три года. Подборка эта, конечно, не охватывает все достижения и отражает предпочтения автора, но она должна дать общее представление о том, что сейчас вообще происходит в этой области.

Закрученный свет: введение

На самом простом уровне можно сказать, что закрученный свет — это световой пучок, который не просто летит вперед, но еще и крутится вокруг направления своего движения. Если свободно подвешенное тело будет поглощать такой свет, то оно реально начнет крутиться вокруг оси, совпадающей с направлением луча. Таким образом, этот световой луч передает телу не только энергию и импульс, но и вращательный момент импульса.

Если воспринимать слова «пучок закрученного света» слишком буквально, то сразу может возникнуть первое недопонимание. Ведь в любом вращающемся объекте действуют центробежные силы, и если объект от вращения не разваливается, то значит какие-то силы удерживают его части вместе. Но световой пучок состоит из фотонов. Неужели есть какие-то новые силы, которые удерживают фотоны друг рядом с другом, не дают им разлететься?! Нет, конечно. Такая мысленная картинка опирается на ошибочное представление о фотонах как об очень маленьких «комочках света», которые тесно упакованы внутри пучка. Но не будем забегать вперед; о том, как правильнее визуализировать закрученный свет в терминах отдельных фотонов будет рассказано чуть ниже. А пока вернемся к свету в рамках классической оптики.

Свет — это волна электромагнитного поля. Это поле находится сразу в большом объеме пространства, оно колеблется и, поддерживая себя само, распространяется вперед. Как и у всякой волны, у света есть волновой фронт — так называют воображаемую поверхность в пространстве, в точках которой световое колебание находится в какой-то конкретной фазе (то есть в каком-то конкретном положении после начала колебания). У обычной плоской волны все волновые фронты — плоскости, следующие друг за другом. У сферической волны волновые фронты — концентрические сферы. А у закрученного света волновой фронт геликоидальный (то есть винтовой, спиралеобразный); он словно наматывается винтом на направление распространения волны.

Закрученность света часто иллюстрируют картинкой наподобие рис. 2, слева. Тут всё верно, но, к сожалению, эта картинка часто сбивает с толку читателей, обладающих некоторыми познаниями в физике или технике. Дело в том, что очень похожие картинки используются для иллюстрации циркулярной поляризации света (рис. 2, внизу). В результате читатель, не слышавший раньше про закрученный свет, может подумать: «Опять всё журналисты перепутали, ведь это же обыкновенная циркулярная поляризация!»

Рис. 2. Вверху: три характеристики световой волны в зависимости от наличия и знака ее закрученности — волновой фронт (первая колонка), фаза волны в поперечной плоскости (вторая колонка), интенсивность света в фокусе (третья колонка); с сайта en.wikipedia.org.Внизу: спиралеобразная картинка, которой обычно иллюстрируют циркулярную поляризацию света; с сайта en.wikipedia.org

Поэтому сразу же подчеркнем: несмотря на визуальную схожесть картинок, закрученность и циркулярная поляризация — это два совершенно разных явления, две независимые степени свободы, которые вы можете «внедрить» в свет. Бывает свет с поляризацией, но без закрученности (это как раз обычный случай), бывают волны с закрученностью, но без поляризации (например, не свет, а акустические закрученные волны), бывают волны с тем и с другим, или же без того и без другого.

Разница тут вот в чем. Картинка с циркулярной поляризацией нарисована для плоской волны. Она показывает ориентацию электрического поля в разных точках вдоль луча. При этом считается, что эта ориентация одна и та же во всей поперечной плоскости. Картинка же с закрученным светом показывает не электрическое поле, а именно волновой фронт. Он не плоский, тут фаза волны меняется не только при движении вдоль луча, но и при смещении в поперечной плоскости (в первом ряду квадратиков на рис. 2 как раз показана цветом фаза в поперечной плоскости). Поскольку поток энергии световой волны обычно направлен перпендикулярно волновому фронту, то получается, что в закрученном свете энергия и импульс волны не просто летят вперед, а как бы крутятся при этом вокруг оси движения — отсюда и момент импульса. А вот вектор электрического поля для закрученного света обычно не рисуют, потому что это дополнительно усложняет картинку, да и набор возможностей тут становится намного богаче, чем для «плоского» света. Кстати, с одним простым примером необычной поляризации неплоского света читатели «Элементов» могли познакомиться в задаче Скорость радиально-поляризованного света.

Отметим, что в зависимости от того, в какую сторону поворачивается геликоид волнового фронта, закрученность бывает положительной и отрицательной — и в этом тоже есть сходство с поляризацией. Но, в отличие от поляризации, величина закрутки может быть, в принципе, сколь угодно большой; не просто +1 и –1, а +2, –5, +12 и т. д. В этом и заключается еще одна привлекательная черта закрученного света: у закрученности гораздо большая «информационная вместимость», чем у поляризации.

Вспомним теперь, что свет — это поток фотонов. С поляризацией тут всё понятно: известно, что каждый фотон несет какую-то поляризацию. А как обстоят дела с закрученностью? Оказывается, аналогично: каждый фотон в закрученном свете имеет ровно такой же спиральный волновой фронт. Вот она, та неправильность той наивной картинки, о которой говорилось в начале: тут каждый фотон занимает весь световой пучок, по крайней мере в поперечной плоскости, и причем простирается он в стороны достаточно далеко. Так что закрученность — это вовсе не коллективный эффект от большого числа фотонов, это индивидуальная характеристика, переносимая и на отдельные фотоны. Можно уменьшить яркость светового луча до такой степени, чтобы фотоны летели по одиночке, и всё равно закрученность при этом теряться не будет.

С точки зрения квантовой механики, поляризация фотона — это проявление его спина, а закрученность — это проявление орбитального углового момента фотона (значения m, приведенные на рис. 2, как раз отвечают проекции орбитального углового момента). И то, и другое — составляющие части полного момента импульса фотона, и они могут взаимодействовать друг с другом (спин-орбитальное взаимодействие внутри фотона). Поэтому возникает тонкий вопрос, связанный с тем, насколько вообще оправдано такое уверенное разделение спина и закрученности. Более того, этот вопрос выходит за пределы оптики, он обсуждается даже в современной физике элементарных частиц, в применении к кваркам и глюонам внутри протона. Мы здесь не касаемся этих вопросов; они слегка обсуждаются в заметке в блоге.

Закрученный свет: краткая история

О том, что световая волна несет не только энергию и импульс, но еще и угловой момент, было известно столетие назад. Поначалу, конечно, угловой момент ассоциировался только с поляризацией света, или, другими словами — как это выяснилось после создания квантовой теории излучения, — со спином фотонов. Но довольно быстро было понято, что фотоны могут нести и орбитальный угловой момент. В конце концов, когда электрон в атоме перепрыгивает с энергетического уровня с большим L в состояние с маленьким и излучает один фотон, то этот фотон просто обязан уносить какой-то орбитальный угловой момент, какое-то «вращение».

Это всё не вызывало никакого удивления и не ассоциировалось с каким-то «закрученным светом» — просто потому, что такие фотоны не летят в каком-то определенном направлении. Фотон, излученный возбужденным атомом, распространяется в виде расширяющейся волны сразу во все стороны. Когда такой фотон попадает в какое-то регистрирующее устройство или вызывает какой-то иной физический процесс, то он воздействует локально, лишь маленьким кусочком своего фронта — и тут же происходит квантовый коллапс световой волны, и от его «закрученности» не остается и следа.

Шло время. Были созданы лазеры, лазерным светом научились управлять, развивалась теория описания его электромагнитного поля. И в какой-то момент пришло осознание того, что эти два свойства — направленность светового пучка и его закрученность — вовсе не противоречат ни друг другу, ни строгому теоретическому утверждению квантовой теории о том, что спин и орбитальный момент нельзя абсолютно четко разделить для произвольного светового поля. Как оказалось, для узконаправленного лазерного луча — вполне можно. В пионерской статье 1992 года PRA 45, 8185 (1992) этот вопрос впервые был внимательно изучен. Помимо теории, в этой статье были предложены и конкретные схемы создания и детектирования закрученности.

Читайте также: Как улучшить прирабатываемость поршня в цилиндре

Три года спустя закрученный свет был получен экспериментально. Точнее, экспериментаторы убедились, что специальным образом приготовленная мода лазерного света, которую умели создавать и раньше, действительно отвечает закрученному свету. Сделали это изящно: в фокусе лазерного луча удалось «подвесить» микрочастицу. Поглощая свет, она начинала вращаться, и направление ее вращения зависело вовсе не от поляризации света, а от того, в какую сторону он был закручен.

После этого начался лавинообразный поток исследований закрученного света. Было разработано еще несколько методик получения фотонов с орбитальным угловым моментом (некоторые примеры см. в Википедии), простейший из которых можно реализовать чуть ли не в домашних условиях. Для этого вам потребуется взять хороший лазерный принтер и распечатать на прозрачке дифракционную решетку с дислокацией (рис. 3, слева) — но только, конечно, в сильно уменьшенном масштабе. После этого в центр решетки нужно посветить обычным лазерным лучом, правда с хорошей поперечной когерентностью. После прохождения решетки один луч расщепится на несколько — как и должно быть для всякой дифракционной решетки, — но только каждый лучик теперь будет нести свой определенный орбитальный угловой момент (рис. 3, справа).

Рис. 3. Слева: дифракционная решетка с дислокацией; с сайта hank.uoregon.edu. Справа: после прохождения такой решетки один луч расщепляется на несколько с разными состояниями закрученности; с сайта www.sciencemag.org

Параллельно с фундаментальными исследованиями начали развиваться и разнообразные применения закрученного света: в квантовой теории информации, в манипулировании микрочастицами и управлении микромашинами, в микроскопии, в астрофизике и т. д. Два года назад вышла даже книга, как раз посвященная самым разных применениям закрученного света (J. P. Torres, R. Torner, 2011. Twisted Photons). Все эти применения уже стали классическими, и потому мы опустим их детальное описание и перейдем к направлению исследования, которое сейчас только-только развивается.

Закрученные фотоны за пределами оптического диапазона

Рис. 4. Простейший прибор для излучения закрученных радиоволн. Изображение из статьи New J. Phys. 14, 033001 (2012)

Разумеется, для того чтобы быть закрученными, фотоны не обязаны принадлежать оптическому диапазону. Вопрос только в том, как эти закрученные фотоны за пределами оптического диапазона создать. Длинноволновое электромагнитное излучение, например радиоволны, создавать и закручивать несложно. Конечно, про отдельные фотоны тут речи уже не ведется, но для прикладных задач это несущественно. Например, в нашумевшей (даже в российских СМИ) статье New J. Phys. 14, 033001 (2012), в которой сообщалось об использовании закрученных радиоволн для передачи на одной несущей частоте сразу нескольких каналов (разновидность мультиплексирования), закручивание осуществлялось с помощью простейшего устройства — обычной параболической «тарелки», которую разрезали по радиусу, а затем отогнули кромки так, чтоб получился как раз один шаг спирали (рис. 4).

Длинные радиоволны тоже несложно закручивать — например, с помощью специально настроенных фаз и мощностей фазированной антенной решетки. Такие эксперименты делались на американской станции HAARP, которая занимается облучением ионосферы радиоволнами и наблюдением за возникающим из-за этого свечением. В 2009 году эта группа исследователей опубликовала статью PRL 102, 065004 (2009), в которой сообщается о накачке ионосферы радиоволнами с ненулевым орбитальным угловым моментом и наблюдением кольцеобразного свечения.

А вот уйти в другой конец спектра электромагнитных волн оказалось намного труднее. Стандартные методы закручивания тут уже не работают, и на это есть три причины. Во-первых, чем меньше длина волны, тем мельче должны быть детали той дифракционной решетки или иного устройства, преобразующего плоскую световую волну в закрученную. Во-вторых, все эти устройства должны быть сделаны из материала, который эффективно поглощает или отражает электромагнитные волны. Но для фотонов высокой энергии практически любое вещество становится прозрачным. И наконец, каково бы ни было это закручивающее устройство, падающая на него изначальная электромагнитная волна должна иметь достаточно большой участок ровного волнового фронта. Для фотонов высокой энергии добиться этого тоже непросто.

Тут стоит уточнить, что вообще хотят физики, когда говорят о создании закрученного света. Конечно, если вы возьмете узконаправленный луч рентгеновского излучения и просто как-то испортите его поперечный профиль, то плосковолновое излучение превратится в суперпозицию волн со всякими орбитальными угловыми моментами, то есть в том числе и в закрученные волны. Но проблема в том, что вы эти волны не разделите, не сможете получить чистый луч, несущий только определенный угловой момент. Именно получение такого луча и есть тут главная цель.

В этой ситуации наиболее перспективными кажутся попытки полностью изменить саму схему излучения закрученных фотонов. Например, в теоретической статье 2007 года было предложено использовать для этой цели спиральный ондулятор. Электронный сгусток высокой энергии не просто летит вперед в таком устройстве, а движется по спиральной траектории под действием магнитов. Из-за постоянного колебания из стороны в сторону электроны излучают электромагнитные волны, спектр которых можно поднять до рентгеновского диапазона. Как показали вычисления, из этого излучения можно извлечь и достаточно яркий пучок закрученного рентгеновского излучения. Дело оставалось за малым — реализовать это предложение на опыте.

Для достижения поставленной цели специалистам потребовалось несколько лет на доработку ондулятора специально для этой задачи, и наконец совсем недавно результат был получен. В статье PRL 111, 034801 (2013), вышедшей в июле 2013 года, сообщается об успешном наблюдении закрученного рентгена с энергией фотонов 99 эВ. Таким образом, на шкале электромагнитных волн физика закрученного света шагнула сразу на два порядка вверх по энергии. (Более подробный рассказ об этой работе читайте в новости Закрученный свет шагнул на два порядка вверх по шкале энергий, «Элементы», 27.07.2013.)

Можно ли получить еще более высокоэнергетические закрученные фотоны, с энергиями в МэВном или даже в ГэВном диапазонах? Такие фотоны были бы шикарным инструментом исследований в ядерной физике, в физике элементарных частиц, в ускорительной физике. Здесь ситуация пока остается неясной. С одной стороны, два года назад было опубликовано заманчивое предложение использовать эффект обратного комптоновского рассеяния для получения закрученных фотонов аж ГэВных энергий. В идеале, эта схема должна работать так, как показано на рис. 5.

Рис. 5. Предложенная схема получения закрученных фотонов высокой энергии за счет процесса обратного комптоновского рассеяния. Изображение из статьи Eur. Phys. J. C71, 1571 (2011)

Предварительно закрученный оптический фотон сталкивается с электроном очень высокой энергии (например, 10 ГэВ), который сам по себе никакой закрутки не несет. Затем происходит процесс обратного комптоновского рассеяния, в результате которого существенная часть энергии электрона передается фотону. Этот процесс на обычных фотонах изучен давным-давно и уже рутинно используется в ряде научных экспериментов. Фотон рассеивается назад, под очень маленькими углами к оси столкновения, а ослабевший электрон можно затем отвести магнитным полем. Если закрученность фотона в этом процессе не изменится, мы в результате получим то, что хотели.

Проблема только в том, что закрученность точно сохраняется только при рассеянии строго назад и только при предположении, что электрон остается плосковолновым. При отклонении на небольшой угол возникают разнообразные трудности, и пока неясно, можно ли их будет преодолеть в эксперименте. Тем не менее, даже попытка поставить такой эксперимент будет очень интересной.

Закрученные электроны: создание

Несмотря на то что всё началось с фотонов, с самого начала было понятно, что закрученность может существовать и для других частиц. Главное — научиться получать аккуратные квантовые состояния таких частиц, с достаточно ровными волновыми фронтами, а уж закрутить их как-нибудь удастся. Можно даже сразу сформулировать эмпирическое правило: если от каких-то частиц удается увидеть четкую дифракционную картинку с большим количеством дифракционных полос, то такие частицы — отличный кандидат для закручивания.

Проще всего этого добиться с электронами, ведь в электронных микроскопах уже давно научились организовывать дифракцию электронов с тысячами ровненьких дифракционных полос (на эту тему есть отличная научно-популярная книжка А. Тономуры, одного из пионеров в этой области: The quantum world unveild by electron waves, к сожалению, не переведенная с английского). Так что остается лишь один вопрос: как закрутить электроны?

Опять же, чтобы избежать неправильных ассоциаций, снова подчеркнем, что слова «закрученный электрон» ни в коем случае не надо понимать, словно перед нами маленький шарик, который крутится вокруг своей оси. Напротив, электрон — это волна, волнообразное колебание электронного поля. Так же, как и в случае фотонов, закрученность — это характеристика электрона как волны, характеристика, описывающая спиралевидность его волновых фронтов. Для его визуализации сгодится та же самая картинка на рис. 2, что и для света.

В 2007 году вышла теоретическая статья PRL 99, 190404 (2007), ставшая стимулом для последовавших за ней экспериментальных работ. Авторы этой статьи внимательно изучили свойства закрученных электронов, их поведение во внешних электрических и магнитных полях и другие особенности этих состояний. В заключении статьи было перечислено несколько методов, с помощью которых закрученные электроны можно в принципе получить в эксперименте.

Рис. 6. Изображения из трех статей 2011–2012 годов, в которых были получены закрученные электроны

Спустя три года сразу несколько экспериментальных групп сумело реализовать два из этих методов.

• Хронологически первой, в апреле 2010 года, была публикация японской группы Nature 464, 737 (2010). В ней использовалась очень простая идея: друг на друга положили несколько тончайших графитовых листочков и под микроскопом нашли точку, в которой два листочка удачно накладываются один на другой так, что возникает некое подобие спиральной фазовой пластинки, но только не для света, а для электронов (рис. 6, слева). Проходя через такую импровизированную фазовую пластинку, плоская электронная волна приобретала закрученность +1 или –1, в зависимости от направления спирали.
• В сентябре того же года вышла статья бельгийско-австрийской группы Nature 467, 301 (2010), в которой описывался намного более удобный и универсальный способ получения закрученных электронов — с помощью той же дифракционной решетки с дислокацией, что использовалась для получения закрученных фотонов. Только в этом случае она должна быть намного миниатюрнее, и ее удалось получить ионным вытравливанием субмикронных бороздок нужной формы в тонкой платиновой фольге (рис. 6, в центре). Пропуская электронный луч сквозь эту решетку, исследователи расщепляли его на несколько лучей, каждый из которых нёс свою закрученность.
  Достоинствами этого метода стала чистота закрученного состояния (всё-таки, у японцев получившееся состояние было далеко от совершенства), относительная легкость воспроизведения (всё можно было реализовать внутри широко распространенного трансмиссионного электронного микроскопа) и возможность более сильного закручивания при наличии подходящих дифракционных решеток.
• Последнее свойство было блестяще продемонстрировано в статье американских физиков Science 331, 192 (2011), появившейся в январе следующего года. С помощью более сложной дифракционной решетки (рис. 6, справа) им удалось получить электроны с закрученностью вплоть до сотни!

Итак, буквально за несколько месяцев, закручивание электронов превратилось из теоретической фантазии в реально работающую методику.

Закрученные электроны: развитие и перспективы

Разумеется, получение закрученных электронов было только первым шагом в этой новой области исследования. В дальнейшем развитие пошло сразу по нескольким направлениям. Во-первых, это совершенствование технологии, то есть демонстрация новых способов получения и управления закрученными электронами, во-вторых, это их использование для экспериментальной проверки новых физических эффектов из области электродинамики и квантовой физики, и в-третьих, использование закрученных электронов как нового инструмента для сугубо прикладных задач. Перечислим только некоторые работы последних лет.

Фокусировка. Например, та же бельгийская группа в 2011 году продемонстрировала, что закрученные электроны отлично фокусируются. Их удалось сфокусировать в пятнышко размером чуть больше одного ангстрема, то есть до атомарных размеров! Это сразу открывает возможности для разнообразных практических применений, например для исследования намагниченности ферромагнитных пленок с атомарной точностью. Впрочем, здесь пока есть определенная трудность: надо понять, чем именно закрученность тут может помочь, как именно закрученные электроны позволят прощупать локальное магнитное поле, которое чувствует каждый атом.

Рис. 7. Получение закрученных электронов с помощью искусственных «магнитных монополей». Вверху: общая идея метода; внизу: электронный снимок магнитной иглы, на конце которой возникало магнитное поле, очень напоминающее монопольное. Изображение из статьи arXiv:1305.0570

«Монопольное» закручивание. Другое, совсем недавнее достижение той же группы (май 2013 года) — это реализация еще одного метода производства закрученных электронов, с помощью искусственных магнитных монополей. Настоящие магнитные монополи, конечно, пока в природе не обнаружены и неизвестно даже, разрешены ли они вообще законами физики. Но всегда можно сделать такое микроскопическое устройство, которое будет создавать магнитное поле, очень похожее на поле от магнитного монополя. Этот вариант, кстати, тоже предлагался в теоретической статье 2007 года.

Самый простой пример — это «магнитная иголка», длинный и тончайший ферромагнитный стержень, держащий сильное магнитное поле. Именно такую иглу и использовала бельгийская группа; схема эксперимента и электронная микрофотография иглы показаны на рис. 7. Вблизи одного из его кончиков, на расстояниях много больше толщины, но много меньше длины иглы, магнитное поле будет очень напоминать монопольное. Если иглу выставить поперек оси движения электронов и пропустить сквозь этот кончик электрон, то он превратится в закрученное состояние, причем степень закрутки будет пропорциональна величине магнитного поля.

Элементарные частицы. У этого способа закручивания заряженных частиц есть важное преимущество: с его помощью можно закручивать не только электроны, но и любые другие заряженные частицы, причем любых энергий. Это было бы очень удобно, например, для получения ультрарелятивистских закрученных протонов или электронов, когда никакие дифракционные решетки уже не помогут — они слишком прозрачны для частиц высокой энергии. А если такие частицы удастся создать, то, значит, их можно будет сталкивать друг с другом, и тем самым откроется новый раздел в. экспериментальной физике элементарных частиц! Ведь если у нас появляется совершенно новая характеристика начальных частиц, которой мы можем управлять, то она позволит нам изучать те особенности строения и взаимодействия элементарных частиц, которые обычным способом увидеть трудно или невозможно.

Читайте также: Секрет фокуса с появлением бутылок из цилиндра фокус

Поведение в магнитном поле. У обычного, плосковолнового электрона есть магнитный момент, возникающий из-за его спина и приблизительно равный двум магнетонам Бора. Это приводит к ряду эффектов, связанных со взаимодействием электронов с магнитным полем. Оказывается, закрученность — которая эквивалентна наличию у электрона орбитального магнитного момента — тоже влияет на его магнитный момент, она может его либо почти полностью скомпенсировать, либо усилить. Это было теоретически изучено в статье 2007 года и в последующей статье 2011 года, а затем проверено экспериментально по ларморовскому вращению (и невращению!) закрученных электронов в продольном магнитном поле, см. статью PRL 110, 093601 (2013).

Излучение от закрученных электронов. Другой пример электродинамических эффектов — излучение от закрученных электронов в различных ситуациях. В простейших вычислениях считается, что излучают движущиеся заряды — либо сами по себе, когда ускоряются, либо пролетающие внутри или вблизи среды (черенковское излучение, переходное излучение и т. п.). Но совершенно ясно, что излучать могут не только заряды, но и магнитные моменты. Теоретически такие процессы исследовались аж десятилетия назад, и потому может показаться удивительным, что такое, казалось бы, очевидное утверждение до сих пор не проверено экспериментально! Но никакой загадки тут нет: просто излучение от обычного, спинового магнитного момента исключительно слабое, и его просто не удается зарегистрировать.

Но именно здесь у закрученных электронов может быть огромное преимущество. Если добиться экстремально больших, порядка тысячи, значений величины закручивания, то пропорционально этому число возрастет и магнитный момент, а значит, резко усилятся все вызванные им процессы. В недавних теоретических статьях arXiv:1304.7363 и PRL 110, 264801 (2013) был изучен один яркий пример — переходное излучение от сильно закрученных электронов. Оказалось, что, глядя на характеристики излученных фотонов, можно напрямую убедиться, что излучение идет не только от заряда электрона, но и от его магнитного момента. Таким образом, закрученные электроны смогут экспериментально доказать реальность эффекта, который никаким другим способом заметить не получается.

Итоги

Подвести черту под этим рассказом очень просто. Закрученность — это еще одна неотъемлемая, хотя и часто забываемая, характеристика любого волнового процесса. Она сохраняется и в квантовой механике, на уровне отдельных фотонов и электронов. Закрученный свет, закрученные электроны — это вовсе не какие-то «вещи в себе», которые интересуют физиков ради них самих. Это новые инструменты для изучения физических явлений, для установления нетривиальных аналогий, для проверки законов оптики, электродинамики и квантовой механики. Это также потенциальные источники новых прикладных методов исследования и, возможно, новых технологий. Здесь многое еще остается непонятным или нереализованным, но перспективы открываются очень заманчивые. Мы надеемся, что даже небольшая подборка примеров, описанных в этом обзоре, позволила читателю в этом убедиться.

1) Да, хочется закрутить также и протоны, и нейтроны. С протонами это выглядит проще, т.к. заряженные и легче поглощаются, а значит, можно сделать аналогичные решетки с дислокацией. Как быть с нейтронами, мне пока непонятно, у них слишком большая проникающая способность. Может быть, можно взять кусок монокристалла с настоящей дислокацией и пустить волну вдоль кристаллографической оси, тогда может быть получится. Ну и второй вопрос, имеются ли источники протонов/нейтронов с хорошей поперечной когерентностью. В случае электронов это уже было нетривиальным делом, как будет для протонов, я не знаю.

2) Вас прямо-таки интересует спин-спиновое взаимодействие? Или вообще взаимодействие с чем-нибудь внешним через спин в противовес взаимодействию через заряд? Мне кажется, тут нет совсем универсального критерия. Для класса задач, который мы рассматривали, — излучение электронов за счет магнитного момента или за счет заряда, — «магнитномоментное излучение» относительно зарядового излучения подавлено маленьким множителем L*E_gamma/E_e, где L — орбитальный угловой момент, E_gamma и E_e — энергии излученного фотона и энергия налетающего электрона. Для переходного излучения и для электронов с энергией 300 кэВ, который сейчас имеются, этот параметр равен примерно L*10^ . Т.е. для L=1 всё глухо, для L=1000 уже всего лишь 1%, и этот процент можно заметить через угловую асимметрию. Если кто-нибудь когда-нибудь научится создавать закрученные электроны больше L = 10^5, то вот тогда начнется совсем новый режим, тогда излучение от магнитного момента будет сильнее зарядового. Но это пока мечты.

Спасибо за статью!
Можно в дополнение задать несколько вопросов, которые для неспециалистов могут быть интересны, для общего образования?

1. Верно ли, что скорость закрученного света меньше чем ‘c’ в вакууме?
если так, тогда, такие фотоны должны также прилетать и из космоса, причем с весьма произвольными скоростями? (или даже просто болтаться в космосе?)

2. Степень закрученности для наблюдателя, который движется навстречу или от должны отличаться?
если да, то тогда наибольшая закрученность должна наблюдаться у фотонов от далеких галактик, которые от нас быстро удаляются — поскольку если есть исходно малейшая закрученность, то она должна многократно усиллиться? (либо наоборот?)

1) Ну вот как раз задачка про скорость закрученного света была.
Там две скорости: групповая и фазовая. Групповая меньше c, фазовая больше c, их произведение равно c^2. Это для случая бесселевого закрученного света, т.е. фиксированный _продольный_ импульс и фиксированный _модуль поперечного_ импульса у каждого фотона. Для более сложных мод не знаю.

Я не думаю, что это реаьно заметить для каких-то внешних источников света. Закрученный свет надо создавать, очень тонко настраивать поперечный фронт по очень большому размеру. Если только нас не порадуют инопланетяне, мы реальных закрученных фотонов от астрофизических источников не увидим.

2) Да вроде нет, не зависит. Закрученность — это азимутальная накрутка фазы, exp(i L phi). Если вы перейдете в другую систему отсчета, которая движется вдоль оси движения, то эта азимутальная закрутка не изменится.

Я именно в эту сторону и клоню. Что будет если поместить закрученный электрон в атом? может ли он поместиться третьим на одном уровне уже имеющихся двух электронов с противоположными спинами? Или закрученность это и есть энергетические уровни в атоме?

Другими словами, можно ли получить сверхкомпактный атом упаковав все (или большинство) электроны на один энергетический уровень, раскрутив их по разному?

1. Да, конечно, можно. Плоские волны — это базис, а по базису можно разложить любое состояние. Маленькая тонкость в том, что и закрученные волны тоже образуют ортогональный базис, и значит по нему тоже можно разложить кого угодно, в том числе и плоскую волну.

2. С математической точки зрения — да, ничего не дает нового. Но весь пафос тут не в математике, а в том, что такие состояния (если хотите — такие особые комбинации плоских волн) можно реально получать и использовать, что они вполне себе устойчивы относительно малых возмущений. Вот например всякие забавные электродинамические эффекты с закрученными электронами, описанные в конце — это, с одной стороны, ничего принципиально нового, но с другой стороны, это напрямую может показать эффекты, которые другими способами не видели. С закрученным светом на днях была статья в Science про дистанционное детектирование вращения с помощью пучка закрученного света (надо бы написать про это новость) — это тоже как бы и ничего принципиально нового, но инструмент получился удобный.

3-4-5. Да я согласен, что шумиха яйца выеденного не стоит. Ну, показано, что в принципе работает, молодцы, но только у радиокоммуникации есть и гораздо более удобные приемы делать то же. Я вполне верю, что попробуй они потягаться с реально действующими схемами мультиплексирования, они бы уткнулись в эти ограничения.

2. Электроны — всё-таки существенно квантовые объекты, а я писал про классическую электродинамику.

Про дистанционное зондирование — новость видел, статью в сети не нашел, если не считать платную подписку на Science, и пока что не понял, что именно они там сделали и как посчитали? Отражали классическую ЭМ волну от вращающегося медного диска? А разве при отражении плоской ЭМ волны от движущегося в сторону плоского проводящего объекта изменяется хоть что-нибудь, кроме ортогональной компоненты волнового вектора? Или у них, действительно, какой-то макроскопический эффект, связанный именно с вращением проводящей поверхности?

Видимо, это всё же какие-то эффекты, связанные с неидеальностью проводника, от поверхности которого отражается ЭМ волна. Вообще говоря, фазовый сдвиг при отражении от поверхности неидеального проводника должен как-то зависеть от скорости его поперечного движения. Но вот наклонить луч от перпендикуляра? Хм. Угол падения равен углу отражения вроде бы и для неидеального проводника. Значит, если на вращающуюся пластину падает перпендикулярный луч, то отраженный луч тоже должен быть перпендикулярным. Как же там вообще может нарушаться осевая симметрия системы, приводящая к некой зависимости отраженного луча от угла? Или там светят под наклоном, что как-то вызывает дополнительный фазовый сдвиг?

Кстати, базис из циллиндрических волновых функций использовался в электродинамике с давних времен для расчетов поля в циллиндрических волноводах и резонаторах. Но ненулевые циллиндрические моды в остронаправленных антеннах не нашли никакого применения, видимо, потому что неизбеждый нуль как раз по оси антенны обычно не очень удобен.

А, наконец что-то прояснилось. «On page 537 of this issue, Lavery et al. (1) demonstrate that a spinning object with an optically rough surface may induce a Doppler effect in light reflected parallel to the rotation axis, provided that the light carries orbital angular momentum (OAM).» То есть, диск с оптически грубой поверхностью, облучаемый светом с фазой, непостоянной по углу поворота диска. И в диффузно рассеянном свете наблюдается эффект Допплера в виде сдвига частоты. Облучаемый вдоль оси шнек от мясорубки должен дать еще более сильный подобный эффект.

Э, нет. Вот летит электрон и у него огромный магнитный момент. Он влетает в среду и генерит переходное излучение, причем от магнитного момента его идет даже больше, чем от заряда. Это вполне себе классическая электродинамика.

Вдобавок к вашему описанию: облучается монохроматическим светом в суперпозиции +L и -L (две моды соосны). Детектируется свет под любым углом и в любой моде, хоть закрученной, хоть плосковолновой, не важно. Две моды испытывают _разный_ вращательный эффект Доплера. Разность частот между ними пропорциональна L и угловой скорости вращения объекта и не зависит ни от угла, ни от моды детектирования, ни от линейного движения объекта. В результате появляется возможность отличить вращение от просто движения (хоть вдоль луча, хоть поперечного) и измерить угловую скорость вращения. Все технические ухищрения касаются только _начального_, а не конечного луча (т.е. нужен правильный «осветитель», а детектировать может любой) — это намного удобнее, чем заставлять мерять закрученность конечного светового луча, как это предлагалось раньше (была тут даже новость: http://elementy.ru/news/164979).

Э. А давайте-ка рассмотрим экстремальный случай этой экспериментальной установки: свет от фонарика пропустим через трафарет с N щелями, чтобы получился луч с N пятнышками, расположенными по-кругу, и направим его перпендикулярно на чёрный-чёрный диск с белой кляксой. Теперь приведем диск во вращение и будем смотреть, какова интенсивность приходящего к нам рассеянного кляксой света. Осталось на результаты наблюдения навернуть наукообразия, вроде «монохроматическое излучение», «преобразование Фурье», «эффект Допплера» и, еще лучше, «две одновременные противоположно закрученные моды света», и можно посылать статейку в Science.

Это готовится свежее издание «Физики опять шутят»?

PS К сведению: устройство для измерения скорости вращения диска при помощи отраженного перпендикулярно луча света, работающее на описанном в статье принципе, только, уже «мультиплицированном», используется давным-давно и называется «оптический энкодер».

Мне кажется, вы слишком повысили градус сарказма ?

Ну да, можно вообще не париться. Смотрим в телескоп на Юпитер, следим за тем, как там пятнышки движутся по диску и определяет угловй скорость. И умных слов не надо добавлять, и так всё понятно. К чему вообще какой-то закрученный свет, солнышка вполне хватает.

Вы же не думаете, что авторы статьи совсем потеряли связь с реальностью и не понимают этих вещей? Если не думаете, то следующим логическим шагом будет поразмышлять, чем предложенный (и реализованный) ими метод лучше простого глядения в телескоп/микроскоп.

Я тут подробный список преимуществ составлять сейчас не буду, но просто скажу что ваш метод требует либо (1) узкий луч света и большую мишень, либо, если так не получается сделать, (2) хорошее оптическое разрешение при наблюдении за мишенью. Ваш метод не будет работать, когда объект маленький или находится далеко, так что попадающий на него луч на порядки шире самой мишени, и когда вы при наблюдении в микроскоп/телескоп не можете разрешить эту мишень хотя бы на пару точек. В этом случае вы получаете от объекта только общую интенсивность света и всё. Хорошо, если на мишени есть клякса и ось вращения направлена под большим углом к оси наблюдения — тогда вы хотя бы видите модуляцию яркости. Но если ось смотрит примерно на вас, вы ничего не заметите.

А этот метод не только заметит, но и измерит угловую скорость вращения.

«Вы же не думаете, что авторы статьи совсем потеряли связь с реальностью и не понимают этих вещей?»

Признаюсь, у меня возникли подобные подозрения. Есть еще другая гипотеза: авторы всё прекрасно понимают, но издеваются. ?

Схему предлагаемого эксперимента даже можно упростить: берем велосипед, ставим его вверх тормашками, светим узким лучем фонарика в области светоотражателя и, вращая колесо, наблюдаем пульсации яркости отраженного излучения с периодом, равным периоду вращения колеса. Производим преобразование Фурье интенсивности отраженного луча и обнаруживаем лес палок на сответствующих частотах, кратных частоте вращения колеса. В точности, как и авторы этой статьи, только у них за счёт осевой симметри N-го порядка луча подсветки, куча лишних палок низкого порядка отфильтрована.

Вы, действительно, не видите, почему то, что они сделали, это, по сути, то же самое? На это намекают их картинки и упоминания про то, что поверхность диска должна быть оптически неоднородной.

1. Что именно представляет собой сумма двух одинаковых по амплитуде коггерентных мод излучения с +L и -L? Будет ли в ней наблюдаться какая-либо зависимость фазы волны от угла?
2. Как будет выглядеть смещенный относительно оси колеса луч фонарика в разложении по базису из циллиндрических волновых функций с осью, совпадающей с осью колеса? Для простоты можно дальше считать, что у нас не фонарик, а монохроматическая лазерная указка.
3. Как выглядит временной спектр пульсирующего отраженного перпендикулярно обратно от отражателя на колесе луча лазерной указки? Может ли он быть монохроматическим, если у него пульсирующая огибающая? Откуда в нём взялись другие частоты, кратные частоте вращения колеса? Не из-за того ли самого «эффекта Допплера», который так старательно наблюдали авторы в этой статье?
4. Нафига там свету быть монохроматическим, если длина его волны в конечную формулу не входит?

Читайте также: Шланг рабочего цилиндра сцепления ауди 100 с4

Относительно мелких объектов — может быть, но авторы поставили эксперимент с макроскопическим диском и широким кольцом света. И там еще нужно посмотреть на реальную применимость метода для мелких объектов. Потому как ось луча должна проходить через этот малый объект, а у всех мод света с ненулевым ОАМ как раз по оси будет нуль интенсивности. Так что, эффект будет не большим, чем при освещении этого объекта просто световой волной, интенсивность которой сильно неоднородна по площади вращающегося объекта. Не спорю, возможно, такой луч сфокусировать проще на мелкий объект. Может быть. Суть эффекта от этого не меняется.

«Хорошо, если на мишени есть клякса и ось вращения направлена под большим углом к оси наблюдения — тогда вы хотя бы видите модуляцию яркости. Но если ось смотрит примерно на вас, вы ничего не заметите.»

Да неужели? Представьте, что вы подсвечиваете перпендикулярным лучем фонарика эту кляксу чуть сбоку от оси, чтобы освещенность диска была неодинакова по углу, а я смотрю с далекого расстояния вдоль оси диска в телескоп, который не может никак разрешить этот диск, но прекрасно видит пульсации яркости отраженного луча с частотой, равной частоте вращения диска. Всё там прекрасно измеряется.

PS Кстати, а разве искажения спектра при амплитудной модуляции волны когда-либо ранее называли «эффектом Доплера»? Эх, похоже, авторы статьи не просто издеваются, они в это верят.

Ладно, комментировать сарказм не буду, у каждого есть право на свое мнение. Я знаю, что у некоторых людей есть, в целом, склонность к шапкозакидательским точкам зрения, а у других людей есть, тоже в целом, склонность полутривиальное вычисление выдавать за что-то выдающееся и проталкивать во всяких там топовых журналах. Что в этой ситуации, я пока не понял, поэтому и не будут комментировать.

> . светим узким лучем фонарика в области светоотражателя .

Я же уже сказал, что речь не идет про узкие лучи. Если у вас есть узкий луч, тогда понятно, что не надо никакого закрученного света. Тут речь про то, что этот эффект будет работать и при широком луче (вы дочитайте мой пост до конца, прежде чем тыкать кнопку «ответить» ? ).

> Вы, действительно, не видите, почему то, что они сделали, это, по сути, то же самое? На это намекают их картинки и упоминания про то, что поверхность диска должна быть оптически неоднородной.

Не вижу. Разумеется, она должна быть как-то неоднородной, ведь нужно, чтоб она диффузно отражала свет, мы ж не обсуждаем зеркальное отражение. Периодичность неоднородности совершенно необязательна, она может быть беспорядочно шершавой, просто тогда свет разойдется по большому набору конечных L. Это ничего принципиально не меняет, просто интенсивность будет меньше. Но согласитесь, что вопросы про оптимизацию метода тут вторичны, ведь это proof-of-principle статья. Она просто показывает вам, что вот есть такой эффект и он вот так работает.

Кстати, а вы только картинки посмотрели или всё же прочитали статью?

Ну, вы понимаете, что это не обсуждение у доски. Поэтому я потрачу время один раз, а то комментарии и дальше будут разрастаться в геометрической прогрессии.

> 1. Что именно представляет собой сумма двух одинаковых по амплитуде коггерентных мод излучения с +L и -L? Будет ли в ней наблюдаться какая-либо зависимость фазы волны от угла?

Ну да, конечно, косинус будет при определенном выборе начала отсчета. Это вопрос на вшивость?

> 2. Как будет выглядеть смещенный относительно оси колеса луч фонарика в разложении по базису из циллиндрических волновых функций с осью, совпадающей с осью колеса?

Ну вот давайте я для бесселевых пучков напишу. Есть есть бесселево закрученное состояние |m’>_z’ относительно оси z’, то его можно разложить по базису |m>_z бесселевых же состояний относительно оси z, параллельной оси z’ и смещенной от нее в поперечном направлении на вектор \vec, характеризующийся моделем a и азимутальным углом phi_a. Разложение будет такое:

где k — модель поперечного импульса в бесселевой волне (он кстати будет одинаковым для |m’>_z’ и состояний из базиса |m>_z). Спектр мощности в этом разложени, значит, будет даваться квадратом выписанного бесселя. Т.е. чистое состояние m’ распределится в интервале порядка m’ \pm ka.

А теперь чтоб два раза не вставать, повторим то же для начального состояния (|m’>+|-m’>)_z’. Делая замену переменных (m на -m) во второй сумме, получаем (при подходящем выборе начала отсчета):

Т.е. переразложение есть, но симметричная пара раскладывается по симметричным парам.

Вопросы 3-4 по ваше колесо, но оно мне не интересно, ведь тут ситуация-то другая, тут нет необходимости в узком луче.

> Относительно мелких объектов — может быть, но авторы поставили эксперимент с макроскопическим диском и широким кольцом света.

Ну так они _показывали_ эффект, зачем им себе условия-то ухудшать. Изучение пределов применимости — это уже следующая работа. По-моему, это совершенно логично.

> Потому как ось луча должна проходить через этот малый объект, а у всех мод света с ненулевым ОАМ как раз по оси будет нуль интенсивности.

Нет конечно, не должна. Главно быть в пределах яркости луча.

> Да неужели? Представьте, что вы подсвечиваете перпендикулярным лучем фонарика эту кляксу чуть сбоку от оси, чтобы освещенность диска была неодинакова по углу, а я смотрю с далекого расстояния вдоль оси диска в телескоп, который не может никак разрешить этот диск, но прекрасно видит пульсации яркости отраженного луча с частотой, равной частоте вращения диска.

Ну да, в такой постановке работает, согласен. Ну а если освещать мы может только со своего направления, примерно совпадающего с направлением наблюдения?

Смотрите, я ж не говорю, что этот метод будет лучше всех других для _всех_ возможных постановок задачи. Я говорю, что он будет лучше всех других для _некоторых_ постановок. От него есть польза, когда общая интенсивность отраженного света от вращающегося объекта остается постоянной (имеется в виду, при обычном освещении примерно плосковолновым светом). Он позволяет в таких условиях заметить вращение (и отличить от поперечного движения) диффузно рассеивающей _неконтрастной_ поверхности.

> Кстати, а разве искажения спектра при амплитудной модуляции волны когда-либо ранее называли «эффектом Доплера»? Эх, похоже, авторы статьи не просто издеваются, они в это верят.

Ну, вы с термином «поперечный эффект Доплера» согласны? Или тоже считаете его происками неграмотных буржуев? А если две плоские волны одинаковой частоты направить под слегка разными углами на эту поверхность и увидеть, что у них частоты сдвинулись за счет поперечного эффекта Доплера, так что получается модуляция — вы это еще не отказываетесь считать эффектом Доплера? Так здесь, фактически, то же самое, только чуть более хитрая разновидность.

В общем, предлагаю на этом остановиться и заняться более насущными делами ?

Да, слишком разрослись ответы. Постараюсь написать кратко о сути. ?

1. Вопросы я задавал для обдумывания. На формулы я и не рассчитывал. ? Что я хочу показать? Вот у нас есть некий вращающийся диск с неоднородной оптической поверхностью, освещаемый неким неоднородным световым полем, пусть монохроматическим, и мы хотим рассчитать, какой именно сигнал будет на выходе детектора отраженного излучения? Не важно, луч подсветки — это специально созданные две противоположные спиральные моды, как в статье, или же просто узкий луч фонарика сбоку от оси. У нас есть минимум два равнозначных способа расчета, сложный и простой, как и в анекдоте с удалением гланд.

Во-первых, мы можем вспомнить про базис из спиральных световых волн, по которому можно разложить любую подобную световую волну, даже луч фонарика или лазерной указки. Далее, нам необходимо сказать, что каждая базисная спиральная волна не просто отражается, но и подвергается вращательному эффекту Доплера, в точности, как описано в обсуждаемой статье. Подчеркну: не важно, это авторская установка из статьи или луч фонарика. Для нахождения результата рассеяния мы должны все такие отраженные волны со сдвинутой частотой просуммировать и найти разложение поля по частоте в апертуре детектора, после чего, выполнив обратное ПФ, можно найти во временной области форму периодического с частотой вращения диска сигнала на выходе детектора. Подчеркну еще раз, это принципиально: тут нет никакой разницы, это пара мод как в статье или же узкий луч фонарика сбоку от центра, раскладываемый по спиральным модам в очень длинный ряд.

Но есть и другой, более традиционный способ расчета сигнала на выходе нашего детектора отраженного света. Пользуясь принципом Гюйгенса-Френеля мы можем легко посчитать приходящую в детектор волну, отраженную неподвижным диском, повернутым на угол фи и освещаемым нашим неравномерным, но стационарным световым полем. Далее, учитывая огромное отношение частоты вращения диска и частоты света, мы просто разворачиваем фи линейно по времени и непосредственно получаем форму сигнала на выходе детектора. Опять же: совершенно не важно, освещает диск пара противоположных мод, как в статье, или же узкий луч фонарика сбоку от центра диска. Результат получится точно такой же, как и по первому методу через спирали и Доплеров.

Вот только такая двойственность задачи подсказывает, что, как минимум, приоритет авторов в наблюдении вращательного эффекта Доплера явно надуман, так как его наблюдал с детства каждый, кто видел пульсирующий свет, отраженный отражателем на колесе едущего велосипеда в свете автомобильных фар или просто оптически неоднородной поверхностью вращающейся тарелки. Если такую задачу расписать по базису из спиральных гармонических волн, необходимо придется ввести в рассмотрение и некий эффект Доплера для объяснения сдвигов частот волн, приводящих просто к нестационарности наблюдаемой рассеянной вращающимся предметом картины. Но традиционно такие не совсем стационарные задачи всё же считаются горадо проще в квазистатике без необходимости разложения по базису спиральных волн, а размазывание спектра объясняется просто модуляцией отраженного луча, вызванной интерференцией неоднородностей освещающего луча _и_ оптических неоднородностей на поверхности диска.

2. Не хочу спорить о терминологии. Нравится называть это всё наблюдением эффекта Доплера — пожалуйста. В конце концов, в науке тоже важны красивые названия для популярности идей. Вот только не будет никакой разницы между результатом наблюдения детектором рассеянного света от картинки, наклеенной на вращающийся диск, или же анимированным мультиком на экране подходящего ЖК индикатора, изображающего эту вращающуюся картинку. С точностью до дискрета обновления картинки на индикаторе и иных погрешностей рисования на нём картинки, разумеется.

3. Относительно использования для малых объектов. Да, можно поместить малый объект сбоку от центра завернутого луча, где интенсивность излучения ненулевая. Но тогда нам всё равно придется преобразовать задачу к базису из спиральных волн, проходящих через центр вращения малого объекта, чтобы для них учесть вращательные эффекты Доплера по алгоритму, подробно описанному мною в п. 1. В этом базисе наши красивые две противоположные спиральные моды превратятся в длинный ряд разложения по самым разным спиральным модам, и, боюсь, традиционный анализ в квазистатике и без Доплеров окажется сильно проще, как это было для луча фонарика. Если, конечно, речь не идет про существенно квантовый объект, с которым, в любом случае, всё нетривиально.

4. У двух противоположно закрученных спральных мод с осью, совпадающей с осью вращения диска, есть всё же одно преимущество по сравнению с фонариком: полное отсутствие нулевой угловой гармоники, бесполезной для детектрирования вращения, но попадающей в детектор.

5. Относительно того, какие нужны неоднородности на диске. Понятно, что чтобы посчитать рассеяние шершавостями на поверхности диска некоторой спиральной моды, нужно разложить комплексный коэффициент отражения самих шершавостей по круговым функциям. Если соответствующий коффициент в разложении вдруг равен нулю, то никакого отражения соответствующей спиральной моды вместе со всеми обсуждаемыми эффектами Доплера от таких шершавостей просто не будет. Так что, несимметрия отражающей способности поверхности диска для этих эффектов всё же принципиальна.

PS А, перечитав статью, заметил вот такой маленький абзац в статье: «Within the time domain, the interpretation is that the superposition of two helically phased beams with opposite values of ‘ creates a beam cross section with a modulated intensity of 2‘ radial petals (18). Therefore, the light scattered from the rough surface of a spinning disc will undergo an intensity modulation also given by Eq. 4.»

И еще заметил рассуждения про вектор Пойнтинга, который наклонён у спирального света, что они связывают с ненулевым ОАМ. Но у суммы двух противоположных мод он вообще-то прямее всех прямых. Полный ОАМ у их измертельного луча света вообще-то равен нулю. Как, кстати, и у отдельных фотонов в этом луче. Так что вообще мы тут обсуждаем?

Уважаемый автор, день добрый!
Вопрос возник по абз.№2 Главы «Закрученный свет: краткая история: -«Фотон, излученный возбужденным атомом, распространяется в виде расширяющейся волны сразу во все стороны. Когда такой фотон попадает в какое-то регистрирующее устройство или вызывает какой-то иной физический процесс, то он воздействует локально, лишь маленьким кусочком своего фронта — и тут же происходит квантовый коллапс световой волны, и от его «закрученности» не остается и следа».

Извиняюсь, а как это фронт волны распространяется во все стороны, ведь согласно закону сохранения импульса у него имеется конкретный вектор скорости (отдача приходится на излученный атом). И еще один очень фантастический эффект наблюдается, что фронт волны уходит в виде сферы на достаточно большое расстояние от источника (атома) и потом локально производится взаимодействие, тогда «коллапс волнового фронта» может происходить со сверхсветовой скоростью, поскольку диаметральные части сферического фронта могут быть на очень большом расстоянии, а процесс коллапса должен быть фактически мгновенный же. Или я что-то всё ни так понял.

🌟 Видео

Жидкий пластик из оргстекла, легко! Эксперименты и применение своими руками!Скачать

Акриловая смола и оргстеклоСкачать

Для начинающих инвертер с модифицированным синусомСкачать

Чем акрил отличается от оргстекла?Скачать

Простая самоделка для гибки пластика и оргстекла, сделать может каждыйСкачать

Термоструна или гибочный станок для акрила и т.п.Скачать