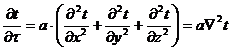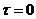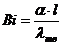Аналитическое решение уравнения теплопроводности в цилиндре (6 видео)

Видео:Уравнение теплопроводности в цилиндрических координатахСкачать

Постановка задачи и вывод дифференциального уравнения теплопроводности для сплошного цилиндра. Аналитическое решение.

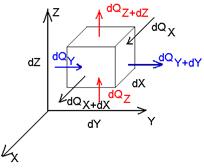
Дифференциальное уравнение теплопроводности выводится на основе закона сохранения энергии. Из всего рассматриваемого объема выделим элементарный объем dV и процесс будем рассматривать в течении элементарного промежутка времени.

· Тепло физические параметры среды постоянны

· Температурной деформацией пренебрегаем

· Внутренний источник тепла , если он есть, распределен по всему объему

dQ₁ – количество тепла подведенного к рассматриваемому объему dV за время dτ за счет процессов электропроводности

dQ₂ – количество тепловой энергии, которой выделяется на dV за dτ за счет действия внутреннего источника тепла

dQ – изменение внутренней энергии рассматриваемого объема за dτ (изменение энтальпии тела).

Ø Методы переноса тепла: теплопроводность, тепловая конвекция, излучение

Ø Конвективный обмен – возможен только в подвижных средах. Перенос осуществляется только за счет перемещение самого вещества.

Ø Тепловое излучение – перенос тепла происходит в 2 этапа. Сначала тепло преобразуется в тепловую энергию, а затем обратно.

Ø Теплопроводность – перенос тепла в твердых телах, жидкостях или газах, если жидкость и газы неподвижны.

Механизм данного явления объясняется на основании молекулярно — кинетических изменений. Перенос энергии осуществляется вследствие теплового движения и энергетического взаимодействия между микрочастицами (молекулами, атомами, электронами), из которых состоит данное тело.

Теплопроводность в чистом виде существует только в твердых телах. А в подвижных средах теплообмен осуществляется за счет теплопроводности, конвекции и излучения.

По теплопроводности тепло распространяется от нагретых участков к холодным, то есть в сторону убывания температуры.

Температура определяет степень нагретости тела.

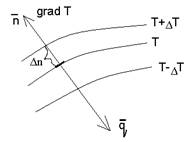
Процесс теплопроводности неразрывно связан с распределением температуры внутри тела, поэтому необходимо дать определение температурному полю и градиенту температуры:

— температурным полем называется совокупность значений температуры в каждой точке пространства в данный момент времени

Геометрическое место точек в пространстве имеющих одинаковую температуру, называется изотермической поверхностью

Поскольку любая точка пространства в данный момент времени может иметь только одно значение температуры, то изотермические поверхности не пересекаются →

— температурный градиент – предел отношения изменения температуры ΔТ к расстоянию между изотермами по нормали Δn.

Lim (ΔТ / Δn) _Δ_n→0 = = grad T. -единичный вектор

Является вектором, направленным по нормали к изотермической поверхности в сторону возрастания температуры его размерность [ 0 С/м]

Наибольшее изменение температуры может происходить по нормали к изотермическим поверхностям.

· Количества тепла, прошедшего через произвольную изотермическую поверхность за некоторый интервал времени τ – будем обозначать P [Вт]

· Количества тепла, прошедшего через произвольный изотермическую поверхность в единицу времени будем обозначать – тепловой поток Q [Дж].

· Тепловой поток отнесенный к единице поверхности, называется плотностью теплового потока – q [Вт/м 2 ]

· Закон Фурье (связь q и grad T). Фурье экспериментально установил что, количество переданного тепла пропорционально падению температуры, времени и площади сечения, перпендикулярного направлению распространению тепла

· λ – коэффициент теплопроводности – представляет собой количество тепла, которое роходит в единицу времени через один квадратный метр изотремической поверхности при температурном градиенте =1

В общем случаи λ зависит от температуры

Читайте также: Крепление для цилиндра сцепления ваз

· С – теплоемкость – количество энергии необходимого для нагрева 1 кг вещества на 1 градус. [Дж/кг 0 С]

dQ_X = q_X * dY * dZ * dτ

dQ₂ = q_V dV dτ, где q_V – количества тепла выделившегося в единице объема в единицу времени (внутренний источник тепла).

dQ = dU = ρ C dV dτ , где ρ – плотность среды [кг/м 3 ]

Из закона Фурье:

а – коэффициент температура проводность [м 2 / 0 С]

Постановка задачи:

1. рассматриваем сплошной цилиндр

3. цилиндрическая система координат

4. теплофизические свойства постоянны

5. внутреннего источника тепла нет (q_V =0)

Переходим от декартовой системы координат к цилиндрической:

Цилиндрические (Ц) и декартовые (Д) координаты связаны следующим образом:
Д ® Ц	Ц ® Д

Оператор Лапласа для цилиндрической системы координат запишется:

С учетом поставленной задачи получаем:

Охлаждение (нагревание) бесконечного длинного цилиндра.

Цилиндр радиусом г₀ отдает теплоту окружающей среде через свою боковую поверхность; коэффициент теплоотдачи α во всех точках поверхности одинаков и остается постоянным на протяжении всего периода охлаждения. Температура среды Tcp постоянна. В начальный момент времени при τ = 0 температура является некоторой функцией T (r, 0) = f (r). При этих условиях уравнение теплопроводности принимает вид:

Граничные и начальные условия:

· при τ = 0 и 0 0 и r = 0

· при τ > 0 и r = r₀

Сформулированную задачу решим с помощью разделения переменных, т. е.

(r, τ) = φ (τ) ψ (r).

Подставив это выражение в уравнение (*),получим два обыкновенных дифференциальных уравнения вида

Если обозначить kr₀ = μ , тогда частное решение уравнения (*) будет иметь вид:

где — коэффициент температуро-проводность

Постоянная μ определяется из граничных условий (r= r₀), решение которых приводит к характеристическому уравнению:

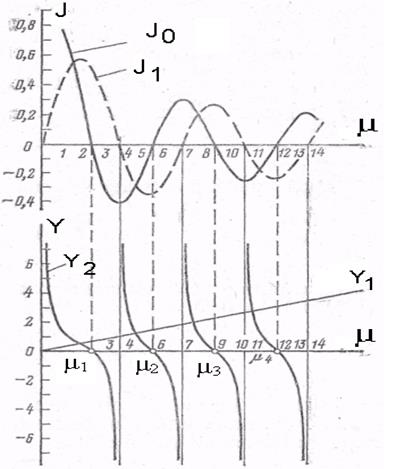
(2) где J₁, (μ) — функция Бесселя первого рода первого порядка.

Уравнение (+) является трансцендентным, и его удобно решать графическим способом, обозначив:

· Отметим, что у₂ обращается в нуль в тех точках, для которых Jo (μ) = 0.

· В тех точках, в которых функция J₁ (μ₁) обращается в нуль, функция у₂ претерпевает разрыв непрерывности и становится равной ± оо.

Функции Jo (μ) и J₁ (μ) являются периодическими затухающими функциями.

— Кривая у₂ = напоминает котангенсоиду, но с убывающим периодом.

— Функция у₁ графически представляет прямую линию, проходящую через начало координат.

Выполнив построение, как показано на рис, в точках пересечения функции у₂ с прямой у₁ получим значения корней характеристического уравнения

Из рис следует, что уравнение (2) имеет бесчисленное множество решений, а сами корни, представляют ряд возрастающих чисел, т. е. μ₁ 100) прямая совпадает с осью абсцисс и корни характеристического уравнения не зависят от Bi, а определяются из условий

· Если рассматривать охлаждение цилиндра при условии Bi → 0

· Если Fo ≥ 0,25, при вычислении безразмерной температуры можно ограничиться первым членом ряда. Допускаемая при этом ошибка не превысит 1 %.

Дата добавления: 2016-04-19 ; просмотров: 2672 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Горицкий А. Ю. - Уравнения математической физики. Часть 2 - Уравнение теплопроводностиСкачать

Решение задач нестационарной теплопроводности.

НЕСТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ.

Общие положения. Описание процесса.

Ранее были рассмотрены условия распространения теплоты при стационарном режиме, когда температурное поле не менялось во времени, оставалось постоянным.

Читайте также: Как проверить неработающий цилиндр

Если же температурное поле меняется во времени, т.е. является функцией времени, то протекающие в таких условия процессы называются нестационарными.

Нестационарные процессы теплопроводности встречаются при охлаждении и нагреве металлических заготовок, прокалывании твердых тел, в производстве стекла, обжига кирпича и т.д.

В качестве примера рассмотрим такой случай. Тело внесено в среду более высокой температурой; сразу же между средой и телом возникает процесс теплообмена, и тело начинает прогреваться. Сначала нагреваются поверхностные слои, но постепенно процесс прогрева распространяется вглубь тела (рис. 1.6.1).

По истечении некоторого времени (теоретически бесконечно большого) температура всех частей тела выравнивается и становится равной температуре окружающей среды, т.е. наступает тепловое равновесие.

На рис. 1.6.1 показан характер кривых, полученных при нагревании однородного твердого тела в среде с постоянной температурой .По мере нагрева температура в каждой точке асимптотически приближается к температуре нагревающей среды. Наиболее быстро изменяется температура точек, лежащих вблизи поверхности тела. С увеличением времени прогрева эта разность будет уменьшаться и теоретически через достаточно большой отрезок времени она будет равна нулю.

При нестационарном режиме количество переданной теплоты также непостоянно во времени (рис. 1.6.2). По мере прогрева тела количество воспринимаемой теплоты уменьшается и в пределе становится равным нулю. Площадь, заключенная между осями и кривой, определяет собой полное количество теплоты, переданное за время . Эта теплота аккумулируется телом. Нестационарные тепловые процессы всегда связаны с изменением внутренней энергии или энтальпии вещества.

Аналогичным образом протекает и процесс охлаждения тела, при этом выделенная теплота передается в окружающую среду.

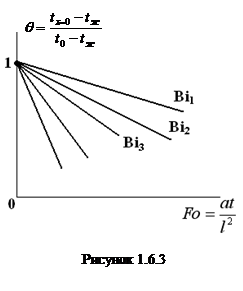
Скорость теплового процесса при нестационарном режиме определяется значением коэффициента температуропроводности

а , .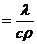

Любой процесс нагревания или охлаждения тела можно разделить на три режима.

Первый режим — начало процесса.

Характерной особенностью этого режима является распространение температурных возмущений в пространстве и захват все новых и новых слоев тела. Скорость изменения температуры в отдельных точках при этом режиме различна и зависит от начальных условий.

Это режим неупорядоченного процесса.

С течением времени скорость изменения температуры во всех точках тела становится постоянной. Это режим упорядоченного процесса, он называется регулярным режимом.

По прошествии длительного времени наступает третий режим, характерной особенностью которого является постоянство распределения температур во времени – это стационарный режим.

Например, в работе паровых котлов нестационарный режим возникает лишь при пуске в работу, выключении и изменении режима работы и имеет временный характер. Поэтому расчет таких аппаратов производится лишь для основного, стационарного режима, а для нестационарного совсем не рассчитывается. В работе же нагревательных печей, наоборот, нестационарный режим является основным, при их расчете приходится определять время, необходимое для прогрева металла до заданной температуры, или температуру, до которой металл нагреется в течение определенного промежутка времени.

Описанный характер изменения температуры и количества переданной теплоты справедливы лишь для твердых тел.

Решение задач нестационарной теплопроводности.

Решить задачу нестационарной теплопроводности это значит найти зависимость изменения температуры и количество теплоты переданной телу во времени для любой точки тела:

Для аналитического нахождения этих зависимостей может быть использовано дифференциальное уравнение теплопроводности Фурье:

Читайте также: Тормозная попала в цилиндр

Это уравнение решается с помощью рядов Фурье. Аналитическое решение получается очень сложным и возможно лишь для тел простой формы (пластины, цилиндра и шара) при целом ряде упрощающих предпосылок.

Аналитическое описание процесса теплопроводности кроме дифференциального уравнения также включает в себя и условия однозначности.

Условия однозначности задаются в виде:

· физических параметров , , ;

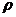
· формы и геометрических размеров объекта ;

· температуры тела в начальный момент времени ; t = t₀ = f(x, у, z).

· граничных условий, которые могут быть заданы в виде граничных условий третьего рода:

Дифференциальное уравнение теплопроводности совместно с условиями однозначности дает законченную математическую формулировку рассматриваемой задачи. Решение ее заключается в отыскании функции, которая удовлетворяла бы уравнению и условиям однозначности.

t=f(x,y,z,i,a,t₀,t_ж, )

Если решить это уравнение для плоской стенки и рассмотреть процесс изменения температуры только в одном направлении x, то решение будет иметь следующий вид:

где b иcопределяются из условий стационарности процесса, т.е. при ;

, — из граничных условий 3 рода;

— из начальных условий, т.е. при .

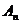
Из уравнения видно, что искомая функция t зависит от большого числа переменных, которые можно сгруппировать в 3 безразмерных комплекса, эти комплексы называются числами подобия.

Первое число подобия — Число Био:

где — коэффициент теплоотдачи на границе жидкости и твердого тела;

λ — коэффициент теплопроводности твердого тела;

l— характеристический размер, который определяется в зависимости от формы тела:

для цилиндра l= ;

для шара l= .

Второе число подобия — Число Фурье:

гдеa— коэффициент температуропроводности;

Число Фурье называют также безразмерным временем.

Третий безразмерный комплекс — безразмерная координата:

Установлено, что θ— безразмерная температура, является функцией чисел Био и Фурье, для фиксированных значений , т.е.

Изменение безразмерной температуры θ для центра ( 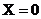) и поверхности ( ) можно представить графическим решением, которое приведено на рисунке 1.6.3.

Аналитическое решение уравнения теплопроводности в цилиндре

Подобные графики построены для центра и поверхности пластины, цилиндра и шара, а так же для безразмерного количества теплоты, которая является функцией числа Bi и :

Следовательно, чтобы определить температуру на поверхности или в центре тела необходимо знать две величины: число Bi и число .

Таким образом, метод решения задач нестационарной теплопроводности заключается в следующем:

1) задаются геометрическими, начальными и граничными условиями [(с;λ; ; ;α; ),( или )];

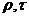
2) вычисляют числа Bi и ;

, ;

3) зная числа Bi и по графику, определяют безразмерную температуру θ;

4) определив θ, рассчитывают температуру в центре

где — начальная температура тела;

— температура среды.

Рассмотрим влияние значений чисел Bi на распределение температуры в теле на примере охлаждения пластины.

Из полученного решения следует, что для любого момента времени температурное поле имеет вид симметричной кривой с максимумом на оси пластины ( ). В каждый последующий момент будет своя кривая, монотонно убывающая к поверхности (рис. 1.6.4).