Видео:9 класс, 41 урок, ЦилиндрСкачать
1. AC=8 , ∠CAB=60*
Найти: Sбок
2. ∠AO1B=60*, AB=15,OA=9
Найти: Sбок
Видео:Объём цилиндраСкачать
Ответы 2
1)Sбок. цил.= 2×pi×r×h, r=AB/2, h=CB, pi=
3,14(иногда pi оставляют в ответе )
sin60°=CB/8, (корень из 3)/2=CB/8, CB= (8корней из 3)/2=4×корней из 3
Sбок. цил.=2*3,14×2×4 корней из 3=50,24 корней из 3 (или = 16корней из 3 ×pi)
2)Sбок. цил.= 2×pi×r×h, r=OA=OB, h=OO1, pi=
3,14(иногда pi оставляют в ответе )
треугольник AOB-египетский, тк у него стороны равны соотношению 3:4:5
(ну или решать через теорему Пифагора OB²=15²-9², OB=Корень из 144,OB=12)
в цилиндр можно вписать только равнобедренный треугольник
=>доп.построение:продолжим сторону OB до пересечения с окружностью, пусть эта сторона BB1=12×2=24=B1O1=O1B
OO1²=24²-12², OO1=12 корней из 3
Sбок. цил.=2×pi×12×12корней из3=288корней из 3×pi
я согласен с этим высказыванием. существуют слова, которые автору создать неповторимый образ, картину. писателю воздействовать на читателя, вызывают в читателе особые чувства, отношения к изображаемому. такими словами являются эпитеты. эпитеты- это красочные определения, выраженные прилагательными в полной форме. умело подобранным эпитетам, картина становится необыкновенной. в доказательство примеры из текста:
в качестве примера возьмём предложение №5. вэтом предложении автор употребляет эпитет «шкодливому внуку», выраженный прилагательным в полной форме для того, чтобы дать образную характеристику мальчика. показать нам какой он был шаловливый, склонный к проказам, озорной. также возьмём предложение №46. в это предлжении автор употребляет эпитет «счастливый мальчик», выраженный прилагательным в полной форме для того, чтобы передать нам то счастье, которое испытывал мальчик в тот момент. так, за нескаолько лет он впервые испытал это чувство, так как враги за пару минутпревратились в настоящих друзей.
Читайте также: Задиры в цилиндрах восстановление
таким образом, могу сделать вывод, что эпитеты автору сказать о чувствах человека, а также дать образную характеристику.
Видео:60. Площадь поверхности цилиндраСкачать
Цилиндр. Решение задач — Цилиндр — ЦИЛИНДР, КОНУС И ШАР
— формировать навыки решения задач на нахождение элементов цилиндра, площади поверхности цилиндра;
— закрепить знания, умения учащихся по изучаемой теме;
— развивать самостоятельность учащихся в работе над задачами. Используемый дополнительный материал: задачи на готовых чертежах.
Объявление темы и цели урока.
II. Актуализация знаний учащихся
1. Укажите среди окружающих вас предметов объекты, имеющие цилиндрическую форму.
2. Дайте определение цилиндра и его основных элементов.
3. Что такое осевое сечение цилиндра? Каков его вид?
4. Может ли осевое сечение быть: а) прямоугольником; б) квадратом; в) трапецией? Почему?
5. Цилиндр катится по плоскости. Какая фигура получается при движении его оси?
Проверка домашнего задания (три ученика работали у доски во время устной работы класса).
3. 
4.
5.
(Ответ: )
Решение: Осевые сечения равны, значит, при наложении они совпадут. Но высоты цилиндров не равны: а ≠ b. (Ответ: нет.)
1.
2. 
3.
4.
Решение задач по готовым чертежам.
I уровень — устно с обсуждением решения: № 1, 2, 3.
II уровень — самостоятельное решение с самопроверкой по готовым ответам: № 4, 5, 6.
2. ΔADC — прямоугольный. Так как AD = 4, то АС = 5 (пифагорова тройка).
2. Так как ∠BAC = 30°, то ВС = 1/2АВ, т. е. ВС = 2.
3.
4.
Дано: О1А = 5, AA1 = 15, АВ = 17.
Найти: расстояние между OO1 и АВ.
1. ΔАА1В — прямоугольный; по теореме Пифагора 
ДП: ОК, К — середина ВА1.
2. ОK ⊥ A1B (так как ОК — расстояние между ОО1 и АВ:
Читайте также: Главный тормозной цилиндр зил 4331
3. По теореме Пифагора из ΔA1KO: 
1. АО = 5 — дополнительное построение.
2.
4.
Дано:
1.
2.
Дано: ABCD — осевое сечение.
Найти:
1. Sбок. = 2πRH, ABCD — прямоугольник.
2.
3.
2. Так как O1К — расстояние от точки О до ABCD, то О1К ⊥ ABCD, О1К ⊥ ВС.
3. АВ = ВС = 12 см ⇒ ВК = 6 см.
5. ΔВКО1 — прямоугольный, по теореме Пифагора.
2. 
3. ΔОКА1 — прямоугольный, ∠К = 90°. ОA1 =R.
4.
5. 
(Ответ: )
3.
4.
— На этом уроке мы отрабатывали навыки решения задач на нахождение элементов цилиндра и совершенствовали полученные знания при решении задач.
П. 53, 54. I уровень — № 527, 531. II уровень — № 531, 544, 601.
Решение задач из домашнего задания.
1. Достроим плоскость, содержащую АВ так, чтобы А1ВВ1А || OO1.
3. O1К ⊥ A1B, О1К — расстояние от OO1 до АА1ВВ1, так как O1К ⊥ АА1ВВ1, К — середина А1В.
4. r = 10 дм, d = O1K = 8 дм, AB = 13 дм.
5. 
6. (так как ΔAA1В — прямоугольный).
2. O1К- расстояние от ОО1 до ABCD. O1К = 9 дм, К-середина ВС.
4. 240 = 10 · ВС, ВС = 24 дм, ВК = 12 дм.
5. ΔВКО1 — прямоугольный, (Ответ: 15 дм.)
2.
3.
4.
(Ответ: )
1) ABCD — осевое сечение; OA = R, P- середина ОА; MLKN ⊥ ОА;
2) ABCD и MLKN — прямоугольники;
3)
5) ΔМРО — прямоугольный 
6)
7)
8)
(Ответ: )
Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.
Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.
Читайте также: Как проверить главный тормозной цилиндр ваз 21099
Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.
Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.
© 2014-2021 Все права на дизайн сайта принадлежат С.Є.А.
🎬 Видео
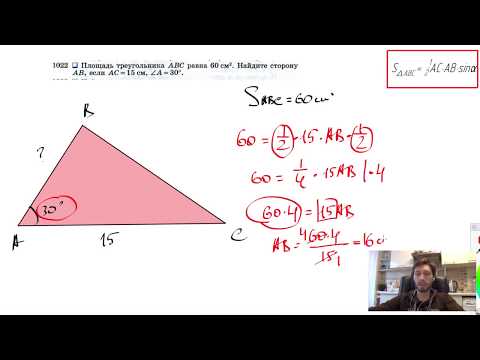
№1022. Площадь треугольника ABC равна 60 см2. Найдите сторону АВ, если АС= 15 см,Скачать
РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать
#130. Задание 8: комбинация телСкачать
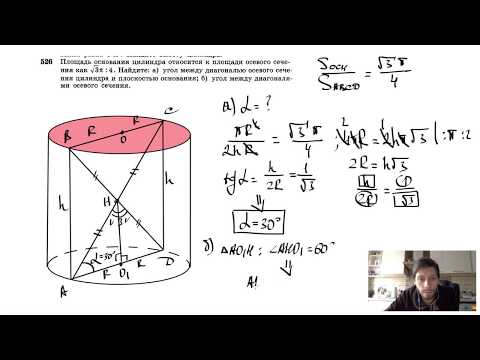
№526. Площадь основания цилиндра относится к площади осевого сечения как √3π:4. Найдите:Скачать
№529. Высота цилиндра равна 8 см, радиус равен 5 см. Найдите площадь сечения цилиндраСкачать
Задача про ЦИЛИНДР / Как найти объем детали? / Профиль ЕГЭСкачать
№523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высотуСкачать
2017 на окружности по разные стороны от диаметра AB взяты Точки M и NСкачать
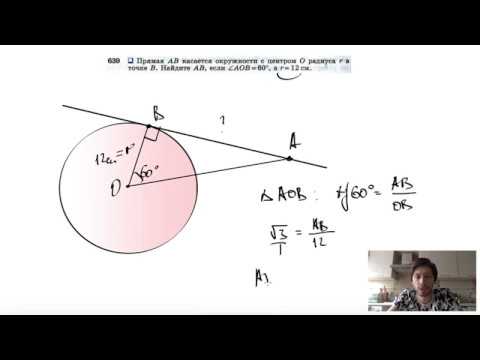
№638. Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВСкачать
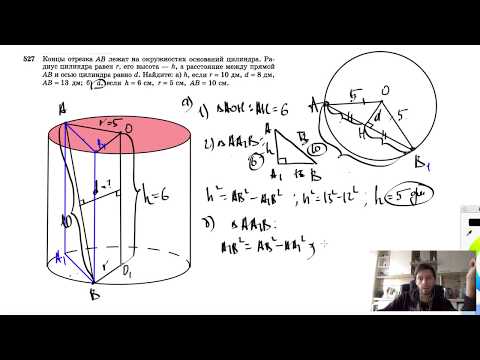
№527. Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус цилиндра равен г,Скачать
59. Понятие цилиндраСкачать
№639. Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВСкачать
№521. Докажите, что осевое сечение цилиндра является прямоугольником, две противоположныеСкачать
ЗАДАНИЕ 8 из ЕГЭ_53Скачать
№538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевогоСкачать
№652. На полуокружности АВ взяты точки С и D так, что ∪AC=37°, ∪BD=23°. Найдите хорду CD,Скачать
№1025. С помощью теорем синусов и косинусов решите треугольник ABC, если:Скачать
