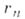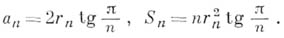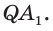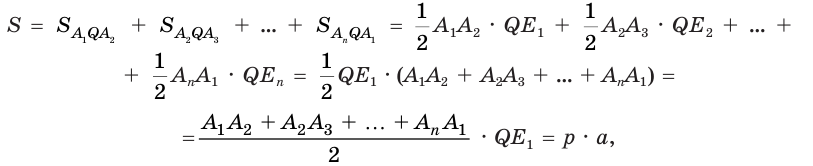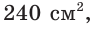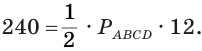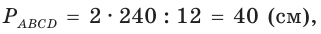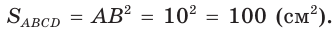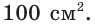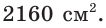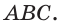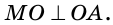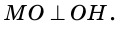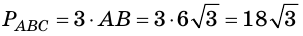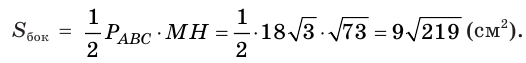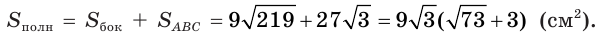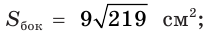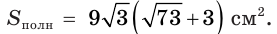1. геометр. перпендикуляр, опущенный из центра правильного многоугольника на любую из его сторон, а также длина этого перпендикуляра ◆ Апофема правильного многоугольника равна радиусу вписанной в него окружности.
- Делаем Карту слов лучше вместе
- Предложения со словом «апофема»
- Отправить комментарий
- Дополнительно
- Предложения со словом «апофема»
- Морфология
- Правописание
- Карта слов и выражений русского языка
- апофема
- Смотреть что такое «апофема» в других словарях:
- АПОФЕМА
- Смотреть что такое «АПОФЕМА» в других словарях:
- Пространственные фигуры — виды, изображения, свойства с примерами решения
- Пространственные фигуры
- Изображение пространственных фигур
- 💥 Видео
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова пореформенный (прилагательное):
Предложения со словом «апофема»
Отправить комментарий
Дополнительно
Предложения со словом «апофема»
Да к тому же, непонятно почему, у меня в голове вертелось слово апофема.
Морфология
Правописание
Карта слов и выражений русского языка
Онлайн-тезаурус с возможностью поиска ассоциаций, синонимов, контекстных связей и примеров предложений к словам и выражениям русского языка.
Справочная информация по склонению имён существительных и прилагательных, спряжению глаголов, а также морфемному строению слов.
Сайт оснащён мощной системой поиска с поддержкой русской морфологии.
Видео:АпофемаСкачать

апофема
Энциклопедический словарь . 2009 .
Смотреть что такое «апофема» в других словарях:
АПОФЕМА — См. АПОТЕМА. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. АПОФЕМА см. АПОТЕМА. Словарь иностранных слов, вошедших в состав русского языка. Павленков Ф., 1907 … Словарь иностранных слов русского языка
АПОФЕМА — (от греч. apotithemi откладываю) ..1) отрезок (а также его длина) перпендикуляра а, опущенного из центра правильного многоугольника на любую из его сторон2)] В правильной пирамиде апофема высота боковой грани … Большой Энциклопедический словарь
апофема — сущ., кол во синонимов: 3 • апотема (2) • длина (10) • перпендикуляр (4) Словарь … Словарь синонимов
АПОФЕМА — (1) длина перпендикуляра, опущенного из центра окружности, описанной вокруг правильного многоугольника, на любую из его сторон; (2) высота боковой грани правильной пирамиды; (3) высота трапеции, являющейся боковой гранью правильной усечённой… … Большая политехническая энциклопедия
Апофема — (от греч. apotithçмi откладываю в сторону) 1) длина перпендикуляра, опущенного из центра правильного многоугольника на любую из его сторон (рис. 1); 2) в правильной пирамиде А. высота а ее боковой грани (рис 2). Рис. 1 к… … Большая советская энциклопедия
АПОФЕМА — (от греч. apotfthemi откладываю) 1) отрезок (а также его длина) перпендикуляра а, опущенного из центра правильного многоугольника на любую из его сторон. 2) В правильной пирамиде А. высота а боковой грани (см. рис.). К ст. Апофема … Большой энциклопедический политехнический словарь
Апофема — длина перпендикуляра, опущенного из центра правильного многоугольника на одну из его сторон; апофема равна радиусу вписанного в данный многоугольник круга. А. также называли наклонную сторону конуса … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
АПОФЕМА — (от греч. apotithemi откладываю), 1) отрезок (а также его длина) перпендикуляра а, опущенного из центра правильного многоугольника на любую из его сторон. 2) В правильной пирамиде А. высота а боковой грани … Естествознание. Энциклопедический словарь
апофема — апофема, апофемы, апофемы, апофем, апофеме, апофемам, апофему, апофемы, апофемой, апофемою, апофемами, апофеме, апофемах (Источник: «Полная акцентуированная парадигма по А. А. Зализняку») … Формы слов
АПОФЕМА — правильного многоугольника отрезок (а также его длина) перпендикуляра, опущенного из центра правильного многоугольника на любую из его сторон. А. правильного n угольника равна радиусу вписанной в него окружности и связана сего стороной an и… … Математическая энциклопедия
Видео:ОБЪЕМ ЦИЛИНДРА #shorts #егэ #огэ #математика #профильныйегэСкачать

АПОФЕМА
правильного многоугольника — отрезок (а также его длина) перпендикуляра, опущенного из центра правильного многоугольника на любую из его сторон. А. правильного n-угольника равна радиусу вписанной в него окружности и связана сего стороной a n и площадью S n соотношениями
А. правильной пирамиды — высота ее боковой грани.
Читайте также: Протяжка блока цилиндров ваз 2110
Математическая энциклопедия. — М.: Советская энциклопедия . И. М. Виноградов . 1977—1985 .
Смотреть что такое «АПОФЕМА» в других словарях:
АПОФЕМА — См. АПОТЕМА. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. АПОФЕМА см. АПОТЕМА. Словарь иностранных слов, вошедших в состав русского языка. Павленков Ф., 1907 … Словарь иностранных слов русского языка
АПОФЕМА — (от греч. apotithemi откладываю) ..1) отрезок (а также его длина) перпендикуляра а, опущенного из центра правильного многоугольника на любую из его сторон2)] В правильной пирамиде апофема высота боковой грани … Большой Энциклопедический словарь
апофема — сущ., кол во синонимов: 3 • апотема (2) • длина (10) • перпендикуляр (4) Словарь … Словарь синонимов
АПОФЕМА — (1) длина перпендикуляра, опущенного из центра окружности, описанной вокруг правильного многоугольника, на любую из его сторон; (2) высота боковой грани правильной пирамиды; (3) высота трапеции, являющейся боковой гранью правильной усечённой… … Большая политехническая энциклопедия
Апофема — (от греч. apotithçмi откладываю в сторону) 1) длина перпендикуляра, опущенного из центра правильного многоугольника на любую из его сторон (рис. 1); 2) в правильной пирамиде А. высота а ее боковой грани (рис 2). Рис. 1 к… … Большая советская энциклопедия
апофема — (от греч. apotíthēmi откладываю), 1) отрезок (а также его длина) перпендикуляра а, опущенного из центра правильного многоугольника на любую из его сторон. 2) В правильной пирамиде апофема высота а боковой грани. * * * АПОФЕМА АПОФЕМА (греч.… … Энциклопедический словарь
АПОФЕМА — (от греч. apotfthemi откладываю) 1) отрезок (а также его длина) перпендикуляра а, опущенного из центра правильного многоугольника на любую из его сторон. 2) В правильной пирамиде А. высота а боковой грани (см. рис.). К ст. Апофема … Большой энциклопедический политехнический словарь
Апофема — длина перпендикуляра, опущенного из центра правильного многоугольника на одну из его сторон; апофема равна радиусу вписанного в данный многоугольник круга. А. также называли наклонную сторону конуса … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
АПОФЕМА — (от греч. apotithemi откладываю), 1) отрезок (а также его длина) перпендикуляра а, опущенного из центра правильного многоугольника на любую из его сторон. 2) В правильной пирамиде А. высота а боковой грани … Естествознание. Энциклопедический словарь
апофема — апофема, апофемы, апофемы, апофем, апофеме, апофемам, апофему, апофемы, апофемой, апофемою, апофемами, апофеме, апофемах (Источник: «Полная акцентуированная парадигма по А. А. Зализняку») … Формы слов
Видео:Объём цилиндраСкачать

Пространственные фигуры — виды, изображения, свойства с примерами решения
Пространственные фигуры:
Геометрические фигуры делятся на плоские и пространственные в зависимости от того, все или не все точки фигуры принадлежат одной плоскости.
Видео:Апофема правильной пирамиды. Задание А2 из ЦТ 2020 #цт2020Скачать

Пространственные фигуры
Некоторые пространственные фигуры — призма (рис. 1), пирамида (рис. 2), цилиндр (рис. 3), конус (рис. 4), шар (рис. 5). Раздел геометрии, в котором изучаются плоские фигуры, называется планиметрией, а раздел, в котором изучаются пространственные фигуры, — стереометрией.
Ту или иную пространственную фигуру приходится изображать на плоскости листа в тетради или на плоскости доски. Соответствующий рисунок выполняют таким образом, чтобы он создавал то же впечатление, что и сама изображаемая фигура. При этом невидимые линии делают штриховыми.
На рисунке 6 изображены параллелограмм 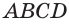
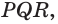
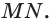
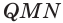
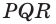
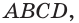
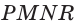
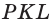
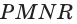
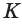
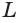
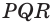
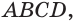
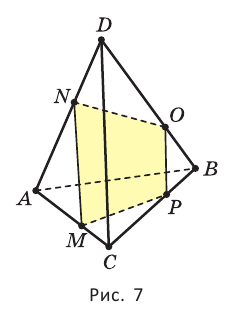
На рисунке 7 изображена треугольная пирамида 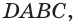
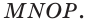
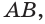
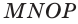
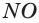
Представление пространственной фигуры на рисунке называют изображением фигуры.
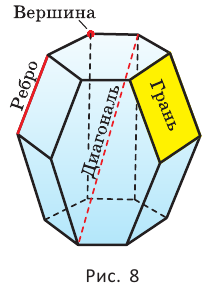
Важным классом пространственных фигур являются многогранники, под которыми понимают тела, ограниченные плоскими многоугольниками.
Эти многоугольники называются гранями многогранника, их вершины — вершинами многогранника, а стороны — рёбрами многогранника.
Отрезок, соединяющий две вершины многогранника, не принадлежащие одной грани, называется диагональю многогранника (рис. 8).
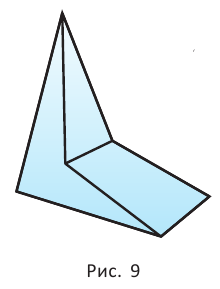
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой своей грани. На рисунке 9 изображён невыпуклый многогранник.
Б) Мы будем изучать простейшие выпуклые многогранники — призмы и пирамиды.
Призмой называется многогранник, две грани которого — равные 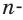
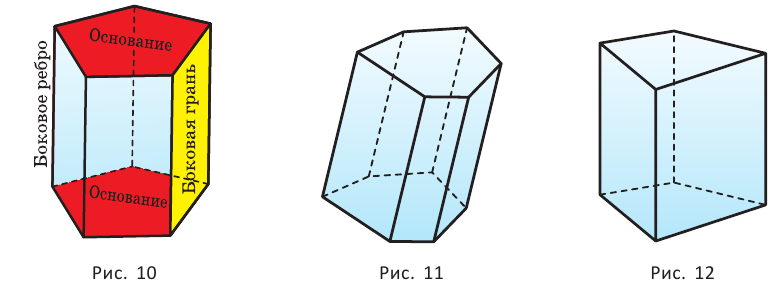
Равные грани-многоугольники призмы называют её основаниями, а остальные грани — боковыми гранями. Рёбра боковых граней, не принадлежащие основаниям, называются боковыми рёбрами (рис. 10).
В зависимости от количества сторон основания призмы отличают треугольную, четырёхугольную, пятиугольную и т. д. призмы. На рисунке 11 изображена шестиугольная призма.
Читайте также: Замена главного тормозного цилиндра honda accord 8
Совокупность боковых граней призмы образуют боковую поверхность.
Площадь боковой поверхности призмы равна сумме площадей боковых граней.
Призмы разделяются на прямые и наклонные.
Прямая призма — призма, боковые грани которой являются прямоугольниками. Обычно, изображая прямую призму, её боковые рёбра проводят вертикально (рис. 12).
Призма прямая, если боковые рёбра перпендикулярны рёбрам основания призмы.
Призма наклонная, если боковые рёбра не перпендикулярны рёбрам основания призмы.
Прямая призма называется правильной, если её основания являются правильными многоугольниками.
Призма, основаниями которой являются параллелограммы, называется параллелепипедом.
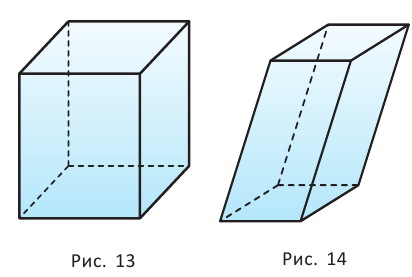
Параллелепипед, как и призма, может быть и прямым (рис. 13), и наклонным (рис. 14).
Прямой параллелепипед, основания которого являются прямоугольниками, называется прямоугольным параллелепипедом.
Все грани прямоугольного параллелепипеда являются прямоугольниками.
Три ребра прямоугольного параллелепипеда, сходящиеся в одной вершине, называются измерениями прямоугольного параллелепипеда.
Прямоугольный параллелепипед с равными измерениями называется кубом.
Все грани куба — равные друг другу квадраты.
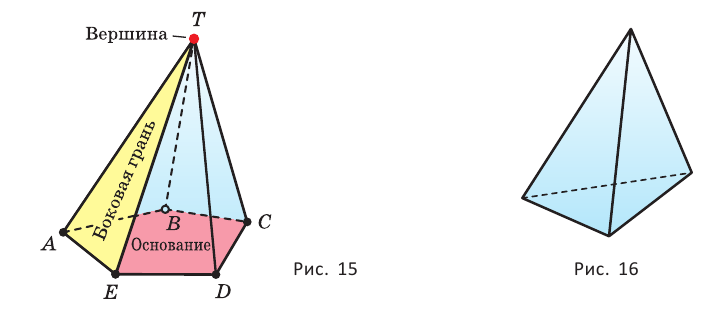
В) Пирамидой называется многогранник, одна грань которого — многоугольник, а остальные являются треугольниками с общей вершиной.
На рисунке 15 изображена пирамида 
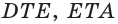
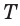
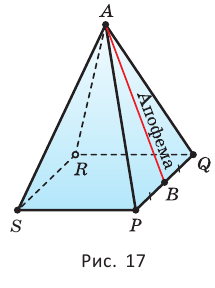
В зависимости от количества сторон основания пирамиды отличают треугольную, четырёхугольную, пятиугольную и т. д. пирамиды. Пирамида на рисунке 15 — пятиугольная, а на рисунке 16 — треугольная.
Пирамида, основание которой — правильный многоугольник, а отрезок, соединяющий её вершину с центром основания, перпендикулярен любой прямой, проведённой в плоскости основания через этот центр, называется правильной.
Высота боковой грани правильной пирамиды, опущенная из вершины пирамиды, называется апофемой пирамиды.
На рисунке 17 изображена правильная четырёхугольная пирамида 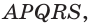
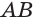
Теорема 1. У правильной пирамиды равны её: а) боковые грани; б) апофемы.
Доказательство: Пусть 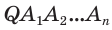
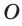
а) Поскольку треугольники 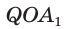
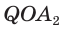
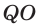
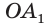
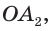
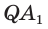
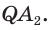
Боковые грани пирамиды — равнобедренные треугольники с равными боковыми сторонами. Основания этих треугольников также равны друг другу как стороны правильного многоугольника, который лежит в основании пирамиды. Поэтому боковые грани равны между собой по трём сторонам.
б) Поскольку боковые грани пирамиды 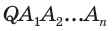
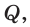
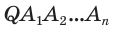
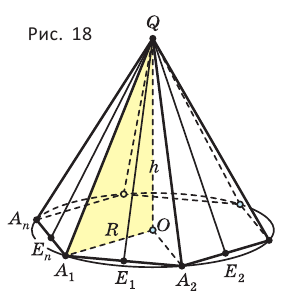
Теорема 2. Площадь боковой поверхности правильной пирамиды равна произведению полупериметра её основания и апофемы.
Доказательство: Пусть 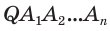
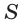
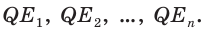
где 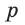
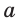
Г) Ещё один класс пространственных фигур составляют тела вращения, к которым относятся цилиндр, конус, шар.
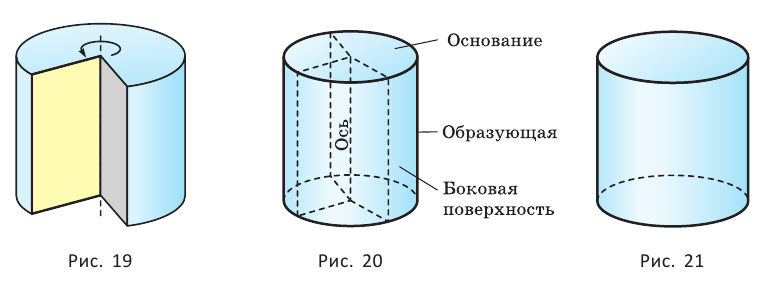
Цилиндром называется тело, полученное вращением прямоугольника вокруг одной из его сторон (рис. 19). При этом вращении одна сторона прямоугольника остаётся неподвижной, её называют осью цилиндра. Сторона, противолежащая оси, образует поверхность, которую называют боковой поверхностью цилиндра, а саму сторону — образующей цилиндра. Ещё две стороны прямоугольника при вращении образуют поверхности, которые являются равными кругами, эти круги называют основаниями цилиндра (рис. 20). На рисунке 21 дано изображение цилиндра.
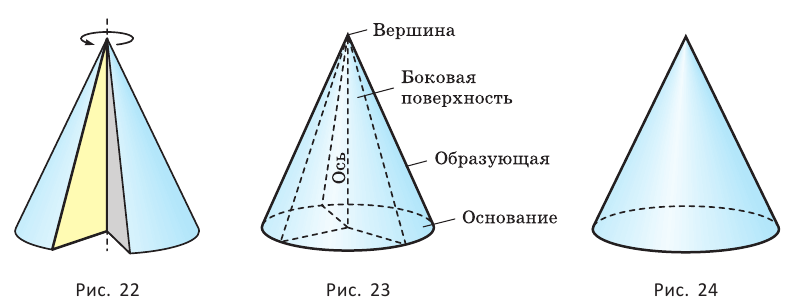
Конусом называется тело, полученное вращением прямоугольного треугольника вокруг одного из его катетов (рис. 22), который называют осью конуса. Второй катет описывает круг, который называют основанием конуса; неподвижную вершину треугольника, которая не принадлежит основанию, называют вершиной конуса. Гипотенуза при вращении образует поверхность, которую называют боковой поверхностью конуса, саму гипотенузу называют образующей конуса (рис. 23). На рисунке 24 дано изображение конуса.
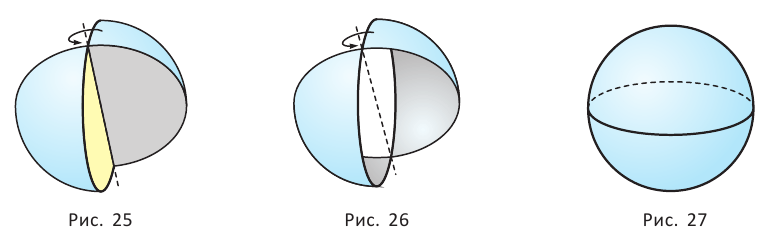
Шаром называется тело, полученное вращением круга вокруг своего диаметра (рис. 25). При этом вращении окружность описывает поверхность, которую называют сферой (рис. 26). На рисунке 27 дано изображение шара.
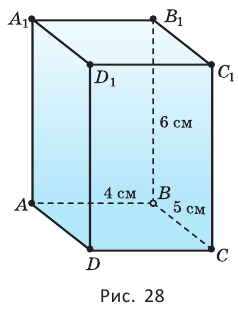
Найдите площадь боковой поверхности прямой четырёхугольной призмы, в основании которой лежит прямоугольник с измерениями 4 см и 5 см, а боковое ребро равно 6 см.
Пусть 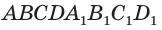
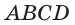
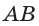
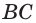
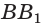
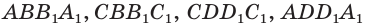
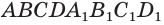
Ответ:
Боковая поверхность прямой призмы равна произведению периметра её основания и бокового ребра. Докажите это самостоятельно.
Читайте также: Как снять тормозной цилиндр с заднего колеса ваз 2114
Боковая поверхность правильной четырёхугольной пирамиды равна а её апофема — 12 см. Найдите площадь основания пирамиды.
Пусть 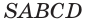
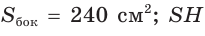
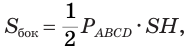
Тогда 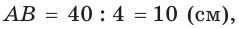
Ответ:
Площадь боковой поверхности пирамиды равна сумме площадей её боковых граней.
Апофема правильной четырёхугольной пирамиды равна 30 см, а отрезок, соединяющий вершину пирамиды с центром основания, — 24 см. Найдите боковую поверхность пирамиды.
Пусть 
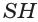
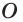
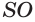
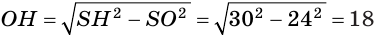
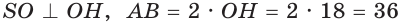
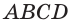
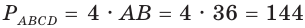
(см2),
так как пирамида правильная.
Ответ:
В правильной пирамиде отрезок, соединяющий центр основания пирамиды с основанием апофемы пирамиды, — радиус окружности, вписанной в основание пирамиды. Докажите это самостоятельно.
Сторона основания 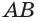
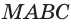
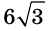
б) боковую поверхность пирамиды;
в) полную поверхность пирамиды.
Пусть 
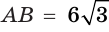
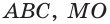
a) 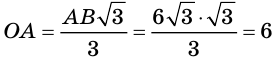
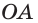
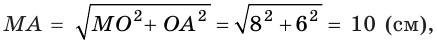
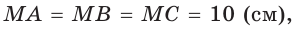
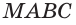
б) Пусть 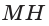
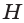
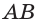
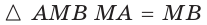
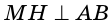
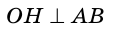
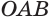
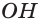
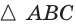
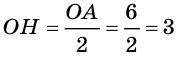
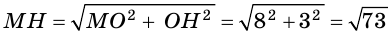
(см),
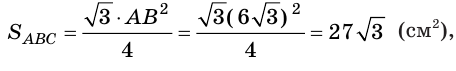
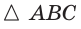
В)
Ответ: а) 
в)
Площадь полной поверхности пирамиды равна сумме площади боковой поверхности и площади основания
Изображение пространственных фигур
Чтобы получить изображение призмы, достаточно построить многоугольник — основание призмы. Из вершин основания провести прямые, параллельные некоторой фиксированной прямой, и отложить на них одинаковые отрезки. Соединив концы этих отрезков, получим многоугольник — изображение другого основания призмы.
Чтобы получить изображение пирамиды, достаточно построить изображение основания пирамиды, выбрать некоторую точку в качестве изображения вершины пирамиды и соединить её с вершинами многоугольника основания пирамиды.
Не каждый рисунок воспринимается нами как изображение реально существующей фигуры. Расхожее выражение «обман зрения» по сути является неверным. Глаза не могут обмануть нас, поскольку являются лишь промежуточным звеном между объектом и мозгом человека. Обман обычно возникает не из-за того, что мы видим, а из-за того, что неосознанно рассуждаем и непроизвольно ошибаемся.
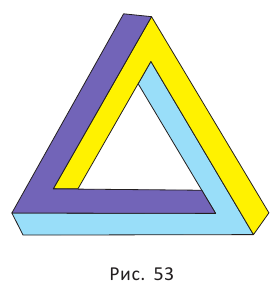
Невозможные объекты представляют собой рисунки на двумерной плоскости, изображающие трёхмерные структуры, существование которых в реальном трёхмерном мире представляется невозможным. Классическим примером такой простой фигуры является невозможный треугольник Пенроуза (рис. 53). В этом треугольнике каждый угол сам по себе является возможным, но парадокс возникает тогда, когда мы рассматриваем его целиком. Стороны треугольника направлены одновременно и на зрителя, и от него, поэтому отдельные части треугольника не могут образовать реальный трёхмерный объект.
Наш мозг интерпретирует рисунок на плоскости как трёхмерную модель. Сознание задаёт «глубину», на которой находится каждая точка рисунка. Наши представления о реальном мире сталкиваются с противоречием, с определённой непоследовательностью, и приходится делать некоторые допущения: прямые двумерные линии интерпретируются как прямые трёхмерные линии; двумерные параллельные линии интерпретируются как трёхмерные параллельные линии; острые и тупые углы интерпретируются как прямые углы в перспективе; внешние линии рассматриваются как граница формы, которая крайне важна для восприятия определённого изображения.
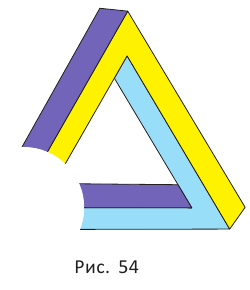
Человеческое сознание сначала создаёт общий рисунок предмета, а затем анализирует его отдельные части. Каждый угол совместим с пространственной перспективой, но, соединившись, они образуют пространственный парадокс. Если закрыть любой из углов треугольника (рис. 54), то невозможность существования исчезает.
Похожие фигуры явились источником вдохновения для многих творцов. График Маурицио Эшер создал ряд литографий (рис. 55), которые принесли ему известность художника-иллюзиониста.
- Геометрия
- Аналитическая геометрия
- Начертательная геометрия
- Взаимное расположения прямых на плоскости
- Треугольник
- Решение треугольников
- Треугольники и окружность
- Объем фигур вращения
- Длина дуги кривой
- Геометрические фигуры и их свойства
- Основные фигуры геометрии и их расположение в пространстве
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
💥 Видео
Видеоурок по математике "Цилиндр"Скачать

ПЛОЩАДЬ боковой поверхности ЦИЛИНДРАСкачать

Случайно или специально врезался в CLS 🤦🏻♂️?Наберите тут 100 к лайков ,если ждете продолжение 🔥Скачать

10 класс, 33 урок, Правильная пирамидаСкачать

Цилиндр. Определение, свойства, формулы.Скачать

ВСЕ О ПИРАМИДАХ! ЧАСТЬ I #shorts #егэ #огэ #математика #геометрия #пирамидаСкачать

Объем цилиндраСкачать

11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Цилиндр | Геометрия 7-9 класс #124 | ИнфоурокСкачать

9 класс, 41 урок, ЦилиндрСкачать

11 класс. Геометрия. Объем цилиндраСкачать

как замерить выработку поршня и цилиндраСкачать

Как найти площадь боковой поверхности цилиндра #shorts #математика #геометрия #репетитор #огэ #егэСкачать

Академия Shamir. УТОЧНЕНИЕ ЦИЛИНДРАСкачать

11 класс. Контрольная №4 (из 6). Тема: Объем призмы, цилиндра и конуса. Решение с советами! :)Скачать

ГЕОМЕТРИЯ 11 класс: Цилиндр. Площадь поверхностиСкачать