Бесконечная нить заряжена с плотностью цилиндр заряженный с плотностью (7 видео)

Бесконечная нить заряжена с плотностью цилиндр заряженный с плотностью

Продемонстрируем возможности теоремы Остроградского-Гаусса на нескольких примерах.

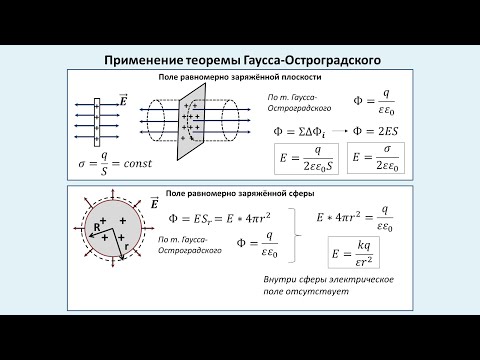
Поле бесконечной однородно заряженной плоскости

Поверхностная плотность заряда на произвольной плоскости площадью S определяется по формуле:

где d q – заряд, сосредоточенный на площади d S; d S – физически бесконечно малый участок поверхности.

Пусть σ во всех точках плоскости S одинакова. Заряд q – положительный. Напряженность во всех точках будет иметь направление, перпендикулярное плоскости S (рис. 2.11).

Видео:Электростатика | электрическое поле бесконечной нити (тонкого цилиндра)Скачать

Очевидно, что в симметричных, относительно плоскости точках, напряженность будетодинакова по величине и противоположна по направлению.

Представим себе цилиндр с образующими, перпендикулярными плоскости, и основаниями ΔS, расположенными симметрично относительно плоскости (рис. 2.12).


Рис. 2.11	Рис. 2.12

Применим теорему Остроградского-Гаусса. Поток Ф_Е через боковую часть поверхности цилиндра равен нулю, т.к . Дляоснования цилиндра

Суммарный поток через замкнутую поверхность (цилиндр) будет равен:

Внутри поверхности заключен заряд . Следовательно, из теоремы Остроградского–Гаусса получим:

откуда видно, что напряженность поля плоскости S равна:

Полученный результат не зависит от длины цилиндра. Это значит, что на любом расстоянии от плоскости

Поле двух равномерно заряженных плоскостей

Пусть две бесконечные плоскости заряжены разноименными зарядами с одинаковой по величине плотностью σ (рис. 2.13).

Видео:Применение теоремы Гаусса-Остроградского. Напряжённость поля пластины, сферы и шара.Скачать

Результирующее поле, как было сказано выше, находится как суперпозиция полей, создаваемых каждой из плоскостей .

Вне плоскостей напряженность поля

Полученный результат справедлив и для плоскостей конечных размеров, если расстояние между плоскостями гораздо меньше линейных размеров плоскостей (плоский конденсатор).

Между пластинами конденсатора действует сила взаимного притяжения (на единицу площади пластин):

Механические силы, действующие между заряженными телами, называют пондермоторными.

Тогда сила притяжения между пластинами конденсатора:

где S – площадь обкладок конденсатора. Т.к. , то

Видео:Урок 224. Напряженность поля неточечных зарядовСкачать

Читайте также: Найдите объем цилиндра если осевое сечение является квадратом

Это формула для расчета пондермоторной силы.

Поле заряженного бесконечно длинного цилиндра (нити)

Пусть поле создается бесконечной цилиндрической поверхностью радиуса R, заряженной с постоянной линейной плотностью , где d q – заряд, сосредоточенный на отрезке цилиндра (рис. 2.14).

Из соображения симметрии следует, что Е в любой точке будет направлена вдоль радиуса, перпендикулярно оси цилиндра.

Представим вокруг цилиндра (нити) коаксиальную замкнутую поверхность (цилиндр в цилиндре) радиуса r и длиной l (основания цилиндров перпендикулярно оси). Для оснований цилиндров для боковой поверхности т.е. зависит от расстояния r.

Следовательно, поток вектора через рассматриваемую поверхность, равен

Видео:Бесконечная заряженная плоскость [Физзадачи #1]Скачать

При на поверхности будет заряд По теореме Остроградского-Гаусса , отсюда

Если , т.к. внутри замкнутой поверхности зарядов нет (рис.2.15).

Если уменьшать радиус цилиндра R (при ), то можно вблизи поверхности получить поле с очень большой напряженностью и, при , получить нить.

Поле двух коаксиальных цилиндров с одинаковой линейной плотностью λ, но разным знаком

Внутри меньшего и вне большего цилиндров поле будет отсутствовать (рис. 2.16) .

В зазоре между цилиндрами, поле определяется так же, как и в предыдущем случае:

Видео:Теорема Гаусса для расчета полей цилиндра (нити) и плоскостиСкачать

Это справедливо и для бесконечно длинного цилиндра, и для цилиндров конечной длины, если зазор между цилиндрами намного меньше длины цилиндров (цилиндрический конденсатор).

Поле заряженного пустотелого шара

Пустотелый шар (или сфера) радиуса R заряжен положительным зарядом с поверхностной плотностью σ. Поле в данном случае будет центрально симметричным, – в любой точке проходит через центр шара. ,и силовые линии перпендикулярны поверхности в любой точке. Вообразим вокруг шара – сферу радиуса r (рис. 2.17).

Если то внутрь воображаемой сферы попадет весь заряд q, распределенный по сфере, тогда

Внутри сферы, при поле будет равно нулю, т.к. там нет зарядов:

Читайте также: Течь из переднего тормозного цилиндра