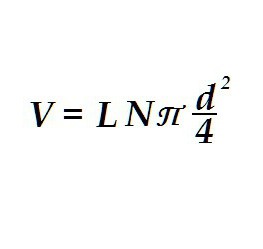Бесконечный цилиндр это цилиндр у которого диаметр

Видео:СЛУГА БЕСКОНЕЧНОГО ЦИЛИНДРА Eternal Cylinder PartnerСкачать

Что такое цилиндр: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Видео:СЕКРЕТНЫЙ Путь За Цилиндр - The Eternal CylinderСкачать

Определение цилиндра

Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.

Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.

Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O₁O₂ на 180° или прямоугольников ABO₂O₁/O₁O₂CD вокруг стороны O₁O₂ на 360°.

Видео:КОЛОБКИ ДОСТАЛИ 3 ЛИНЗЫ The Eternal CylinderСкачать

Основные элементы цилиндра

• Основания цилиндра – два одинаковых по размеру/площади круга с центрами в точках O₁ и O₂.
• R – радиус оснований цилиндра, отрезки AD и BC – диаметры (d).
• O₁O₂ – ось симметрии цилиндра, одновременно является его высотой (h).
• l (AB, CD) – образующие цилиндра и одновременно с этим стороны прямоугольника ABCD. Равны высоте фигуры.

Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.

• длина данного прямоугольника равна длине окружности основания цилиндра ( 2πR );
• ширина равна высоте/образующей цилиндра.

Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.

Видео:МУТИРУЙ И БЕГИ! ► The Eternal Cylinder |1| ПрохождениеСкачать

Большая Энциклопедия Нефти и Газа

Видео:СЮЖЕТ БЕЗ ЦИЛИНДРА #15 The Eternal Cylinder ПрохождениеСкачать

Бесконечный цилиндр

Ток / однородно распределен по сечению бесконечного цилиндра радиуса R . Используя максвелловский тензор натяжений, найти силу F, прижимающую друг к другу две одинаковые половины цилиндра. Здесь F — сила, приложенная к единице длины одной из половин цилиндра. [31]

Таким образом, напряженность поля вне равномерно заряженного бесконечного цилиндра определяется выражением (82.5), внутри же его поле отсутствует. [32]

Перемешанная масса выходит из глиномесилки в виде бесконечного цилиндра . Ее режут на куски, из которых формуют тигли и крышки. [33]

О двух задачах кручения усиленного тонким покрытием бесконечного цилиндра в условиях неоднородной ползучести / / Докл. [34]

ДВУХМЕРНОЕ ТЕЛО — тело, имеющее форму бесконечного цилиндра , образующая которого дает в поперечном сечении фигуру двухмерного тела. [35]

На рис. 1 приведено поле температур в бесконечном цилиндре . [36]

С некоторыми оговорками это же справедливо и для бесконечного цилиндра . Бесконечный плазменный цилиндр со спадающей к кожуху плотностью, р О, очевидным образом неустойчив относительно винтовых возмущений, поскольку в малой окрестности магнитной оси для каждой магнитной поверхности существует неустойчивое резонансное возмущение Сайдема. [37]

Будем моделировать сетчатый электрод двумя взаимно перпендикулярными системами параллельных бесконечных цилиндров радиусом Кц, расположенных на расстоянии а друг от друга и лежащих в одной плоскости. В таком случае электрическое поле можно определить как суперпозицию полей, создаваемых каждым цилиндром, а поле скоростей определить из задачи об обтекании бесконечного цилиндра при условии, что остальные цилиндры не искажают течение. Подобное предположение будет нарушаться в окрестности узлов сетки и возле края электрода. Однако если размер электрода много больше периода сетки а, а период сетки велик по сравнению с Кц, то в большей части электрода это предположение справедливо. [38]

Структура армированных пластиков рассматривается как система определенным образом расположенных бесконечных цилиндров , представляющих собой армирующий наполнитель, пространство между которыми заполнено однородной полимерной матрицей. В такой модели структура материала может быть количественно описана объемной долей полимера или наполнителя и геометрическими параметрами пространственной решетки наполнителя. Все основные теоретические закономерности получены на подобных моделях. Однако, как уже указывалось, реальные пластики представляют собой не полностью упорядоченную стохастическую систему, которую сложно количественно описать с помощью небольшого числа параметров. [40]

Читайте также: Как определить площадь полной поверхности цилиндра

Таким образом, внутри равномерно заряженного по поверхности круглого бесконечного цилиндра поля нет. [41]

Решить задачу 418 о дифракции плоской волны на бесконечном цилиндре , не предполагая цилиндр идеально проводящим, но считая его поверхностный импеданс С малым. [42]

Найти электростатическое поле равномерно заряженного ( р const) бесконечного цилиндра . [43]

В этом случае быстро кристаллизующийся компонент образует супернематическую систему практически бесконечных цилиндров диаметром менее 1 мкм, устойчивых, пока сохраняется матрица В, и часто ( хотя и не всегда) рассыпающихся в пыль при отжиге заведомо ниже температуры плавления чистого компонента А. [44]

Эта оценка была получена путем экстраполяции соответствующих результатов для бесконечных цилиндров малого радиуса при т, меняющемся от 2 до 8, и п — сю. [45]

Видео:ЭВОЛЮЦИЯ В МИРЕ ЦИЛИНДРА ( The Eternal Cylinder )Скачать

Жизнь в космосе: Цилиндр О’Нила

Многие люди верят, что Земля вскоре окажется в опасности, и что размашистая природа человечества послужит тому причиной. Благодаря быстрому техническому прогрессу последних нескольких веков мы стремительно истощаем ресурсы Земли, чтобы обеспечить наши промышленные потребности и глобальную торговлю. Футуристы склонны считать, что у нас не останется иного выбора, кроме как исследовать и колонизировать космическое пространство, когда доступные ресурсы на Земле, наконец, подойдут к исчерпанию.

Тем не менее, создание космической среды обитания является нелегкой задачей и сопряжено с серьезными проблемами, такими как строительство объектов в космосе, воссоздание пригодных для жизни условий, рециркуляция и переработка отходов, моделирование искусственной гравитации и т.д. Но промышленный эффект и главный приз в случае реализации этих замыслов — возможность извлекать энергию Солнца в невиданных масштабах за счет размещения гигантских солнечных панелей на обслуживаемых корпусах в космосе.

Одна из наиболее тщательно продуманных концепций будущих космических обиталищ — Цилиндр О’Нила. Это внушительных размеров конструкция, состоящая из двух вращающихся цилиндров, предложенная известным физиком Джерардом О’Нилом несколько десятилетий назад.

Происхождение идеи цилиндра

Преподавая физику своим студентам в Принстонском университете, О’Нил поручил им разработать концепцию орбитальной мегаструктуры, чтобы продемонстрировать, что жизнь и выживание в космосе действительно возможны. Его ученики придумали множество проектов для размещения человека во враждебной среде космоса. После долгого сеанса мозгового штурма О’Нил свел их теории к идее цилиндрической конструкции космического поселения. Позже, дополнительные детали и функционал этой структуры были опубликованы в Physics Today в 1974 году; предложенный концепт был назван цилиндром О’Нила.

Конструкция цилиндра О’Нила

Конструкция состоит из двух цилиндров, вращающихся на подшипнике в противоположных направлениях, чтобы смягчить гироскопический эффект. Предполагалось, что каждый цилиндр будет иметь длину 20 миль и диаметр 5 миль, с 6 широкими продольными полосами (3 обитаемых пространства и 3 окна). О’Нил предполагал, что промышленные процессы и объекты для отдыха будут расположены на центральной оси — практически в условиях невесомости.

Гравитационное моделирование

Одним из ключевых различий между жизнью на Земле и жизнью в космосе (или на любом другом астрономическом теле) является разница в гравитации. Искусственная гравитация необходима для воссоздания условий, в которых нуждается человеческий организм, приспособленный к силе тяжести на Земле, и у цилиндра О’Нила есть все возможности для достижения именно этого. Поскольку два гигантских цилиндра вращаются вокруг своей оси, они будут использовать центростремительную силу любого объекта на внутренней поверхности для создания искусственной гравитации. Учитывая размеры конструкции и подставляя величину ускорения свободного падения (9,81) в уравнение: a = v² / r , мы можем сделать вывод, что цилиндру потребуется совершать полный круг вращения примерно 28 раз в час, чтобы моделировать гравитационную силу Земли.

Воссоздание земной среды

Поддержание атмосферы подобной земной является следующей проблемой при возведении космической колонии. Цилиндр О’Нила разумно спроектирован, чтобы поддерживать соотношение газов аналогичное тому, что встречается на Земле. Тем не менее, есть одна оговорка : давление внутри цилиндра будет вдвое меньше земного, что, впрочем, не окажет существенного влияния на наше дыхание. Напротив, этот незначительный компромисс даст ряд преимуществ, поскольку снизится общая потребность в газе, и отпадет нужда строить слишком толстые стены, чтобы сдерживать давление. В предлагаемом цилиндре О’Нила также предусмотрены механизмы, за счет которых среда обитания сможет контролировать свой собственный микроклимат, используя расположение зеркал и изменяя соотношение газов в цилиндре.

Читайте также: Задний тормозной цилиндр газ 53 размер

Симуляция дня и ночи

Когда среда обитания человека находится в космическом вакууме, цилиндр превращается в огромный термос! Теоретический концепт О’Нила пытался преодолеть эту проблему, используя систему зеркал, прикрепленных к каждому из трех окон. Таким образом, прямой солнечный свет может быть направлен в цилиндр для имитации дневного времени. Точно так же, повернув зеркало в сторону, можно воссоздать и ночные сумерки. Эта искусственная «ночь» будет выполнять и другую важную функцию — позволять излишкам накопленного за «день» тепла покидать цилиндр.

Несмотря на технически обоснованную конструкцию цилиндра О’Нила, идея слишком сложна, чтобы ее можно было воплотить в жизнь с помощью наших сегодняшних технологий. До настоящего времени его реализация была ограничена областью научной фантастики. Однако, учитывая усилия таких организаций как SpaceX и Mars One , возможно, когда-нибудь цилиндры О’Нила действительно помогут человечеству освоиться на бескрайних просторах космоса!

А далее речь пойдет об идеальных местах в космосе для размещения островов О’Нила.

Ставьте палец вверх , если вам понравился материал, делитесь им в соц. сетях и подписывайтесь на канал. До новых встреч!

Видео:КОНЕЦ БЕСКОНЕЧНОГО ЦИЛИНДРА И МАТЕМАТИКА The Eternal CylinderСкачать

Цилиндр. Виды, объём цилиндра, площадь поверхности

Название науки «геометрия» переводится как «измерение земли». Зародилась стараниями самых первых древних землеустроителей. А было так: во время разливов священного Нила потоки воды иногда смывали границы участков земледельцев, а новые границы могли не совпасть со старыми. Налоги же крестьянами уплачивались в казну фараона пропорционально величине земельного надела. Измерением площадей пашни в новых границах после разлива занимались специальные люди. Именно в результате их деятельности и возникла новая наука, получившая развитие в Древней Греции. Там она и название получила, и приобрела практически современный вид. В дальнейшем термин стал интернациональным названием науки о плоских и объёмных фигурах.

Планиметрия – раздел геометрии, занимающийся изучением плоских фигур. Другим разделом науки является стереометрия, которая рассматривает свойства пространственных (объёмных) фигур. К таким фигурам относится и описываемая в этой статье – цилиндр.

Примеров присутствия предметов цилиндрической формы в повседневной жизни предостаточно. Цилиндрическую (гораздо реже – коническую) форму имеют почти все детали вращения — валы, втулки, шейки, оси и т.д. Цилиндр широко используется и в строительстве: башни, опорные, декоративные колонны. А кроме того посуда, некоторые виды упаковки, трубы всевозможных диаметров. И наконец – знаменитые шляпы, ставшие надолго символом мужской элегантности. Список можно продолжать бесконечно.

Видео:Теперь Я ЦИЛИНДР Редкая Мутация - The Eternal Cylinder Прохождение #6Скачать

Определение цилиндра как геометрической фигуры

Цилиндром (круговым цилиндром) принято называть фигуру, состоящую из двух кругов, которые при желании совмещаются с помощью параллельного переноса. Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».

Важно, что основания цилиндра всегда равны (если это условие не выполняется, то перед нами – усечённый конус, что-либо другое, но только не цилиндр) и находятся в параллельных плоскостях. Отрезки же, соединяющие соответствующие точки на кругах, параллельны и равны.

Совокупность бесконечного множества образующих — не что иное, как боковая поверхность цилиндра – один из элементов данной геометрической фигуры. Другая её важная составляющая – рассмотренные выше круги. Называются они основаниями.

Видео:ЭТО СУЩЕСТВО НЕ БОИТСЯ ЦИЛИНДРА ( The Eternal Cylinder )Скачать

Виды цилиндров

Самый простой и распространённый вид цилиндра – круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.

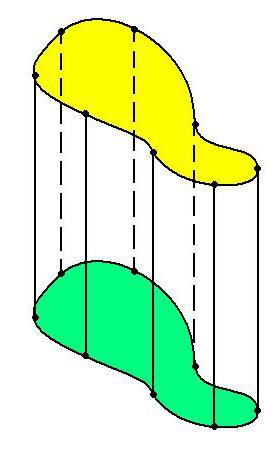
Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.

Читайте также: Конструктивные элементы крышки цилиндра

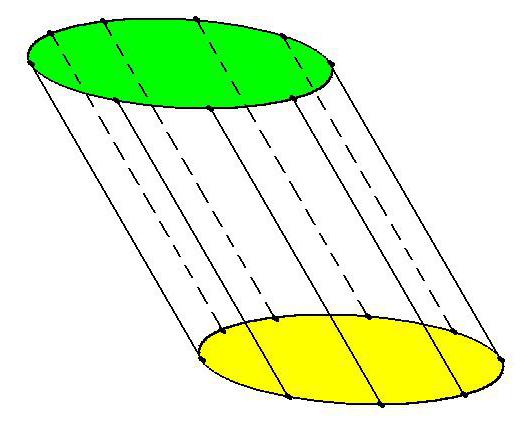
По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр – наклонный.

Видео:СЕКРЕТ ЦИЛИНДРА ( The Eternal Cylinder )Скачать

Что такое поверхность вращения

Прямой круговой цилиндр, без сомнения – самая распространённая поверхность вращения, используемая в технике. Иногда по техническим показаниям применяется коническая, шарообразная, некоторые другие типы поверхностей, но 99% всех вращающихся валов, осей и т.д. выполнены именно в форме цилиндров. Для того чтобы лучше уяснить, что такое поверхность вращения, можно рассмотреть, как же образован сам цилиндр.

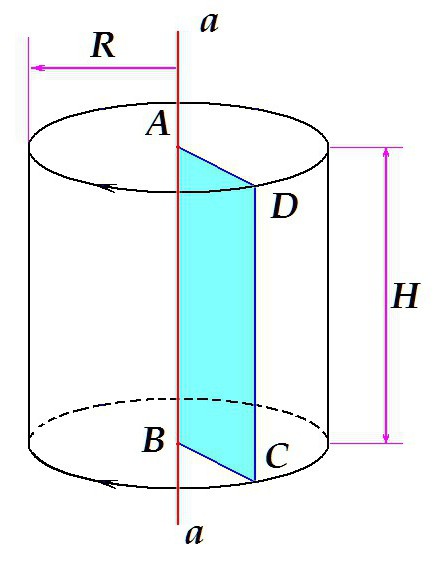
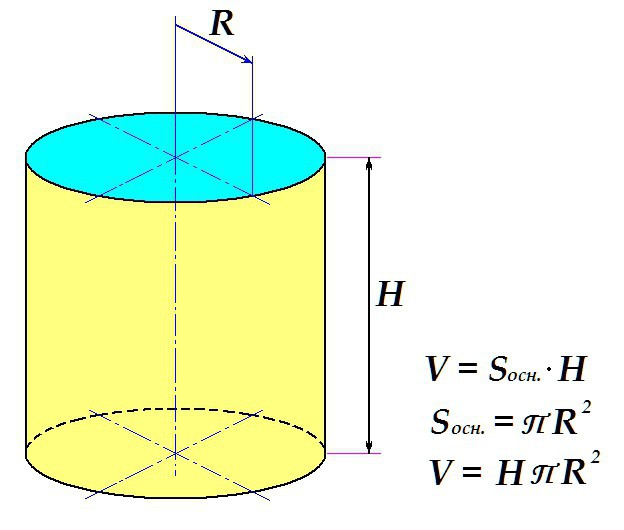
Допустим, имеется некая прямая a, расположенная вертикально. ABCD – прямоугольник, одна из сторон которого (отрезок АВ) лежит на прямой a. Если вращать прямоугольник вокруг прямой, как это показано на рисунке, объём, который он займёт, вращаясь, и будет нашим телом вращения – прямым круговым цилиндром с высотой H = AB = DC и радиусом R = AD = BC.

В данном случае, в результате вращения фигуры — прямоугольника — получается цилиндр. Вращая треугольник, можно получить конус, вращая полукруг – шар и т.д.

Видео:THE ETERNAL CYLINDER: ВСЕ "ЗА" И "ПРОТИВ" / ОБЗОР ИГРЫСкачать

Площадь поверхности цилиндра

Для того чтобы вычислить площадь поверхности обычного прямого кругового цилиндра, необходимо подсчитать площади оснований и боковой поверхности.

Вначале рассмотрим, как вычисляют площадь боковой поверхности. Это произведение длины окружности на высоту цилиндра. Длина окружности, в свою очередь, равняется удвоенному произведению универсального числа П на радиус окружности.

Площадь круга, как известно, равняется произведению П на квадрат радиуса. Итак, сложив формулы для площади определения боковой поверхности с удвоенным выражением площади основания (их ведь два) и произведя нехитрые алгебраические преобразования, получаем окончательное выражение для определения площади поверхности цилиндра.

Видео:ПЕРЕЛЕЗЛИ ЧЕРЕЗ ЦИЛИНДР ( The Eternal Cylinder )Скачать

Определение объёма фигуры

Объем цилиндра определяется по стандартной схеме: площадь поверхности основания умножается на высоту.

Таким образом, конечная формула выглядит следующим образом: искомое определяется как произведение высоты тела на универсальное число П и на квадрат радиуса основания.

Полученная формула, надо сказать, применима для решения самых неожиданных задач. Точно так же, как объем цилиндра, определяется, например, объём электропроводки. Это бывает необходимо для вычисления массы проводов.

Отличия в формуле только в том, что вместо радиуса одного цилиндра стоит делённый надвое диаметр жилы проводки и в выражении появляется число жил в проводе N. Также вместо высоты используется длина провода. Таким образом рассчитывается объем «цилиндра» не одного, а по числу проводков в оплётке.

Такие расчёты часто требуются на практике. Ведь значительная часть ёмкостей для воды изготовлена в форме трубы. И вычислить объем цилиндра часто бывает нужно даже в домашнем хозяйстве.

Однако, как уже говорилось, форма цилиндра может быть разной. И в некоторых случаях требуется рассчитать, чему равен объем цилиндра наклонного.

Отличие в том, что площадь поверхности основания умножают не на длину образующей, как в случае с прямым цилиндром, а на расстояние между плоскостями – перпендикулярный отрезок, построенный между ними.

Как видно из рисунка, такой отрезок равен произведению длины образующей на синус угла наклона образующей к плоскости.

Видео:ТРЕБУМЫ ОТБИРАЮТ У МОНСТРОВ МУТАЦИИ The Eternal CylinderСкачать

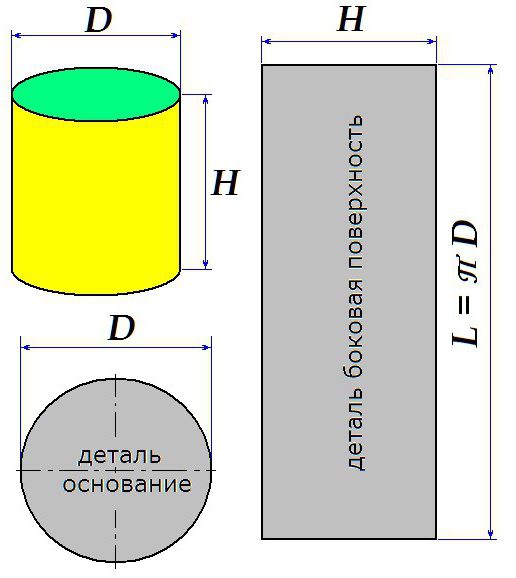
Как построить развёртку цилиндра

В некоторых случаях требуется выкроить развёртку цилиндра. На приведённом рисунке показаны правила, по которым строится заготовка для изготовления цилиндра с заданными высотой и диаметром.

Следует учитывать, что рисунок приведен без учёта швов.

Видео:БОГ ЗЕМЛИ И НАСТОЯЩАЯ СИЛА ЦИЛИНДРАСкачать

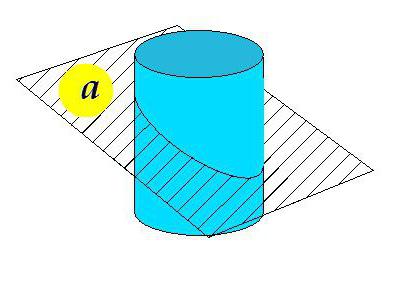
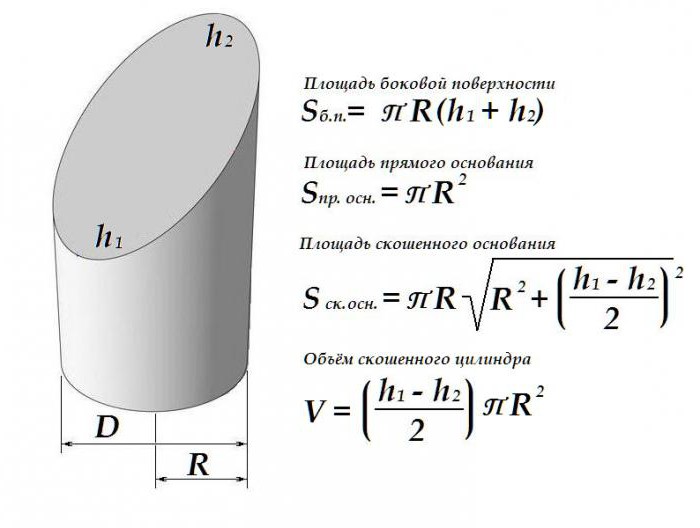
Отличия скошенного цилиндра

Представим себе некий прямой цилиндр, ограниченный с одной стороны плоскостью, перпендикулярной образующим. А вот плоскость, ограничивающая цилиндр с другой стороны, не перпендикулярна образующим и не параллельна первой плоскости.

На рисунке представлен скошенный цилиндр. Плоскость а под неким углом, отличным от 90° к образующим, пересекает фигуру.

Такая геометрическая форма чаще встречается на практике в виде соединений трубопроводов (колена). Но бывают даже здания, построенные в виде скошенного цилиндра.

Видео:ЯРОСТЬ ЦИЛИНДРА ( The Eternal Cylinder )Скачать

Геометрические характеристики скошенного цилиндра

Наклон одной из плоскостей скошенного цилиндра слегка изменяет порядок расчёта как площади поверхности такой фигуры, так и ее объёма.

🔥 Видео

НОВАЯ ТЕХНОЛОГИЯ ЦИЛИНДРА ( The Eternal Cylinder )Скачать

Требум TrebhumThe Eternal Cylinder вечный цилиндр. Знаете эту игру?Скачать