- Нахождение площади поверхности цилиндра: формула и задачи
- Формула вычисления площади цилиндра
- 1. Боковая поверхность
- 2. Основание
- 3. Полная площадь
- Примеры задач
- wiki.eduVdom.com
- Инструменты пользователя
- Инструменты сайта
- Боковая панель
- Цилиндр
- Цилиндр
- Определение
- Объем цилиндра
- Доказательство:
- Площадь боковой поверхности цилиндра
- Геометрические тела. Цилиндр.
- Формулы нахождения элементов цилиндра.
- Цилиндр: площадь боковой поверхности. Формула площади боковой поверхности цилиндра
- Понятие цилиндра
- Условные обозначения
- «Компоненты» стереометрической фигуры
- Основные формулы для работы с цилиндром
- Примеры с разобранным решением
- Задачи на закрепление материала
- 📸 Видео
Видео:Цилиндр - расчёт площади, объёма.Скачать

Нахождение площади поверхности цилиндра: формула и задачи
В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.
Видео:Видеоурок по математике "Цилиндр"Скачать

Формула вычисления площади цилиндра
1. Боковая поверхность
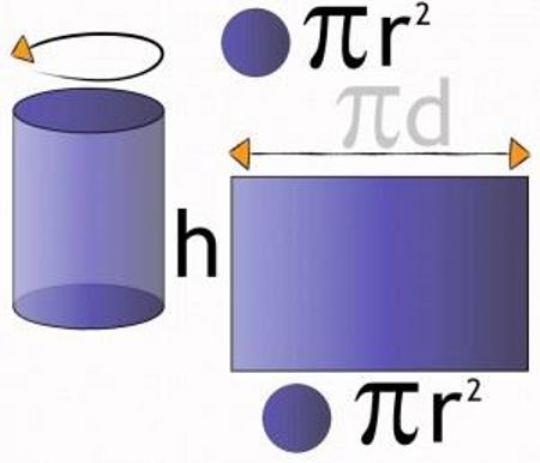
Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту.
Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом:
Примечание: в вычислениях значение числа π округляется до 3,14.
2. Основание
В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна:
Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:
3. Полная площадь
Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.:
S = 2 π R h + 2 π R 2 или S = 2 π R (h + R)
Видео:№544. Из квадрата, диагональ которого равна d, свернута боковая поверхность цилиндра.Скачать
Примеры задач
Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.
Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см 2 .
Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.
Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см 2 .
Видео:60. Площадь поверхности цилиндраСкачать

wiki.eduVdom.com
Инструменты пользователя
Инструменты сайта
Боковая панель
Стереометрия:
Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

Цилиндр
Цилиндром ( прямым круговым цилиндром ) называется тело, состоящее из двух кругов ( оснований цилиндра ), совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие при параллельном переносе точки этих кругов. Отрезки, соединяющие соответствующие точки окружностей оснований, называются образующими цилиндра.
Цилиндр — тело, которое ограничено цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями, пересекающими образующие данной поверхности.
Цилиндрическая поверхность — поверхность, которая образуется движением прямой линии вдоль некоторой кривой. Прямую называют образующей цилиндрической поверхности, а кривую линию — направляющей цилиндрической поверхности.
Боковая поверхность цилиндра — часть цилиндрической поверхности, которая ограничена параллельными плоскостями.
Основания цилиндра — части параллельных плоскостей, отсекаемые боковой поверхностью цилиндра.
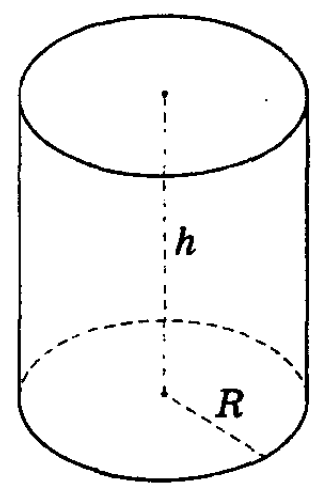
Цилиндр называется прямым (См.Рис.1), если его образующие перпендикулярны плоскостям оснований. В противном случае цилиндр называется наклонным.
Круговой цилиндр — цилиндр, основания которого являются кругами.
Прямой круговой цилиндр ( просто цилиндр ) – это тело, полученное при вращении прямоугольника вокруг одной из его сторон. См.Рис.1.
Радиус цилиндра – радиус его основания.
Образующая цилиндра — образующая цилиндрической поверхности.
Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.
Ось цилиндра параллельна его образующей и является осью симметрии цилиндра.
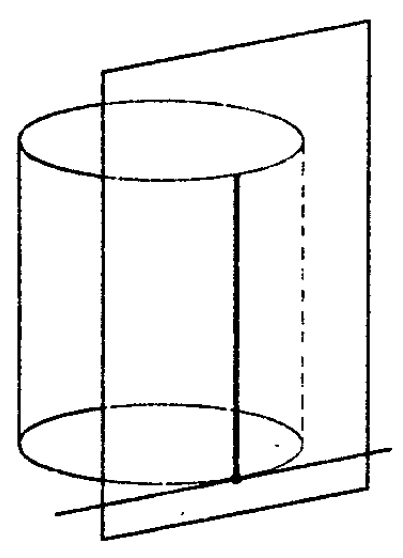
Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра. См.Рис.2.
Развёртка боковой поверхности цилиндра — прямоугольник со сторонами, равными высоте цилиндра и длине окружности основания.
Площадь боковой поверхности цилиндра — площадь развёртки боковой поверхности. $$S_ =2\pi\cdot rh$$ , где h – высота цилиндра, а r – радиус основания.
Читайте также: 41710b рабочий цилиндр сцепления
Площадь полной поверхности цилиндра — площадь, которая равна сумме площадей двух оснований цилиндра и его боковой поверхности, т.е. выражается формулой: $$S_ =2\pi\cdot r^2 + 2\pi\cdot rh = 2\pi\cdot r(r+h)$$ , где h – высота цилиндра, а r – радиус основания.
Объем всякого цилиндра равен произведению площади основания на высоту: $$V = S\cdot h$$ Объем круглого цилиндра: $$V=\pi r^2 \cdot h$$ , где (r — радиус основания).
Призма есть частный вид цилиндра (образующие параллельны боковым ребрам; направляющая — многоугольник, лежащий в основании). С другой стороны, произвольный цилиндр можно рассматривать как выродившуюся («сглаженную») призму с очень большим числом очень узких граней. Практически цилиндр неотличим от такой призмы. Все свойства призмы сохраняются и в цилиндре.
Видео:Цилиндр, конус, шар, 6 классСкачать

Цилиндр
Тела вращения – это объемные тела, которые возникают при вращении некой плоской фигуры, которая ограничена кривой и крутится вокруг оси, лежащей в той же плоскости. К телам вращения относятся цилиндр, конус и шар.
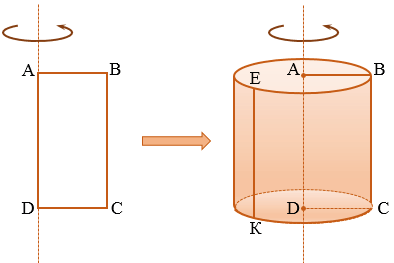
Цилиндр — это объемное тело, которое получается при вращении прямоугольника вокруг одной из его сторон.
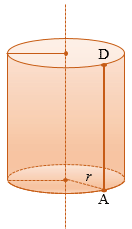
Возьмем прямоугольник АВСD. Будем вращать этот прямоугольник против часовой стрелки вокруг стороны АD.
Прямая АD — ось цилиндра.
Отрезок АD — высота цилиндра.
Основания цилиндра — два равных круга образованных при вращении сторон АВ и DC (круги равные, т.к. стороны АВ и DC равны как противоположные стороны прямоугольника).
Радиус цилиндра — радиус оснований цилиндра.
Цилиндрическая поверхность (или боковая поверхность цилиндра) — поверхность, образованная при вращении стороны ВС и состоящая из отрезков, параллельных оси цилиндра (АD).
Образующие цилиндра — отрезки, из которых составлена боковая поверхность цилиндра (на рисунке выше указаны образующие ВС и ЕК).
Определение
Объем цилиндра
Доказательство:
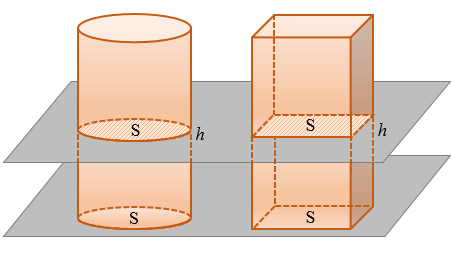
Дано: цилиндр с площадью основания S, высотой h и объемом V.
Доказать: V = Sh.
Доказательство:
Воспользуемся принципом Кавальери. Рассмотрим цилиндр и призму с площадями оснований, равными S, и высотами, равными h, «стоящие» на одной плоскости.
Любая секущая плоскость, параллельная плоскости, на которой стоят цилиндр и призма, дает в качестве сечения цилиндра круг площади S, а в качестве сечения призмы — многоугольник площади S. Значит, объем цилиндра равен объему призмы. Но объем призмы равен Sh. Поэтому и объем цилиндра равен Sh, т.е. V = Sh. Что и требовалось доказать.
Площадь боковой поверхности цилиндра
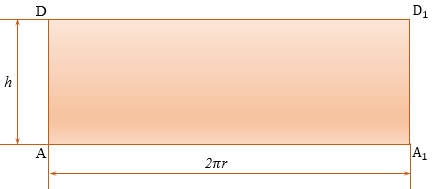
Рассмотрим цилиндр с радиусом r и высотой h.
Представим, что его боковую поверхность разрезали по одной из его образующих АD и развернули так, что получился прямоугольник АDА1D1, стороны АD и А1D1 которого являются двумя краями разреза боковой поверхности цилиндра. Этот прямоугольник называется разверткой боковой поверхности цилиндра.
Сторона АА1 прямоугольника АDА1D1 равна длине окружности основания, а сторона АD равна высоте цилиндра, т.е. АА1 = 2 r, АВ = h. Площадь прямоугольника равна произведению его смежных сторон, значит, площадь прямоугольника АDА1D1 равна 2 rh.
Площадь Sбок боковой поверхности цилиндра равна площади ее развертки, т.е. Sбок = 2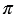 rh. rh. |
Поделись с друзьями в социальных сетях:
Видео:Нахождение площади боковой поверхности цилиндраСкачать

Геометрические тела. Цилиндр.
Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.
ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.
Цилиндрические сечения боковой поверхности кругового цилиндра.
Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.
Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.
Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.
Круговой цилиндр – цилиндр, основанием которого является круг.
Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.
Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.
Призма – это частный случай цилиндра.
Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Формулы нахождения элементов цилиндра.
Площадь боковой поверхности прямого кругового цилиндра:
Площадь полной поверхности прямого кругового цилиндра:
Объем прямого кругового цилиндра:
Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h1 и максимальной высоты h2.
Площадь боковой поверхности скошенного цилиндра:
Площадь оснований скошенного цилиндра:
Площадь полной поверхности скошенного цилиндра:
Объем скошенного цилиндра:
Sбок — площадь боковой поверхности;
Видео:площадь полной поверхности цилиндра.Скачать

Цилиндр: площадь боковой поверхности. Формула площади боковой поверхности цилиндра
При изучении стереометрии одной из главных тем становится «Цилиндр». Площадь боковой поверхности считается если не главной, то немаловажной формулой при решении геометрических задач. Однако важно помнить и определения, которые помогут сориентироваться в примерах и при доказательстве различных теорем.
Видео:8. Площадь боковой поверхности цилиндраСкачать

Понятие цилиндра
Вначале нужно рассмотреть несколько определений. Только после их изучения можно приступать к рассмотрению вопроса о формуле площади боковой поверхности цилиндра. На основе этой записи можно вычислить и иные выражения.
- Под цилиндрической поверхностью понимают плоскость, описываемую образующей, движущейся и остающейся параллельной заданному направлению, скользящей по имеющейся кривой.
- Имеется и второе определение: цилиндрическую поверхность образуют множество параллельных прямых, пересекающих заданную кривую.
- Образующей называют условно высоту цилиндра. При ее перемещении вокруг оси, проходящей через центр основания, получается обозначенное геометрическое тело.
- Под осью подразумевают прямую, проходящую через оба основания фигуры.
- Цилиндром называется стереометрическое тело, ограниченное пересекающимися боковой поверхностью и 2 параллельными плоскостями.
Существуют разновидности данной объемной фигуры:
Видео:Цилиндр. Площадь боковой и полной поверхности цилиндра.Скачать

Условные обозначения
- Радиус основания – R (он же заменяет аналогичную величину стереометрической фигуры).
- Образующая – L.
- Высота – H.
- Площадь основания – Sосн (иначе говоря, необходимо найти указанный параметр круга).
- Высоты скошенного цилиндра – h1,h2 (минимальная и максимальная).
- Площадь боковой поверхности – Sбок (если ее развернуть, то получится своего рода прямоугольник).
- Объем стереометрической фигуры – V.
- Площадь полной поверхности – S.
Видео:Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндраСкачать

«Компоненты» стереометрической фигуры
Когда изучается цилиндр, площадь боковой поверхности играет немаловажную роль. Связано это с тем, что данная формула входит в несколько других, более сложных. Поэтому необходимо быть хорошо подкованным в теории.
Основными составляющими фигуры являются:
Видео:ГЕОМЕТРИЯ 11 класс: Цилиндр. Площадь поверхностиСкачать

Основные формулы для работы с цилиндром
Для того чтобы ответить на вопрос, как найти площадь поверхности цилиндра, необходимо изучить основные «компоненты» стереометрической фигуры и формулы их нахождения. 
Видео:Площадь полной поверхности цилиндраСкачать

Примеры с разобранным решением
Необходимо узнать площадь боковой поверхности цилиндра. Дана диагональ сечения AC = 8 см (причем оно является осевым). При соприкосновении с образующей получается 








Видео:№538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевогоСкачать

Задачи на закрепление материала
Дан цилиндр. Площадь боковой поверхности используется в дальнейшем решении. Известны другие параметры. Площадь основания – Q, площадь осевого сечения – М. Необходимо найти S. Иными словами, полную площадь цилиндра. Дан цилиндр. Площадь боковой поверхности необходимо найти в одном из шагов решения задачи. Известно, что высота = 4 см, радиус = 2 см. Необходимо найти полную площадь стереометрической фигуры. Источник
📸 Видео
Цилиндр. Площадь боковой поверхности цилиндра. Объем цилиндра. Задание В6 из ЦТ 2021 #2021Скачать

ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ЦИЛИНДРА РАВНА 36п, А ДИАМЕТР ОСНОВАНИЯ РАВЕН 6. НАЙДИТЕ ВЫСОТУ ЦИЛИНДРАСкачать

ЗАДАЧА 769. МАТЕМАТИКА 6 класс. Площадь боковой поверхности цилиндра. ПРОЕКТ Домашнее обучение.Скачать

Задача на вычисление высоты цилиндраСкачать

11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать