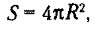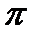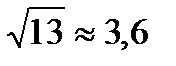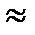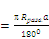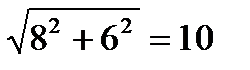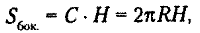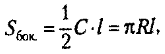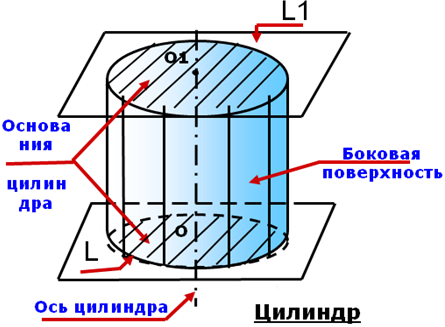
Основания цилиндра равны и лежат в параллельных плоскостях. Образующие цилиндра параллельны и равны.
Радиусом цилиндра называется радиус его оснований. Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований.
Цилиндр называется прямым, если образующая перпендикулярна плоскостям оснований. Высота прямого цилиндра равна длине образующей.
Сечение цилиндра плоскостью, проходящей через ось цилиндра называется осевым сечением. У прямого цилиндра осевое сечение. Представляет собой прямоугольник. Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.
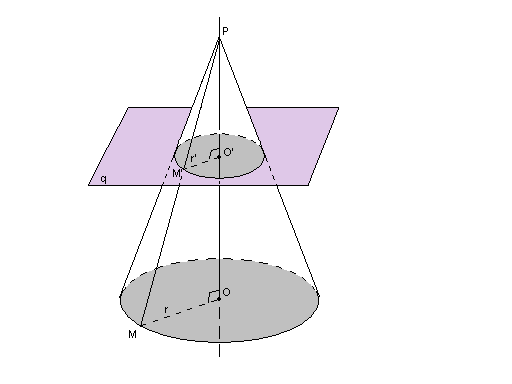
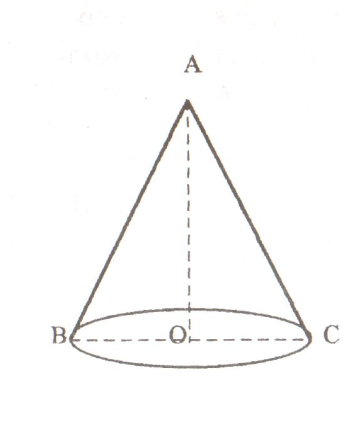
Конусом (круговым конусом) называется тело, которое состоит из круга – основания конуса; точки, не лежащей в плоскости этого круга – вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания.
Отрезки, соединяющие вершину конуса с точками окружности основания называются образующими конуса. Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания.
Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна
Осью прямого конуса называется прямая, содержащая его высоту.
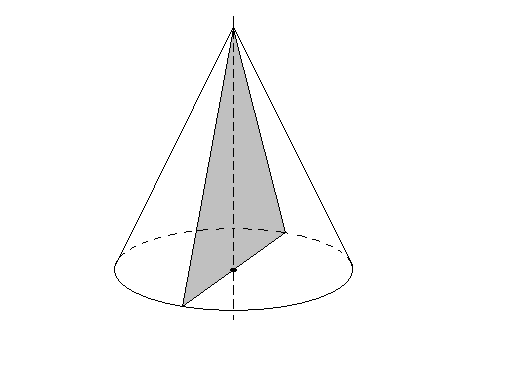
Сечение конуса плоскостью, проходящей через его ось называется осевым сечением.
Если секущая плоскость перпендикулярна
к оси конуса, то сечение конуса представляет собой круг с центром, расположенным на оси конуса.
Шаром называется тело, которое состоит из всех точек пространства,
находящихся на расстоянии, не большем данного, от данной точки. Эта точка
называется центром шара, а данное расстояние радиусом шара.
Граница шара называется шаровой поверхностью, или сферой.
Таким образом, точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, соединяющий центр шара с точкой шаровой поверхности, также называется радиусом.
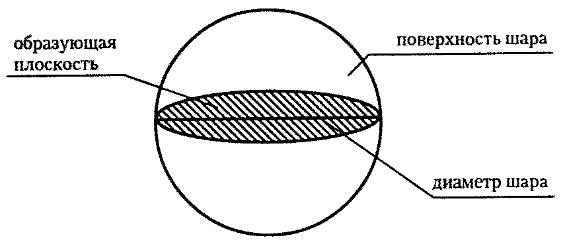
Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром. Концы любого диаметра называются диаметрально противоположными точками шара.
Шар, так же как цилиндр и конус, является телом вращения. Он получается при вращении полукруга вокруг его диаметра как о
Видео:Видеоурок по математике "Цилиндр"Скачать

Определение: Шар — это тело (объемная геометрическая фигура), полученное вращением полукруга вокруг его диаметра как оси. Развертки цилиндра и конуса
Разверткой геометрической фигуры называется изображение плоскости, ограничивающей фигуру, в одной плоскости листа по размерам фигуры. Развертка цилиндра приведена схематически. 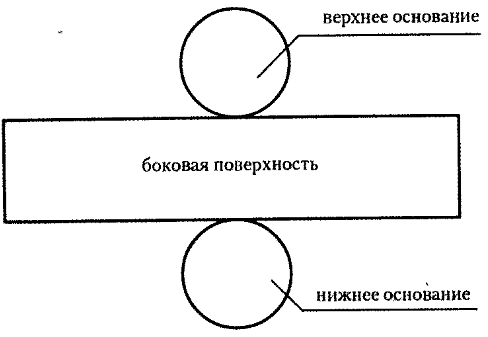
Читайте также: Розетка передняя триерного цилиндра
Площадь поверхности шара.
Площадь поверхности шара равна учетверенной площади большого круга шара. где R — радиус шара.
Решите задачи.
1. Радиус основания цилиндра 1,5 см,
высота- 4см. Чему равна диагональ
2. Осевое сечение цилиндра- квадрат,
Площадь которого36 дм 2 . Чему
равна площадь основания цилиндра?
Ответ: 9 дм 2 .
3.Квадрат со стороной 4 см вращается вокруг одной из своих сторон.
Чему равна площадь основания полученного тела?
Ответ: 16 cм 2 .
4. Наибольший угол между образующими
конуса 60 0 . Чему равен диаметр основания,
если образующая равна 7 см?
5.Высота цилиндра равна 8 см, радиус основания 1 см. Чему равна площадь осевого сечения?
6.В равностороннем цилиндре радиус основания равен 7,5 см. Чему
Видео:Нахождение площади боковой поверхности цилиндраСкачать

равна площадь осевого сечения?
7.Определите площадь боковой поверхности равностороннего цилиндра, высота которого 8 см.
Ответ: 64 cм 2
8.Проанализируйте решение и закончите его.
Боковая поверхность цилиндра втрое больше суммы площади его оснований. Найти периметр осевого сечения цилиндра, если радиус основания R=3 см.
1. Sбок=2 RH; Sосн= R 2
Sбок=3*2 Sосн; 2 RH=6 R 2 ; H=9см
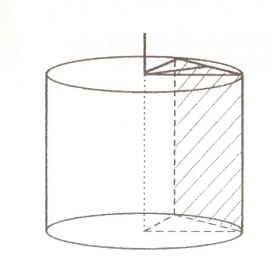
9. Высота цилиндра 20 см, радиус основания 10 см. Найдите площадь сечения, проведенного параллельно оси цилиндра на расстоянии 6 см от нее.
Указание. Найдите хорду, являющуюся стороной прямоугольника (сечения).
10. Высота цилиндра 12 см, радиус основания 7 см. Цилиндр пересечен плоскостью так, что в сечении оказался квадрат. Найдите расстояние от сечения до оси.
Ответ: (см).
11. ADCB – осевое сечение цилиндра, площадь которого равна 5 дм 2 . Найдите площадь боковой поверхности цилиндра.
12. Площадь полной поверхности цилиндра равна 24π см 2 , радиус основания – 2см. Чему равна высота цилиндра?
Выполнить задания в тетради
Решите задачи.
1. Наибольший угол между образующими конуса 60 0 . Чему равен диаметр основания, если образующая равна 7 см?
2. Площадь осевого сечения конуса равна 36 см 2 , высота конуса 12 см. Найдите радиус основания.
3. Чему равна площадь боковой поверхности равностороннего конуса, если образующая его равна 12 см?
4. Чему равна площадь боковой поверхности равностороннего конуса с радиусом основания 7 см?
5. Чему равна площадь боковой поверхности равностороннего конуса, если образующая его равна 12 см?
6. Определите площадь боковой поверхности усеченного конуса, если радиусы оснований равны 6 см и 8 см, образующая 5 см.
Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

7. В равностороннем конусе образующая равна 8 см. Чему равна площадь осевого сечения?
Читайте также: Как выглядит цилиндр в автомобиле
8.Проанализируйте решение задач и заполните пропуски.
1. Площадь основания конуса 75 см 2 ,
образующие наклоны к основанию по углом 60 0 . Найдите площадь боковой поверхности конуса (с точностью до целых).
Осевое сечение конуса – равнобедренный ∆АВС; ∆АВО – прямоугольного (т.к. АО — ___________________________________________________________________________________________________________________________________
находим l = 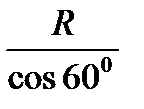
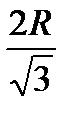
2) Sосн. = πR 2 =75 см 2 ; R 5 см;
3) откуда Sбок. ________________
Ответ:
9. Найдите площадь сечения конуса плоскостью, параллельной основанию и проходящей через середину высоты, если радиус основания равен 10 см.
Сделайте рисунок _____________________________________
10. В конусе радиус основания 4 см, образующая 10 см. Найдите центральный угол развертки его конической поверхности. Указание: длина дуги развертки вычисляется по формуле:
l
11. Образующая конуса составляет с плоскостью основания угол в 30 0 . Найдите дугу сектора, представляющего собой развертку боковой поверхности конуса.
12. Радиусы оснований усеченного конуса равны R и r, образующая составляет с плоскостью основания угол 45 0 . Найдите площадь осевого сечения.
13. Отношение площади основания конуса к площади осевого сечения равно π. Найдите угол наклона образующей к основанию.
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________Ответ: 45 0
14. Разверткой боковой поверхности конуса является сектор с дугой 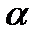
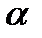
Видео:10 вариант ЕГЭ Ященко 2024 математика профильный уровень 🔴Скачать

1) Находим образующую конуса, она является радиусом (R) кругового сектора – развертки боковой поверхности конуса.
R = (см).
2) Длина дуги сектора равна длине окружности основания конуса и вычисляется по формуле l =2πr, где r = 6 см, т.е. l = 12π см.
3) Из формулы l = 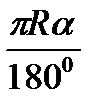
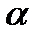
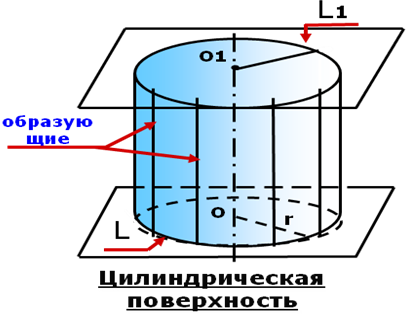
Цилиндром ( круговым цилиндром)называется тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.

Круги называются основаниями цилиндра, а отрезки, соединяющиесоответствующие точки окружностей
кругов – образующими цилиндра.
Основания цилиндра равны и лежат в параллельных плоскостях. Образующие цилиндра параллельны и равны.
Радиусом цилиндра называется радиус его оснований. Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований.
Цилиндр называется прямым, если образующая перпендикулярна плоскостям оснований. Высота прямого цилиндра равна длине образующей.
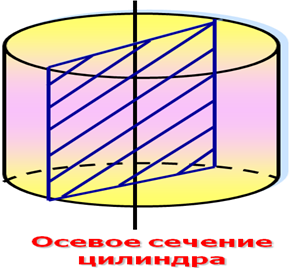
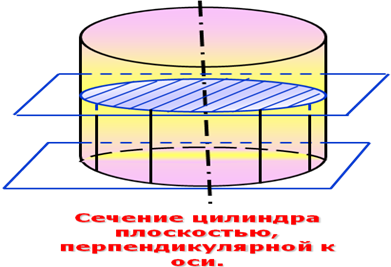
Сечение цилиндра плоскостью, проходящей через ось цилиндра называется осевым сечением. У прямого цилиндра осевое сечение. Представляет собой прямоугольник. Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.
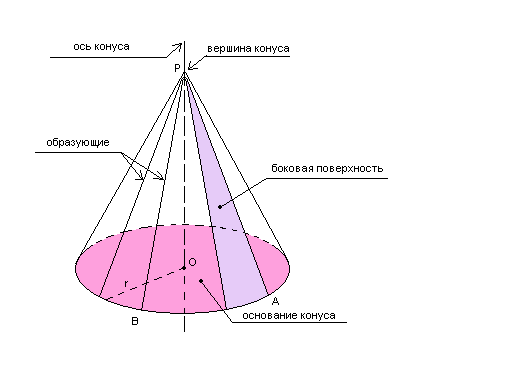
Конусом (круговым конусом) называется тело, которое состоит из круга – основания конуса; точки, не лежащей в плоскости этого круга – вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания.
Читайте также: Центральный тормозной цилиндр ваз 2114
Отрезки, соединяющие вершину конуса с точками окружности основания называются образующими конуса. Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания.
Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна
Осью прямого конуса называется прямая, содержащая его высоту.
Сечение конуса плоскостью, проходящей через его ось называется осевым сечением.
Если секущая плоскость перпендикулярна
к оси конуса, то сечение конуса представляет собой круг с центром, расположенным на оси конуса.
Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

Шаром называется тело, которое состоит из всех точек пространства,
находящихся на расстоянии, не большем данного, от данной точки. Эта точка
называется центром шара, а данное расстояние радиусом шара.
Граница шара называется шаровой поверхностью, или сферой.
Таким образом, точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, соединяющий центр шара с точкой шаровой поверхности, также называется радиусом.
Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром. Концы любого диаметра называются диаметрально противоположными точками шара.
Шар, так же как цилиндр и конус, является телом вращения. Он получается при вращении полукруга вокруг его диаметра как о
Определение: Шар — это тело (объемная геометрическая фигура), полученное вращением полукруга вокруг его диаметра как оси. Развертки цилиндра и конуса
Разверткой геометрической фигуры называется изображение плоскости, ограничивающей фигуру, в одной плоскости листа по размерам фигуры. Развертка цилиндра приведена схематически. 
Площади боковой поверхности цилиндра и конуса.
Правило. Площадь боковой поверхности цилиндраравна произведению длины окружности основания и высоты цилиндра. где C — длина окружности, H — высота цилиндра, R — радиус окружности основания.
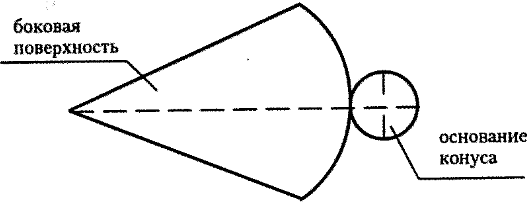
Площадь боковой поверхности конуса равна произведению половины длины окружности основания и образующей конуса.
где C — длина окружности основания, l — длина образующей конуса, R — радиус основания.
Площадь поверхности шара.
Площадь поверхности шара равна учетверенной площади большого круга шара. где R — радиус шара.
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
📸 Видео
ЕГЭ 2022 математика задача 4 вариант 2Скачать

ОТКУДА? Как найти площадь боковой поверхности конуса? Развёртка конуса | Математика с ДетекторомСкачать

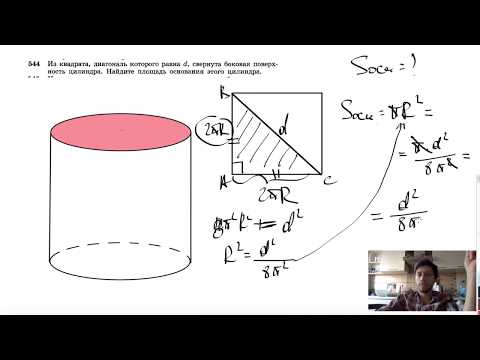
№544. Из квадрата, диагональ которого равна d, свернута боковая поверхность цилиндра.Скачать
9 вариант ЕГЭ Ященко 2024 математика профильный уровень 🔴Скачать

Решение прикладных задач на вычисление площади поверхностиСкачать

60. Площадь поверхности цилиндраСкачать

№538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевогоСкачать

Профильный ЕГЭ 2024 математика Ященко. Вариант 9Скачать

Новый Профильный ЕГЭ 2024. Математика разбор Ященко вариант 9Скачать

№540. Высота цилиндра на 12 см больше его радиуса, а площадь полной поверхности равна 288π см2Скачать

РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

ЗАДАЧА 769. МАТЕМАТИКА 6 класс. Площадь боковой поверхности цилиндра. ПРОЕКТ Домашнее обучение.Скачать

62. Площадь поверхности конусаСкачать

11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

ГЕОМЕТРИЯ 11 класс: Цилиндр. Площадь поверхностиСкачать