- 5.4.1 Цилиндр. Основание, высота, боковая поверхность, образующая, развертка
- Что такое цилиндр: определение, элементы, виды, варианты сечения
- Определение цилиндра
- Основные элементы цилиндра
- Геометрические тела. Цилиндр.
- Формулы нахождения элементов цилиндра.
- Геометрические тела. Цилиндр.
- Формулы нахождения элементов цилиндра.
- Цилиндр
- Определение
- Объем цилиндра
- Доказательство:
- Площадь боковой поверхности цилиндра
- 🎦 Видео
Видео:Видеоурок по математике "Цилиндр"Скачать

5.4.1 Цилиндр. Основание, высота, боковая поверхность, образующая, развертка
Видеоурок: Цилиндр. Решение задач
Лекция: Цилиндр. Основание, высота, боковая поверхность, образующая, развертка
Цилиндр
Давайте представим, известную нам, окружность, у которой есть центр в точке О. А теперь из каждой точки этой окружности проведем прямые, перпендикулярные данной окружности. Вся поверхность, которую образуют данные прямые – это и есть цилиндрическая плоскость.
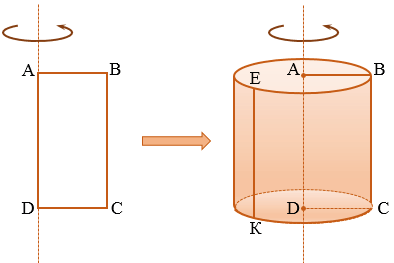
Как еще можно получить цилиндр? Попробуйте взять лист бумаги, закрепить его вертикально и начать быстро вращать вокруг его оси. В таком случае Вы заметите, что быстро вращающийся лист будет рисовать некое объемное тело, которое и называется цилиндром.
У цилиндра есть два основания (верхнее и нижнее) и оба они имеют форму окружности. Перпендикулярная к основаниям плоскость, называется боковой поверхностью цилиндра.
Возьмите лист бумаги и соедините его противоположные края – Вы как раз получите боковую поверхность цилиндра. А что будет, если этот лист снова развернуть? Он снова будет иметь форму прямоугольника. Это значит, что боковая поверхность цилиндра – это прямоугольная плоскость.
Площадь поверхности цилиндра
Как уже писалось ранее, цилиндр состоит из оснований и боковой поверхности. Это значит, что для нахождения всей площади нам нужно знать площадь боковой поверхности цилиндров и основания.
Так как в основаниях лежит окружность, найти площадь оснований можно по следующей формуле: S = 2πR 2 .
Для тех, кто хорошо выучил тему об окружностях, возразят, что в формуле не должно быть цифры «2», однако из-за того, что основания в виде окружности два, и они равны между собой, площадь достаточно умножить на «2».
А теперь перейдем к площади поверхности. Как говорилось ранее, боковая поверхность создана прямоугольником, поэтому достаточно умножить длину его на ширину. Ширина – это высота цилиндра, а длина – это длина окружности, поэтому площадь боковой поверхности: S = 2πRH.
А значит, общая площадь поверхности цилиндра:
Читайте также: Нет компрессии во всех цилиндрах киа сид
Видео:Цилиндр - расчёт площади, объёма.Скачать

Что такое цилиндр: определение, элементы, виды, варианты сечения
В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Видео:Задача на вычисление высоты цилиндраСкачать

Определение цилиндра
Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.
Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.
Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O1O2 на 180° или прямоугольников ABO2O1/O1O2CD вокруг стороны O1O2 на 360°.
Видео:Егэ.11кл. Объём первого цилиндра равен 12 м³, у второго цилиндра высота в 3 раза больше,а основаниеСкачать

Основные элементы цилиндра
- Основания цилиндра – два одинаковых по размеру/площади круга с центрами в точках O1 и O2.
- R – радиус оснований цилиндра, отрезки AD и BC – диаметры (d).
- O1O2 – ось симметрии цилиндра, одновременно является его высотой (h).
- l (AB, CD) – образующие цилиндра и одновременно с этим стороны прямоугольника ABCD. Равны высоте фигуры.
Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.
- длина данного прямоугольника равна длине окружности основания цилиндра ( 2πR );
- ширина равна высоте/образующей цилиндра.
Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.
Видео:Цилиндр, длина окружности, высота, площадь боковой поверхности.Скачать

Геометрические тела. Цилиндр.
Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.
ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.
Цилиндрические сечения боковой поверхности кругового цилиндра.
Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.
Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.
Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.
Круговой цилиндр – цилиндр, основанием которого является круг.
Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.
Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.
Призма – это частный случай цилиндра.
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Формулы нахождения элементов цилиндра.
Площадь боковой поверхности прямого кругового цилиндра:
Площадь полной поверхности прямого кругового цилиндра:
Объем прямого кругового цилиндра:
Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h1 и максимальной высоты h2.
Площадь боковой поверхности скошенного цилиндра:
Площадь оснований скошенного цилиндра:
Площадь полной поверхности скошенного цилиндра:
Объем скошенного цилиндра:
Sбок — площадь боковой поверхности;
Видео:🔴 Даны два цилиндра. Радиус основания и высота ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Геометрические тела. Цилиндр.
Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.
ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.
Цилиндрические сечения боковой поверхности кругового цилиндра.
Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.
Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.
Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.
Круговой цилиндр – цилиндр, основанием которого является круг.
Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.
Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.
Призма – это частный случай цилиндра.
Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Формулы нахождения элементов цилиндра.
Площадь боковой поверхности прямого кругового цилиндра:
Площадь полной поверхности прямого кругового цилиндра:
Объем прямого кругового цилиндра:
Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h1 и максимальной высоты h2.
Площадь боковой поверхности скошенного цилиндра:
Площадь оснований скошенного цилиндра:
Площадь полной поверхности скошенного цилиндра:
Объем скошенного цилиндра:
Sбок — площадь боковой поверхности;
Видео:ЕГЭ 2022 математика задача 4 вариант 2Скачать

Цилиндр
Тела вращения – это объемные тела, которые возникают при вращении некой плоской фигуры, которая ограничена кривой и крутится вокруг оси, лежащей в той же плоскости. К телам вращения относятся цилиндр, конус и шар.
Цилиндр — это объемное тело, которое получается при вращении прямоугольника вокруг одной из его сторон.
Возьмем прямоугольник АВСD. Будем вращать этот прямоугольник против часовой стрелки вокруг стороны АD.
Прямая АD — ось цилиндра.
Отрезок АD — высота цилиндра.
Основания цилиндра — два равных круга образованных при вращении сторон АВ и DC (круги равные, т.к. стороны АВ и DC равны как противоположные стороны прямоугольника).
Радиус цилиндра — радиус оснований цилиндра.
Цилиндрическая поверхность (или боковая поверхность цилиндра) — поверхность, образованная при вращении стороны ВС и состоящая из отрезков, параллельных оси цилиндра (АD).
Образующие цилиндра — отрезки, из которых составлена боковая поверхность цилиндра (на рисунке выше указаны образующие ВС и ЕК).
Определение
Объем цилиндра
Доказательство:
Дано: цилиндр с площадью основания S, высотой h и объемом V.
Доказать: V = Sh.
Доказательство:
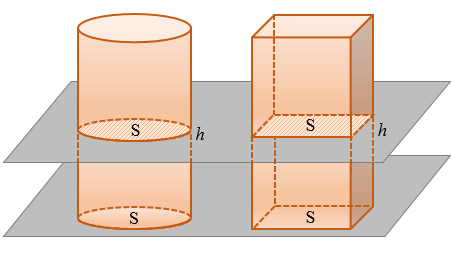
Воспользуемся принципом Кавальери. Рассмотрим цилиндр и призму с площадями оснований, равными S, и высотами, равными h, «стоящие» на одной плоскости.
Любая секущая плоскость, параллельная плоскости, на которой стоят цилиндр и призма, дает в качестве сечения цилиндра круг площади S, а в качестве сечения призмы — многоугольник площади S. Значит, объем цилиндра равен объему призмы. Но объем призмы равен Sh. Поэтому и объем цилиндра равен Sh, т.е. V = Sh. Что и требовалось доказать.
Площадь боковой поверхности цилиндра
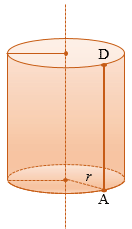
Рассмотрим цилиндр с радиусом r и высотой h.
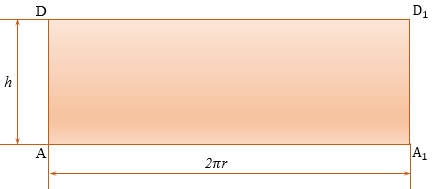
Представим, что его боковую поверхность разрезали по одной из его образующих АD и развернули так, что получился прямоугольник АDА1D1, стороны АD и А1D1 которого являются двумя краями разреза боковой поверхности цилиндра. Этот прямоугольник называется разверткой боковой поверхности цилиндра.
Сторона АА1 прямоугольника АDА1D1 равна длине окружности основания, а сторона АD равна высоте цилиндра, т.е. АА1 = 2 r, АВ = h. Площадь прямоугольника равна произведению его смежных сторон, значит, площадь прямоугольника АDА1D1 равна 2 rh.
Площадь Sбок боковой поверхности цилиндра равна площади ее развертки, т.е. Sбок = 2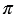 rh. rh. |
Поделись с друзьями в социальных сетях:
🎦 Видео
ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

Нахождение площади боковой поверхности цилиндраСкачать

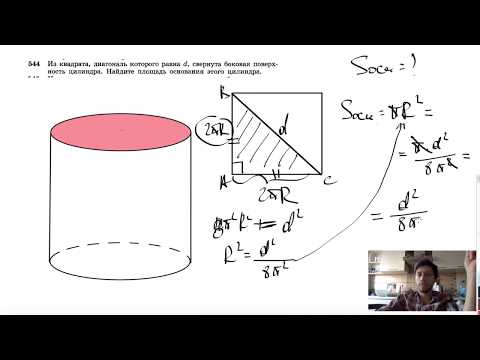
№544. Из квадрата, диагональ которого равна d, свернута боковая поверхность цилиндра.Скачать
Вычисление высоты конуса - типовое заданиеСкачать

8. Площадь боковой поверхности цилиндраСкачать

Задание 2 ЕГЭ профиль Цилиндр Боковая поверхностьСкачать

№538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевогоСкачать

Цилиндр. Площадь боковой поверхности цилиндра. Площадь полной поверхности цилиндра. Площадь сеченияСкачать

Стереометрия. ЕГЭ. Правильная четырехугольная призма описана около цилиндра. Найдите высоту цилиндраСкачать

№537. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длинеСкачать

№531. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельнойСкачать