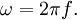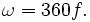Углова́я ско́рость — векторная величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:
,
а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.
Единица измерения угловой скорости, принятая в системах СИ и СГС) — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]). В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли, просто «вручную» подсчитывая число оборотов за единицу времени.
Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью определяется формулой:
где — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) r от оси вращения можно считать так: v = rω. Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.
- В случае плоского вращения, то есть когда все векторы скоростей точек тела лежат (всегда) в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.
- Производная угловой скорости по времени есть угловое ускорение.
- Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю).
- Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчета, однако в разных инерциальных системах отсчета может различаться ось или центр вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
- В случае движения одной единственной точки в трехмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:
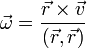
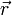
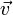
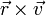

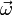
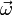
- В случае равномерного вращательного движения (то есть движения с постоянным вектором угловой скорости) декартовы координаты точек вращающегося так тела совершают гармонические колебания с угловой (циклической) частотой, равной модулю вектора угловой скорости.
- При измерении угловой скорости в оборотах в секунду (об/с), модуль угловой скорости равномерного вращательного движения совпадает с частотой вращения f, измеренной в герцах (Гц) (то есть в таких единицах
).
- В случае использования обычной физической единицы угловой скорости — радианов в секунду — модуль угловой скорости связан с частотой вращения так:
- Наконец, при использовании градусов в секунду связь с частотой вращения будет:
- См. также
- Смотреть что такое «Частота вращения» в других словарях:
- Единицы измерения скорости при вращательном движении
- Частота вращения: формула
- Номинальная скорость вращения
- Угловая скорость
- Угловая скорость в конкретных случаях
- Как определить угловую скорость
- Угол поворота и период обращения
- Циклическая частота вращения (обращения)
- Переход от угловой к линейной скорости
- Видео
- Видео
Видео:Разбираем чертеж детали ➤ Технические требования ➤ Допуски и посадки размеровСкачать

См. также
Wikimedia Foundation . 2010 .
Смотреть что такое «Частота вращения» в других словарях:
частота вращения ВК — частота вращения ветроколеса Угол, проходимый лопастью ВК за единицу времени, измеренный в оборотах в единицу времени или в радианах. [ГОСТ Р 51237 98] Тематики ветроэнергетика Синонимы частота вращения ветроколеса EN rotation speed … Справочник технического переводчика
Читайте также: Сборка главного вала кпп т 25
частота вращения — частота вращения … Справочник технического переводчика
Частота вращения — 3.113 Частота вращения число оборотов в единицу времени. Источник: ГОСТ Р МЭК 1029 2 4 96: Машины переносные электрические. Частные тр … Словарь-справочник терминов нормативно-технической документации
частота вращения — sukimosi dažnis statusas T sritis automatika atitikmenys: angl. rotating speed; rotation frequency; rotational speed vok. Drehgeschwindigkeit, f; Rotationsgeschwindigkeit, f rus. скорость вращения, f; частота вращения, f pranc. fréquence de… … Automatikos terminų žodynas
частота вращения — sūkių dažnis statusas T sritis Standartizacija ir metrologija apibrėžtis Kūno sukimosi apie tam tikrą ašį dažnis, išreiškiamas sūkių skaičiumi per vienetinį laiko tarpą. atitikmenys: angl. rotating frequency; rotating speed; rotation frequency;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Частота вращения w — 69. Частота вращения w Угловая скорость вращения поворотной части крана в установившемся режиме движения. Определяется при наибольшем вылете с рабочим грузом при установке крана на горизонтальной площадке и скорости ветра не более 3 м/с на высоте … Словарь-справочник терминов нормативно-технической документации
частота вращения — sukimosi dažnis statusas T sritis fizika atitikmenys: angl. rotation frequency vok. Rotationsfrequenz, f; Umlauffrequenz, f rus. частота вращения, f pranc. fréquence de rotation, f … Fizikos terminų žodynas
ЧАСТОТА ВРАЩЕНИЯ — величина, равная отношению числа оборотов, совершённых телом, ко времени вращения. Обозначается обычно п. Единица Ч. в. (в СИ) с 1. Внесистемные единицы об/мин и об/с … Большой энциклопедический политехнический словарь
частота вращения — rotation frequency Число оборотов вращающегося звена в единицу времени. Шифр IFToMM: Раздел: СТРУКТУРА МЕХАНИЗМОВ … Теория механизмов и машин
частота вращения ротора (вала) ГТД в режиме сопровождения — частота вращения режима сопровождения Частота вращения ротора ГТД при запуске в момент отключения пускового устройства. [ГОСТ 23851 79] Тематики двигатели летательных аппаратов Синонимы частота вращения режима сопровождения … Справочник технического переводчика
Видео:Допуски и посадки для чайников и начинающих специалистовСкачать

Единицы измерения скорости при вращательном движении
Единицы измерения скорости при поступательном движении
Единицы, часто применяемые в судовой электротехнике
При поступательном движении скорость движущихся масс называется «линейная скорость», обозначается латинской буквой «υ» и измеряется в «м/с» ( метр в секунду ) или «м/мин» ( метр в минуту ).Например, скорость подъёма груза электропривода лебёдки υ = = 30 м/мин.
На практике применяют внесистемные ( не соответствующие системе СИ ) едини-
цы измерения скорости, например, километр в час ( км/ч ), узел = 1852 м /ч ( 1852 м – дли-
При измерении скорости вращающихся масс применяют два наименования скоро-
1. «частота вращения», обозначается латинской буквой «n» и измеряется в
«об/мин» ( оборот в минуту ). Например, частота вращения двигателя n = 1500 об/мин.
Эта единица скорости – внесистемная, т.к. в ней используется внесистемная едини
ца времени, а именно – минута ( в системе СИ время измеряется в секундах ).
Тем не менее эта единица до сих пор широко применяется на практике. Например, в паспортных данных электродвигателей скорость вала указывается именно в об/ мин.
2. «угловая скорость», обозначается латинской буквой «ω» и измеряется в
«рад/с» ( радиан в секунду ) или, что одно и то же, с( секунда в минус первой степени ).
Например, угловая скорость электродвигателя ω = 157 с.
Напомним, что радиан – вторая, кроме знакомого нам пространственного градуса
( º ), единица измерения углового расстояния, равная 360º / 2π = 360 / 2*3,14 = 57º36′ ( пять
десят семь градусов и 36 минут ).
Впервые возникла в расчетах, где часто встречалось число 360º / 2π.
Эта единица скорости – системная, т.к. в ней используется системная единица вре-
На практике надо уметь быстро переходить от одной единицы скорости к другой и наоборот.
Поэтому выведем соотношение между этими двумя единицами.
Угловая скорость ( через частоту вращения ):
ω = 2 πn / 60 = n / ( 60 / 2 π ) = n / 9,55 ≈ n / 10 ( В.1 ).
Частота вращения ( через угловую скорость ):
n = 60 ω / 2 π = 60 ω / 2*3,14 = 9,55 ω ≈ 10 ω ( В.2 ).
В паспорте электродвигателя указана номинальная скорость вала n = 1500 об/мин.
Найти угловую скорость вала этого электродвигателя.
ω =n / 9,55 = 1500 / 9,55 = 157 ≈ 150 с.
В паспорте электродвигателя указана угловая скорость вала электродвигателя
Найти частоту вращения вала этого электродвигателя.
Читайте также: Почему выходит из строя подшипник первичного вала
n = 9,55 ω = 9,55*314 = 3000 ≈ 3140 об/ мин.
Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Частота вращения: формула
Количество повторений каких-либо событий или их возникновения за одну единицу таймера называется частотой. Это физическая величина измеряется в герцах – Гц (Hz). Она обозначается буквами ν, f, F, и есть отношение количества повторяющихся событий к промежутку времени, в течение которого они произошли.
При обращении предмета вокруг своего центра можно говорить о такой физической величине, как частота вращения, формула:
- N – количество оборотов вокруг оси или по окружности,
- t – время, за которое они были совершены.
В системе СИ обозначается как – с-1 (s-1) и именуется как обороты в секунду (об/с). Применяют и другие единицы вращения. При описании вращения планет вокруг Солнца говорят об оборотах в часах. Юпитер делает одно вращение в 9,92 часа, тогда как Земля и Луна оборачиваются за 24 часа.
Видео:Как определить вращение насоса НШ /3 способа/Скачать

Номинальная скорость вращения
Прежде, чем дать определение этому понятию, необходимо определиться, что такое номинальный режим работы какого-либо устройства. Это такой порядок работы устройства, при котором достигаются наибольшая эффективность и надёжность процесса на продолжении длительного времени. Исходя из этого, номинальная скорость вращения – количество оборотов в минуту при работе в номинальном режиме. Время, необходимое для одного оборота, составляет 1/v секунд. Оно называется периодом вращения T. Значит, связь между периодом обращения и частотой имеет вид:
К сведению. Частота вращения вала асинхронного двигателя – 3000 об./мин., это номинальная скорость вращения выходного хвостовика вала при номинальном режиме работы электродвигателя.
Как найти или узнать частоты вращений различных механизмов? Для этого применяется прибор, который называется тахометр.
Видео:Ременная передача. Урок №3Скачать

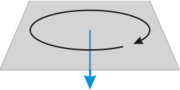
Угловая скорость
Когда тело движется по окружности, то не все его точки движутся с одинаковой скоростью относительно оси вращения. Если взять лопасти обычного бытового вентилятора, которые вращаются вокруг вала, то точка расположенная ближе к валу имеет скорость вращения больше, чем отмеченная точка на краю лопасти. Это значит, у них разная линейная скорость вращения. В то же время угловая скорость у всех точек одинаковая.
Угловая скорость представляет собой изменение угла в единицу времени, а не расстояния. Обозначается буквой греческого алфавита – ω и имеет единицу измерения радиан в секунду (рад/с). Иными словами, угловая скорость – это вектор, привязанный к оси обращения предмета.
Формула для вычисления отношения между углом поворота и временным интервалом выглядит так:
- ω – угловая скорость (рад./с);
- ∆ϕ – изменение угла отклонения при повороте (рад.);
- ∆t – время, затраченное на отклонение (с).
Обозначение угловой скорости употребляется при изучении законов вращения. Оно употребляется при описании движения всех вращающихся тел.
Угловая скорость в конкретных случаях
На практике редко работают с величинами угловой скорости. Она нужна при конструкторских разработках вращающихся механизмов: редукторов, коробок передач и прочего.
Вычислить её, применяя формулу, можно. Для этого используют связь угловой скорости и частоты вращения.
- π – число, равное 3,14;
- ν – частота вращения, (об./мин.).
В качестве примера могут быть рассмотрены угловая скорость и частота вращения колёсного диска при движении мотоблока. Часто необходимо уменьшить или увеличить скорость механизма. Для этого применяют устройство в виде редуктора, при помощи которого понижают скорость вращения колёс. При максимальной скорости движения 10 км/ч колесо делает около 60 об./мин. После перевода минут в секунды это значение равно 1 об./с. После подстановки данных в формулу получится результат:
К сведению. Снижение угловой скорости часто требуется для того, чтобы увеличить крутящий момент или тяговое усилие механизмов.
Как определить угловую скорость
Принцип определения угловой скорости зависит от того, как происходит движение по окружности. Если равномерно, то употребляется формула:
Если нет, то придётся высчитывать значения мгновенной или средней угловой скорости.
Величина, о которой идёт разговор, векторная, и при определении её направления используют правило Максвелла. В просторечии – правило буравчика. Вектор скорости имеет одинаковое направление с поступательным перемещением винта, имеющего правую резьбу.
Рассмотрим на примере, как определить угловую скорость, зная, что угол поворота диска радиусом 0,5 м меняется по закону ϕ = 6*t:
Вектор ω меняется из-за поворота в пространстве оси вращения и при изменении значения модуля угловой скорости.
Читайте также: Причины не морозит холодильник с одним компрессором
Видео:Физика.Узнать за 2 минуты.Основные понятия.Что такое частотаСкачать

Угол поворота и период обращения
Рассмотрим точку А на предмете, вращающимся вокруг своей оси. При обращении за какой-то период времени она изменит своё положение на линии окружности на определённый угол. Это угол поворота. Он измеряется в радианах, потому что за единицу берётся отрезок окружности, равный радиусу. Ещё одна величина измерения угла поворота – градус.
Когда в результате поворота точка А вернётся на своё прежнее место, значит, она совершила полный оборот. Если её движение повторится n-раз, то говорят о некотором количестве оборотов. Исходя из этого, можно рассматривать 1/2, 1/4 оборота и так далее. Яркий практический пример этому – путь, который проделывает фреза при фрезеровании детали, закреплённой в центре шпинделя станка.
Внимание! Угол поворота имеет направление. Оно отрицательное, когда вращение происходит по часовой стрелке и положительное при вращении против движения стрелки.
Если тело равномерно продвигается по окружности, можно говорить о постоянной угловой скорости при перемещении, ω = const.
В этом случае находят применения такие характеристики, как:
- период обращения – T, это время, необходимое для полного оборота точки при круговом движении;
- частота обращения – ν, это полное количество оборотов, которое совершает точка по круговой траектории за единичный временной интервал.
Интересно. По известным данным, Юпитер обращается вокруг Солнца за 12 лет. Когда Земля за это время делает вокруг Солнца почти 12 оборотов. Точное значение периода обращения круглого гиганта – 11,86 земных лет.
Видео:Как определить мощность, частоту вращения, двигателя без бирки или шильдика самому и простоСкачать

Циклическая частота вращения (обращения)
Скалярная величина, измеряющая частоту вращательного движения, называется циклической частотой вращения. Это угловая частота, равная не самому вектору угловой скорости, а его модулю. Ещё её именуют радиальной или круговой частотой.
Циклическая частота вращения – это количество оборотов тела за 2*π секунды.
У электрических двигателей переменного тока это частота асинхронная. У них частота вращения ротора отстаёт от частоты вращения магнитного поля статора. Величина, определяющая это отставание, носит название скольжения – S. В процессе скольжения вал вращается, потому что в роторе возникает электроток. Скольжение допустимо до определённой величины, превышение которой приводит к перегреву асинхронной машины, и её обмотки могут сгореть.
Устройство этого типа двигателей отличается от устройства машин постоянного тока, где токопроводящая рамка вращается в поле постоянных магнитов. Большое количество рамок вместил в себя якорь, множество электромагнитов составили основу статора. В трёхфазных машинах переменного тока всё наоборот.
При работе асинхронного двигателя статор имеет вращающееся магнитное поле. Оно всегда зависит от параметров:
- частоты питающей сети;
- количества пар полюсов.
Скорость вращения ротора состоит в прямом соотношении со скоростью магнитного поля статора. Поле создаётся тремя обмотками, которые расположены под углом 120 градусов относительно друг друга.
Видео:6.2 Кинематический расчет приводаСкачать
Переход от угловой к линейной скорости
Существует различие между линейной скоростью точки и угловой скоростью. При сравнении величин в выражениях, описывающих правила вращения, можно увидеть общее между этими двумя понятиями. Любая точка В, принадлежащая окружности с радиусом R, совершает путь, равный 2*π*R. При этом она делает один оборот. Учитывая, что время, необходимое для этого, есть период Т, модульное значение линейной скорости точки В находится следующим действием:
Так как ω = 2*π*ν, то получается:
Следовательно, линейная скорость точки В тем больше, чем дальше от центра вращения находится точка.
К сведению. Если рассматривать в качестве такой точки города на широте Санкт-Петербурга, их линейная скорость относительно земной оси равна 233 м/с. Для объектов на экваторе – 465 м/с.
Числовое значение вектора ускорения точки В, движущейся равномерно, выражается через R и угловую скорость, таким образом:
а = ν2/ R, подставляя сюда ν = ω* R, получим: а = ν2/ R = ω2* R.
Это значит, чем больше радиус окружности, по которой движется точка В, тем больше значение её ускорения по модулю. Чем дальше расположена точка твердого тела от оси вращения, тем большее ускорение она имеет.
Поэтому можно вычислять ускорения, модули скоростей необходимых точек тел и их положений в любой момент времени.
Понимание и умение пользоваться расчётами и не путаться в определениях помогут на практике вычислениям линейной и угловой скоростей, а также свободно переходить при расчётах от одной величины к другой.
Видео:Определение направления вращения НШСкачать

Видео
🔥 Видео
Насос с изменяемой частотой вращения вала. Grundfos управление со смартфона?Скачать

ИЗМЕРЯЙ ОБОРОТЫ ВАЛА,ТЕЛЕФОНОМ# ЛАЙФХАК,КАК ИЗМЕРИТЬ ОБОРОТЫ ДВИГАТЕЛЯ# ВЕРСИЯ 2Скачать

Принцип работы редуктора. Виды редукторов. Курсовая.Скачать

4.1 Расчет посадок с натягомСкачать

ТЕХНИКА БЕЗОПАСНОСТИ. Вид Грубейшего Нарушения ТРЕБОВАНИЙ ТБ при работе на СТАНКАХ.Скачать

Выбираем допуски и посадки ➤ Система вала и отверстияСкачать

Моделирование ускоренного вращения вала в ANSYS WorkbenchСкачать

Читаем и создаем чертежи - Допуски. Посадки. КвалитетыСкачать
ПОСЛЕ ЭТОГО АКПП не будет дергаться и пинаться при трогании!Скачать

Чтение машиностроительных чертежей деталей. Технические требования и обозначенияСкачать

Как правильно эксплуатировать насос НШ /ТОП-5 ошибок/Скачать


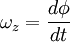
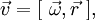
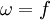 ).
).