Частота вращения вала центробежного насоса

Видео:Как работает центробежный насос? Основные типы конструкций центробежных насосовСкачать

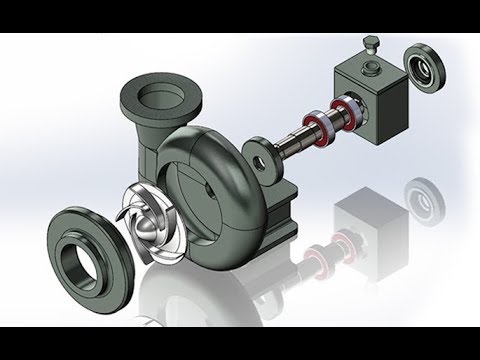
Регулирование скорости вращения рабочего колеса

Регулирование скорости

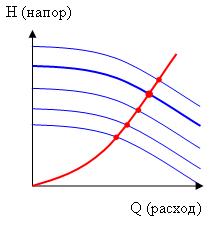
При регулировании (изменении) скорости вращения рабочего колеса центробежного насоса, рабочая точка смещается по красной кривой характеристики сети (гидросистемы): вверх – при увеличении частоты вращения, вниз – при уменьшении частоты вращения.

Недостатки работы центробежного насоса на пониженной скорости:

• ухудшается смазка и охлаждение уплотнений
• увеличивается вероятность забивания насоса и появления осадка

При регулировании скорости вращения рабочего колеса с помощью преобразователя частоты (ПЧ) необходимо:

• обеспечить быстрый разгон насоса до минимальной скорости (как правило, эта скорость соответствует 30 Гц на выходе ПЧ)
• при автоматическом регулировании скорости не опускаться ниже этой частоты.

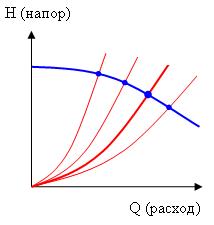
Дроссельное регулирование

При регулировании расхода с помощью задвижки (вентиля) рабочая точка будет смещаться по синей кривой характеристики насоса: влево – при закрытии задвижки, вправо – при открытии задвижки.

Недостатки дроссельного регулирования расхода:

• Повышается давление в системе (напор)
• Снижается КПД системы.

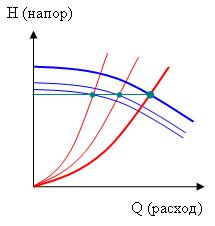
Поддержание постоянного напора (давления)

Если одновременно закрывать задвижку и уменьшать скорость вращения рабочего колеса, то можно обеспечить поддержание постоянного напора при снижении расхода (рабочая точка смещается влево по зелёной прямой линии).

Поддержание постоянного расхода

Если одновременно открывать задвижку и уменьшать скорость вращения рабочего колеса, то можно обеспечить поддержание постоянного расхода при снижении напора (рабочая точка смещается вниз по зелёной прямой линии).

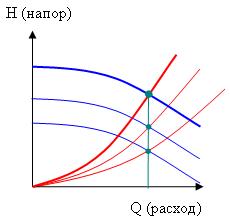
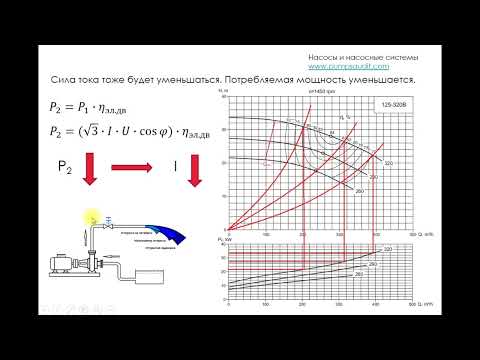
Зависимость напора, расхода и потребляемой мощности от частоты вращения

Расход (подача) пропорционален частоте вращения рабочего колеса центробежного насоса:

Напор (давление) пропорционален квадрату частоты вращения:

Мощность, потребляемая насосом, пропорциональна кубу частоты вращения:

Видео:Центробежный насос устройство конструкцияСкачать

Регулирование подачи насоса.

Основной задачей регулирования подачи насоса является подача в сеть расхода Q(м 3 /ч), заданного определенным графиком. При этом характеристики насоса, такие как Н(напор), p(давление), N(мощность) и η(коэффициент полезного действия) имеют тенденцию изменяться.

Однако сеть трубопроводов и потребители накладывают на некоторые из параметров определенные условия. Например насосы должны создавать определенные потребителем расход и давление, отвечающее гидравлическим свойствам системы трубопроводов.

Содержание статьи

Компрессоры в некоторых случаях работают на сеть с переменным Q, но должны обеспечить постоянное давление р (например, пневматический инструмент) в других случаях они работают с постоянным Q при переменном р.

Таким образом возможны различные варианты регулирования подачи. Самые актуальные способы регулирования подачи насоса рассмотрены в этой статье.

Видео:Наглядное изменение частоты работы насосаСкачать

Дроссельное регулирование при постоянной частоте оборотов.

Предположим, что насос подключен так, как показано на схеме.

Отложим на графике характеристики напора, мощности и КПД центробежного насоса при постоянном числе оборотов.

На этом же графике изобразим характеристику трубопроводной сети, на которую работает насос. При этом считается, что регулирующий дроссель открыт полностью.

Установившийся режим работы центробежного агрегата возможен только если напор насоса равен напору, расходуемому в системе. Это равенство наблюдается в точке а.

В случае прикрытия дросселя на напорной трубе точка а передвинется по характеристике влево и займет положение а / , задав новые значения параметров Q / , H / , N / . Дальнейшее перекрывание дросселя вызывает смещение характеристики трубопроводной системы ещё больше вверх, и точка а передвигается в точку а // , дающую значения параметров Q // , H // , N // и т.д.

Следовательно, дроссельное регулирование при постоянной частоте вращения достигается введением дополнительного гидравлического сопротивления в сеть трубопроводов машины.

Поскольку наибольшая подача достигается при полностью открытом дросселе (точка а), дроссельное регулирование применяют только с целью уменьшения подачи. Энергетическая эффективность такого регулирования низка, но благодаря своей простоте этот способ широко применяется.

При дроссельном регулировании центробежных машин, подающих жидкость, дроссель располагают на напорной трубе. Если расположить его на всасывающей трубе, то при глубоком регулировании может возникать кавитация.

Изменение частоты вращения вала

В тех случаях, когда имеется возможность изменять частоту вращения вала двигателя, приводящего в движение центробежную машину, целесообразно воспользоваться этим вариантом.

Насос подключен к трубопроводу так же, как и в предыдущей схеме и работает при частотах вращения n1, n2, n3, причем n1

Видео:Загадки центробежного насосаСкачать

Зависимость подачи, напора и мощности от числа оборотов насоса

Одним из приемов расширения области применения центробежных насосов является изменение их числа оборотов.

Скорость вращения ротора центробежного насоса существенно влияет на его основные показатели: подачу Q, напор Н и мощность на валу насоса N.

При изменении скорости вращения ротора центробежного насоса с n1 до n2 оборотов в минуту подача, напор и мощность на валу изменяются в соответствии с уравнениями:

Читайте также: Электрокоса с жестким валом

Эти соотношения называются законом пропорциональности.

Из приведенных уравнений закона пропорциональности следует:

По этим формулам производится пересчет характеристик насоса на новое число оборотов.

Для построения новой характеристики насоса при частоте вращения n2 следует на заданной характеристике насоса Н=f (Q) при частоте вращения n1 взять несколько произвольных точек при различных подачах Q и соответствующих им значений Н. Далее, используя законы пропорциональности, следует вычислить значения расхода Q2 и напора Н2. По новым значениям Q2 и Н2 построить новые точки и через них провести новую характеристику насоса Н=f (Q) при новом числе оборотов n2.

При построении кривой кпд (η-Q) пользуются тем, что кпд насоса при изменении числа оборотов в довольно широких пределах остается практически постоянным. Уменьшение числа оборотов до 50% практически не вызывает изменений кпд насоса.

Определение частоты вращения вала насоса, обеспечивающей подачу заранее обусловленного расхода воды.

Частоту вращения n2, соответствующую нужному расходу Q2 следует находить, используя законы пропорциональности, приведенные выше.

При этом следует знать, что если взять на заданной характеристике насоса Н при частоте вращения n1, то она будет характеризоваться определенными значениями расхода Q1 и напора Н1. Далее, при уменьшении частоты вращения до n2, используя законы пропорциональности, можно получить новые значения координат этой точки. Ее положение будет характеризоваться значениями Q2 и Н2. Если еще уменьшить частоту вращения до n3, то после перерасчета получим новые значения Q3 и Н3, характеризующие точку и т.д.

Если соединить все точки плавной кривой, то получим параболу, выходящую из начала координат. Следовательно, при изменении частоты вращения вала насоса значение напора и подачи насоса будут характеризоваться положением точек, лежащих на параболе, выходящей из начала координат и называемой параболой подобных режимов.

Для определения Q1 и Н1, входящих в соотношения

и , необходимо построить параболу подобных режимов по уравнению:

Так как парабола должна пройти через точку с координатами Q2 и Н2, постоянный коэффициент параболы k может быть найден по формуле:

Н2 берется с характеристики трубопровода при заданном расходе Q2 или вычисляется по формуле:

где Нг – геометрическая высота подъема; S – коэффициент сопротивления трубопровода.

Для построения параболы нужно задаться несколькими произвольными значениями Q. Точка пересечения параболы с характеристикой насоса Н при числе оборотов n1 определяет значения Q1 и H1, и частота вращения определяется, как

Потребная скорость вращения ротора насоса может быть определена аналитически:

для водопроводных центробежных насосов по формуле:

где n1 и nпотр – соответственно нормальное и потребное число оборотов в минуту;

Нг – геометрическая высота подъема;

n и m – соответственно число ниток водовода и число насосов;

S – сопротивление одной нитки водовода;

для фекальных центробежных насосов по формуле:

Видео:Как работает торцевое уплотнение? / Центробежный насосСкачать

О расчете рабочих характеристик центробежных насосов с частотным регулированием производительности

К.т.н. Г.В. Ледуховский, доцент, заместитель заведующего кафедрой «Тепловые электрические станции»;
к.т.н. А.А. Поспелов, доцент кафедры «Тепловые электрические станции»;ФГБОУВПО «Ивановский государственный энергетический университет им. В.И. Ленина», г. Иваново

Нормативно-техническая документация, регламентирующая порядок построения рабочих характеристик насосов [1, 4], касается случая работы приводных электродвигателей при номинальном числе оборотов ротора. Поэтому на практике при построении рабочих характеристик насосов при частотном регулировании их производительности используют методики, описанные в специальной технической литературе [2, 3]. Степень точности полученных характеристик зависит от объема экспериментальных данных и используемой методики их обработки.

При проведении функциональных испытаний насосов, оснащенных блоками частотно-регулируемого привода, в условиях промышленной эксплуатации редко удается выполнить более одного опыта при каждом числе оборотов ротора, поскольку необходимо обеспечить требуемый режим работы сети. При стендовых испытаниях насосов такого ограничения не существует. Это обстоятельство следует учитывать при выборе методики обработки опытных данных в целях получения комплекса рабочих характеристик.

В большинстве литературных источников [2, 3] для построения рабочих характеристик насосов при частотном регулировании производительности предложен подход, основанный на использовании формул пропорциональности. Формулы пропорциональности, полученные исходя из положений теории подобия динамических машин, отражают изменение рабочих параметров насоса при изменении числа оборотов ротора, диаметра рабочего колеса и т.п. Так, если известны рабочие характеристики насоса при номинальном числе оборотов ротора, то при его изменении рабочие параметры могут быть определены по выражениям

где Q — объемная подача насоса, м 3 /ч; Н — напор насоса, м вод. ст.; N — мощность на валу насоса, кВт; n — число оборотов ротора насоса, об./мин; η_об, η_г, η — соответственно объемный, гидравлический и полный КПД насоса; индекс «н» указывает на значение параметра в номинальном режиме работы насоса, т.е. при номинальном числе оборотов ротора.

Читайте также: Компрессор для закачки воздуха в баллоны для дайвинга

Для практических расчетов формулы (1) применимы лишь условно, поскольку функции изменения η_об и η_г в зависимости от числа оборотов ротора в большинстве случаев отсутствуют. В связи с этим рекомендуется [2, 3] использовать упрощенные выражения, полученные в предположении, что гидравлический и объемный КПД насоса остаются неизменными при любой частоте вращения ротора:

Нужно отметить, что погрешность, вносимая в расчет пренебрежением неравенства КПД насоса при изменении числа оборотов ротора, тем меньше, чем меньше изменение самого числа оборотов ротора.

Для дальнейших рассуждений обозначим математическую модель (2) как «модель 1». Сопоставим для примера результаты расчета рабочих характеристик по модели 1 с данными, полученными в ходе натурных испытаний насоса типа 1Д-800-56 (рис. 1). Здесь и далее будем рассматривать только случаи при n 3 /ч, и η_нн, ед., — соответственно число оборотов ротора, подача и КПД насоса в рабочей точке насоса при номинальном числе оборотов ротора; n и Q — изменившиеся значения числа оборотов ротора и подачи насоса; k — коэффициент пропорциональности, значение которого принимается по рекомендациям (от 0,28 до 1,54 в зависимости от типа насоса [6]) либо определяется из результатов испытаний.

Следует отметить, что величина η_нн*[1-(Q/Q)^ 2,3 ] в выражении (3) определяет номинальную рабочую характеристику насоса по КПД в общем случае. Ее использование для практических расчетов приводит к большим погрешностям. Более точным является использование зависимости, описывающей реальную номинальную характеристику КПД, полученную в испытаниях, т.е. некоторой функции F_η (Q/Q_нн), вид которой для каждого типа насосов индивидуален. Кроме того, при обработке результатов испытаний конкретного насоса с использованием зависимости (3) зачастую не достигается требуемая степень точности, что приводит к необходимости введения второго параметра идентификации — степени относительного числа оборотов ротора (η/η_нн) в выражении (3). Обозначим эту степень через a. С учетом этого выражение (3) перепишется в следующем виде:

В рамках этого подхода напорная характеристика насоса при изменении числа оборотов ротора может быть аппроксимирована зависимостью

Здесь функция F_H (Q/Q_нн) описывает номинальную рабочую напорную характеристику насоса; степень а, по опыту обработки результатов натурных испытаний насосов, совпадает со степенью относительного числа оборотов ротора в выражении для КПД.

Уравнение для расчета мощности на валу насоса при изменении числа оборотов ротора при использовании выражений (4) и (5) определится как

где g=9,81 м/с 2 — ускорение свободного падения; ρ — средняя плотность воды в насосе, кг/м 3 .

Для расчета по выражениям (4)-(6) (назовем эту модель моделью 2) необходимо знать параметры идентификации математической модели k и а.

При расчете с использованием номинальных рабочих характеристик и отсутствии экспериментальных данных в соответствии с рекомендациями [6] следует принять а=2 и значение k в пределах от 0,28 до 1,54 в зависимости от типа насоса. Более точные рабочие характеристики получаются при использовании для идентификации модели экспериментальных данных. Ясно, что получение уравнений, описывающих рабочие характеристики насоса в подобном виде, возможно только при обработке большого объема опытных данных. Для рассмотренного выше примера с насосом 1Д-800-56 получены значения а=2,3 и k=0,3. Результаты расчета с использованием модели 2 представлены на рис. 2.

Анализ результатов использования модели 2 позволяет заключить следующее:

■ расчеты по модели 2 приводят к более точным значениям напора и мощности, чем значения, полученные с использованием модели 1; так, по опыту расчетов, для модели 2 средняя разница между расчетными и экспериментальными значениями не превышает 11%, однако при недостаточности экспериментальных данных это расхождение может достигать более 30%;

■ характеристика КПД насоса, рассчитанная по модели 2, при уменьшении числа оборотов ротора деформируется вдоль оси ординат; максимальное значение КПД уменьшается при отклонении числа оборотов ротора от номинального значения, подача, при которой КПД имеет максимальное значение, остается неизменной. Расчетные и опытные значения КПД соотносятся между собой с отклонением не более 5% (относительных);

■ относительное число оборотов ротора входит в выражение расчета напора насоса в степени, обычно превышающей 2 (в рассмотренном примере а=2,3), что противоречит основным положениям теории насосов. Это обстоятельство, по-видимому, связано с тем, что модель 2 не учитывает изменения подачи насоса в подобных режимах его работы.

Читайте также: Как отцентровать диск сцепления без первичного вала ваз 2109

Таким образом, модель 2 следует считать аппроксимационной (статистической) математической моделью. Используя эту модель, можно с высокой степенью точности обработать опытные данные. Однако точность аппроксимации напрямую зависит от количества опытных точек, поэтому для использования этой модели требуется проведение испытаний насосов в широких диапазонах изменения параметров. Пересчет номинальных рабочих характеристик насосов по модели 2 при отсутствии экспериментальных данных приводит к относительно большим погрешностям.

Учитывая представленные результаты анализа, возникла необходимость в разработке более универсальной математической модели, позволяющей с достаточной точностью прогнозировать характер рабочих характеристик насосов при переменном числе оборотов ротора даже в случае отсутствия большого объема экспериментальных данных. Такая модель получена авторами путем развития модели 1 в целях более полного учета физической природы процессов, протекающих в насосах при изменении числа оборотов ротора, а также обобщения многих экспериментальных данных. Основные расчетные выражения, составляющие полученную математическую модель (назовем ее моделью 3), следующие:

где Q, м 3 /ч — объемная подача насоса; Н, м вод.ст. — напор насоса; N, кВт – мощность на валу насоса; η_н, ед. — полный КПД насоса; n, об./мин — число оборотов ротора насоса; А — вспомогательный комплекс; g, м/с 2 — ускорение свободного падения, р, кг/м 3 — средняя плотность воды в насосе; d_M и d_вс, м — диаметры соответственно напорного и всасывающего патрубков насоса; r — параметр идентификации модели; индекс «н» указывает на значение параметра при номинальном числе оборотов ротора.

Имея характеристики насоса при номинальном (или ином) числе оборотов ротора (О_н, Н_н, η_н) в функциональном, табличном или графическом виде и задав один параметр идентификации г, можно рассчитать рабочие характеристики при отклонении числа оборотов ротора. Параметр идентификации модели r может быть определен по результатам испытаний либо задан исходя из его физического смысла. По опыту использования модели значение r обычно близко к r=0,5.

На рис. 3 представлены результаты расчетов с использованием модели 3 для рассмотренного выше примера с насосом 1Д-800-56. В данном случае отклонение расчетных параметров от опытных данных составило 4,8%.

Модель 3 более полно отражает закономерности физических процессов, протекающих в насосах при изменении числа оборотов ротора, чем модель 1. По сложности расчетов и универсальности модель 3 сопоставима с моделью 2, однако требует значительно меньшего объема исходной информации. Настройка модели 3 по результатам эксперимента проще, чем настройка модели 2, поскольку в нее входит только один параметр идентификации. Из рассмотренных моделей модель 3 позволяет получить наиболее точные результаты (в целом по опыту использования отклонение между опытными и расчетными значениями показателей не превышает 7%).

Использование модели 3 при обработке результатов функциональных испытаний четырех насосов Omega 200-520А производства KSB Actiengesellschaft (Германия), четырех насосов 1Д-800-56, четырех насосов СЭ-800-55-11 и девяти насосов СЭ-500-70-16, оснащенных блоками частотно-регулируемого привода производства General Electric Company (США), показало, что возможно значительное сокращение количества рассматриваемых режимов каждого насоса (для каждого насоса выполнено от 4 до 9 опытов при отклонении числа оборотов ротора от номинального значения), а среднее отклонение расчетных значений параметров от опытных данных составило 2,6%.

Литература

1. Методические указания по составлению и содержанию энергетических характеристик оборудования тепловых электростанций — РД 34.09.155-93: разраб. «Фирма по наладке, совершенствованию технологии и эксплуатации электростанций и сетей ОРГРЭС», утв. Министерством топлива и энергетики России 22.09.93, ввод. в действие с 01.12.93.

2. Черкасский В. М. Насосы, вентиляторы, компрессоры: учебник для теплоэнергетических специальностей вузов / В.М. Черкасский — 2-е изд., перераб. и доп. — М.: Энергоатомиздат, 1984. — 416 с.

3. Турк В.И. Насосы и насосные станции: учебник для вузов /В.И. Турк, А.В. Минаев, В.Я. Карелин. — М.: Стройиздат, 1976. — 304 с.

4. ГОСТ 6134-87. Насосы динамические. Методы испытаний (с изм. 1 и 2). — Взамен ГОСТ 6134-71: утв. Госстандартом СССР 29.06.1987: ввод в действие с 01.07.1987.

5. Энергетические насосы: каталог / ЦИНТИХИМНЕФТЕМАШ. — М.: Типография НИИМАШ, 1974. — 50 с.

6. Колесников А. И. Энергосбережение в промышленных и коммунальных предприятиях: учеб. пособие /А.И. Колесников, М.Н. Федоров, Ю.М. Варфоломеев; под общ. ред. М.Н. Федорова. — М.: ИНФРА-М, 2005. — 124 с.

• Свежие записи
  • Чем отличается двухтактный мотор от четырехтактного
  • Сколько масла заливать в редуктор мотоблока
  • Какие моторы бывают у стиральных машин
  • Какие валы отсутствуют в двухвальной кпп
  • Как снять стопорную шайбу с вала

  
  

  источники:

  https://evakuatorinfo.ru/chastota-vrascheniya-vala-tsentrobezhnogo-nasosa

  📽️ Видео

  Выставить соосность при помощи проволоки? Показываем, как это сделать подручными средствами.Скачать

  

  Центробежный насос - устройство и принцип работыСкачать

  

  Формулы подобия центробежных насосовСкачать

  

  Мощностная характеристика насосаСкачать

  

  Пересчет характеристик центробежных насосов на вязкие среды. Видеозапись вебинараСкачать

  

  Частотное регулирование насосаСкачать

  

  326) АВТОМАТИКА Предельный регулятор частоты вращения дизеля ( вопросы Госов и мкк )Скачать

  

  Рабочая точка насосаСкачать

  

  Вихревые насосы. Устройство и принцип работыСкачать

  

  Как работает центробежный насос с магнитной муфтойСкачать

  

  Расчет насосной установки. Хелп часть 3. Изменение характеристики насосаСкачать

  

  Практическое занятие 2: Основы расчета прогиба вала центробежного насоса в ANSYS WorkbenchСкачать

  

  Как проверить циркуляционный насос ??? ЛЕГКО И ПРОСТО !!!Скачать

  

  Центробежные насосыСкачать

  

  Ремонт насосов Биение валов и муфт Центровка валовСкачать