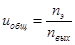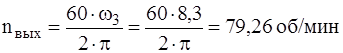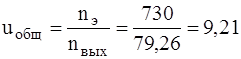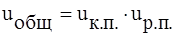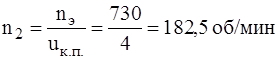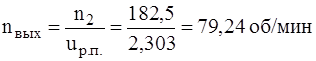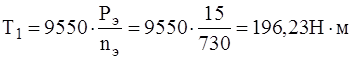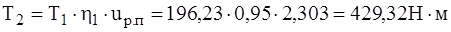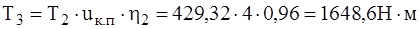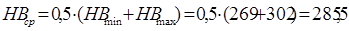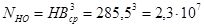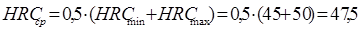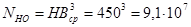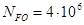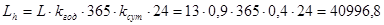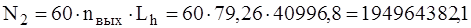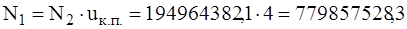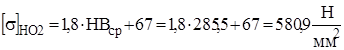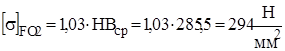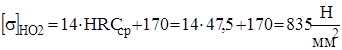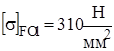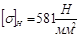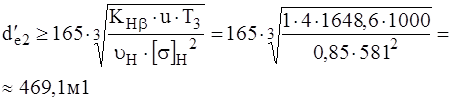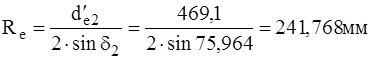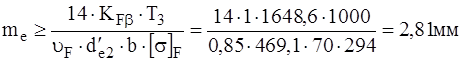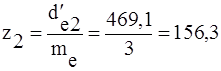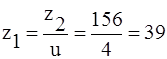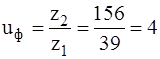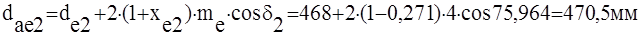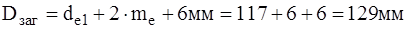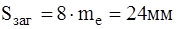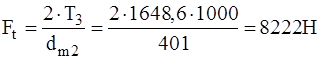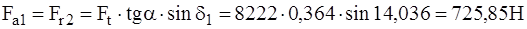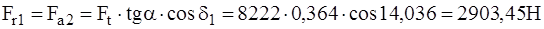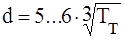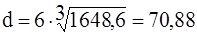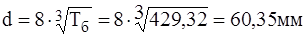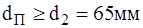Частота вращения валов формула

Количество повторений каких-либо событий или их возникновения за одну единицу таймера называется частотой. Это физическая величина измеряется в герцах – Гц (Hz). Она обозначается буквами ν, f, F, и есть отношение количества повторяющихся событий к промежутку времени, в течение которого они произошли.

При обращении предмета вокруг своего центра можно говорить о такой физической величине, как частота вращения, формула:

• N – количество оборотов вокруг оси или по окружности,
• t – время, за которое они были совершены.

В системе СИ обозначается как – с-1 (s-1) и именуется как обороты в секунду (об/с). Применяют и другие единицы вращения. При описании вращения планет вокруг Солнца говорят об оборотах в часах. Юпитер делает одно вращение в 9,92 часа, тогда как Земля и Луна оборачиваются за 24 часа.

Видео:Как определить мощность, частоту вращения, двигателя без бирки или шильдика самому и простоСкачать

Номинальная скорость вращения

Прежде, чем дать определение этому понятию, необходимо определиться, что такое номинальный режим работы какого-либо устройства. Это такой порядок работы устройства, при котором достигаются наибольшая эффективность и надёжность процесса на продолжении длительного времени. Исходя из этого, номинальная скорость вращения – количество оборотов в минуту при работе в номинальном режиме. Время, необходимое для одного оборота, составляет 1/v секунд. Оно называется периодом вращения T. Значит, связь между периодом обращения и частотой имеет вид:

К сведению. Частота вращения вала асинхронного двигателя – 3000 об./мин., это номинальная скорость вращения выходного хвостовика вала при номинальном режиме работы электродвигателя.

Как найти или узнать частоты вращений различных механизмов? Для этого применяется прибор, который называется тахометр.

Видео:Регулирование частоты вращения ротора трехфазных асинхронных двигателейСкачать

Угловая скорость

Когда тело движется по окружности, то не все его точки движутся с одинаковой скоростью относительно оси вращения. Если взять лопасти обычного бытового вентилятора, которые вращаются вокруг вала, то точка расположенная ближе к валу имеет скорость вращения больше, чем отмеченная точка на краю лопасти. Это значит, у них разная линейная скорость вращения. В то же время угловая скорость у всех точек одинаковая.

Угловая скорость представляет собой изменение угла в единицу времени, а не расстояния. Обозначается буквой греческого алфавита – ω и имеет единицу измерения радиан в секунду (рад/с). Иными словами, угловая скорость – это вектор, привязанный к оси обращения предмета.

Формула для вычисления отношения между углом поворота и временным интервалом выглядит так:

• ω – угловая скорость (рад./с);
• ∆ϕ – изменение угла отклонения при повороте (рад.);
• ∆t – время, затраченное на отклонение (с).

Обозначение угловой скорости употребляется при изучении законов вращения. Оно употребляется при описании движения всех вращающихся тел.

Угловая скорость в конкретных случаях

На практике редко работают с величинами угловой скорости. Она нужна при конструкторских разработках вращающихся механизмов: редукторов, коробок передач и прочего.

Вычислить её, применяя формулу, можно. Для этого используют связь угловой скорости и частоты вращения.

• π – число, равное 3,14;
• ν – частота вращения, (об./мин.).

В качестве примера могут быть рассмотрены угловая скорость и частота вращения колёсного диска при движении мотоблока. Часто необходимо уменьшить или увеличить скорость механизма. Для этого применяют устройство в виде редуктора, при помощи которого понижают скорость вращения колёс. При максимальной скорости движения 10 км/ч колесо делает около 60 об./мин. После перевода минут в секунды это значение равно 1 об./с. После подстановки данных в формулу получится результат:

Читайте также: Сальник вторичного вала мазда сх7

К сведению. Снижение угловой скорости часто требуется для того, чтобы увеличить крутящий момент или тяговое усилие механизмов.

Как определить угловую скорость

Принцип определения угловой скорости зависит от того, как происходит движение по окружности. Если равномерно, то употребляется формула:

Если нет, то придётся высчитывать значения мгновенной или средней угловой скорости.

Величина, о которой идёт разговор, векторная, и при определении её направления используют правило Максвелла. В просторечии – правило буравчика. Вектор скорости имеет одинаковое направление с поступательным перемещением винта, имеющего правую резьбу.

Рассмотрим на примере, как определить угловую скорость, зная, что угол поворота диска радиусом 0,5 м меняется по закону ϕ = 6*t:

Вектор ω меняется из-за поворота в пространстве оси вращения и при изменении значения модуля угловой скорости.

Видео:Как определить скорость вращения вала электродвигателя и его мощность.Скачать

Угол поворота и период обращения

Рассмотрим точку А на предмете, вращающимся вокруг своей оси. При обращении за какой-то период времени она изменит своё положение на линии окружности на определённый угол. Это угол поворота. Он измеряется в радианах, потому что за единицу берётся отрезок окружности, равный радиусу. Ещё одна величина измерения угла поворота – градус.

Когда в результате поворота точка А вернётся на своё прежнее место, значит, она совершила полный оборот. Если её движение повторится n-раз, то говорят о некотором количестве оборотов. Исходя из этого, можно рассматривать 1/2, 1/4 оборота и так далее. Яркий практический пример этому – путь, который проделывает фреза при фрезеровании детали, закреплённой в центре шпинделя станка.

Внимание! Угол поворота имеет направление. Оно отрицательное, когда вращение происходит по часовой стрелке и положительное при вращении против движения стрелки.

Если тело равномерно продвигается по окружности, можно говорить о постоянной угловой скорости при перемещении, ω = const.

В этом случае находят применения такие характеристики, как:

• период обращения – T, это время, необходимое для полного оборота точки при круговом движении;
• частота обращения – ν, это полное количество оборотов, которое совершает точка по круговой траектории за единичный временной интервал.

Интересно. По известным данным, Юпитер обращается вокруг Солнца за 12 лет. Когда Земля за это время делает вокруг Солнца почти 12 оборотов. Точное значение периода обращения круглого гиганта – 11,86 земных лет.

Видео:6.2 Кинематический расчет приводаСкачать

Циклическая частота вращения (обращения)

Скалярная величина, измеряющая частоту вращательного движения, называется циклической частотой вращения. Это угловая частота, равная не самому вектору угловой скорости, а его модулю. Ещё её именуют радиальной или круговой частотой.

Циклическая частота вращения – это количество оборотов тела за 2*π секунды.

У электрических двигателей переменного тока это частота асинхронная. У них частота вращения ротора отстаёт от частоты вращения магнитного поля статора. Величина, определяющая это отставание, носит название скольжения – S. В процессе скольжения вал вращается, потому что в роторе возникает электроток. Скольжение допустимо до определённой величины, превышение которой приводит к перегреву асинхронной машины, и её обмотки могут сгореть.

Читайте также: Гост 28300 2010 валы карданные валы

Устройство этого типа двигателей отличается от устройства машин постоянного тока, где токопроводящая рамка вращается в поле постоянных магнитов. Большое количество рамок вместил в себя якорь, множество электромагнитов составили основу статора. В трёхфазных машинах переменного тока всё наоборот.

При работе асинхронного двигателя статор имеет вращающееся магнитное поле. Оно всегда зависит от параметров:

• частоты питающей сети;
• количества пар полюсов.

Скорость вращения ротора состоит в прямом соотношении со скоростью магнитного поля статора. Поле создаётся тремя обмотками, которые расположены под углом 120 градусов относительно друг друга.

Видео:Как посчитать обороты и передаточное число.Скачать

Переход от угловой к линейной скорости

Существует различие между линейной скоростью точки и угловой скоростью. При сравнении величин в выражениях, описывающих правила вращения, можно увидеть общее между этими двумя понятиями. Любая точка В, принадлежащая окружности с радиусом R, совершает путь, равный 2*π*R. При этом она делает один оборот. Учитывая, что время, необходимое для этого, есть период Т, модульное значение линейной скорости точки В находится следующим действием:

Так как ω = 2*π*ν, то получается:

Следовательно, линейная скорость точки В тем больше, чем дальше от центра вращения находится точка.

К сведению. Если рассматривать в качестве такой точки города на широте Санкт-Петербурга, их линейная скорость относительно земной оси равна 233 м/с. Для объектов на экваторе – 465 м/с.

Числовое значение вектора ускорения точки В, движущейся равномерно, выражается через R и угловую скорость, таким образом:

а = ν2/ R, подставляя сюда ν = ω* R, получим: а = ν2/ R = ω2* R.

Это значит, чем больше радиус окружности, по которой движется точка В, тем больше значение её ускорения по модулю. Чем дальше расположена точка твердого тела от оси вращения, тем большее ускорение она имеет.

Поэтому можно вычислять ускорения, модули скоростей необходимых точек тел и их положений в любой момент времени.

Понимание и умение пользоваться расчётами и не путаться в определениях помогут на практике вычислениям линейной и угловой скоростей, а также свободно переходить при расчётах от одной величины к другой.

Видео:Ременная передача. Урок №3Скачать

Видео

Видео:Как за 5 секунд узнать обороты электродвигателя без таблички без разборкиСкачать

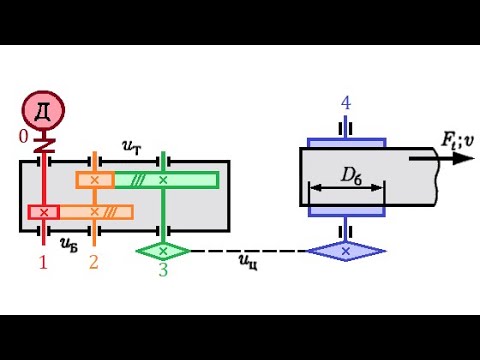
Определение частот вращения и вращающих моментов на валах.

Определение частот вращения на валах.

Определяем общее передаточное число привода:

где

Тогда

Так как , то для расчета передаточного числа зубчатого редуктора примем передаточное число конической передачи равный u_к.п.=4.

Тогда передаточное число зубчатой передачи u_р.п.=2,303

Частоты вращения на валах имеют следующие значения:

Определение вращающих моментов на валах.

Определим момент на валу электродвигателя:

Момент за ременной передачей будет составлять:

Тогда момент на валу за конической передачей будет равна:

Расчет конической передачи

Выбор материала.

По рекомендации произведем выбор для конической передачи материал и вид термической обработки (таблица 2.1 методических указаний).

Второй вариант– колесо – сталь 40Х; твердость поверхности зубьев 269…302НВ; шестерня – сталь 40Х; твердость поверхности зубьев после закалки ТВЧ 45…50 HRC.

Определим среднюю твердость поверхностей зубьев колес и базовые числа нагружений.

Читайте также: Индукционный съемник малой шестерни с вала тягового электродвигателя

По таблице перевода получаем: HB_cp=450

При расчете на изгиб базовое число нагружений принимаем:

Определим действительные числа циклов перемены напряжений:

Рассчитаем время работы передачи:

часов

Общее число циклов перемены напряжения:

Так как N ³ N_HO то K_HL = 1,0

Коэффициент долговечности при расчете на изгиб для всех вариантов термообработки K_FL = 1,0; так как для всех случаев N > 4×10 6 .

Определение допускаемых напряжений.

Допускаемое контактное и изгибающее напряжение напряжение.

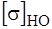
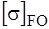
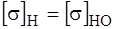
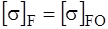
Допускаемые контактные и изгибающие напряжение получаются умножением и на коэффициенты K_HL и K_FL. Так как эти коэффициенты равны 1 то и .

Для второго варианта термообработки допускаемое контактное напряжение, которое должно определятся в расчете:

Проектный расчет.

Предварительно найдем следующие коэффициенты:

u_н = 0,85. Для режима термообработки II коэффициент K_HB = 1

1. Диаметр внешней делительной окружности:

2. Угол делительных конусов колеса и шестерни (2.34):

d₂ = arctgu = arctg4 = 75,964°; sind₂ = cos d₁ =0,97;

b= 0,285 × R_e = 0,285×241,768=68,9» 70 мм.

3. Модуль передачи. Коэффициент K_Fb = 1, так как колеса полностью прирабатываются (II вариант термообработки). Для прямозубых колес коэффициент u_F.=0,85. Допускаемое напряжение изгиба для колеса [s]_F =294 Н/мм 2 (оно меньше, чем для шестерни). После подстановки в формулу (2.37) получаем

4. Число зубьев колеса (2.38)

Число зубьев шестерни (2.39)

5. Фактическое передаточное число

Отклонение от заданного передаточного числа (2.40)

6. Окончательные размеры колес.

Углы делительных конусов колеса и шестерни:

Делительные диаметры колес (2.41):

Внешние диаметры колес (2.43):

7. Пригодность заготовок колес:

Условия пригодности заготовок выполняются (см, табл. 2.1).

Окружная сила на среднем диаметре колеса (2.45)

Осевая сила на шестерне, равная радиальной силе на колесе (2.46),

Радиальная сила на шестерне, равная осевой силе на колесе (2.47),

9. Проверка зубьев колес по напряжениям изгиба.

Предварительно определим значение некоторых коэф­фициентов.

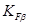
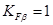
Коэффициент принят равным .

Коэффициент К_FV для прямозубых колес при твердости зубьев колеса

На этом силовой расчет конической передачи заканчи­вается.

Для построения компоновочной схемы нужно дополни­тельно определить некоторые размеры валов. Для вала

колеса (3.1)

Так как опорами вала конического колеса должны быть конические роликовые подшипники, то коэффициент перед корнем следует принять равным 6. Тогда диаметр вала

мм, или, после округления, d=71 мм;

Найдем диаметр d_п: d_п= d + 2×t_цил=71+2×5,1=81,2 мм Выбираем d_п= 85 мм

Произведем расчет диаметра буртика d_БП= d_п + 3×r=85+3×3,5=95,5 мм

Примем стандартное значение d=60 мм;

Принимаем стандартное значение d₂=65:

d_БП= d_п + 3×r=65+3×3,5=75,5 мм

Размеры других участков валов.

Вала колеса с цилиндрическим концом:

Длина посадочного конца вала l_МТ=1,5×d=1,5×71=106,5 мм.

длина промежуточного участка l_КТ=1,2×d_П=1,2×85=102 мм;

длина ступицы колеса l_ст= 1,2×d_K = 1,2×96 ==115,2 мм.

Примем стандартное значение l_ст= 120 мм.

Вала конической шестерни с коническим концом:

Длина посадочного конца вала l_МБ=1,5×d=1,5×60=90 мм.

длина цилиндрического участка 0,15×d = 0,15×60 ==9 мм

длина резьбового участка 0,4×d_П=0,4×65= 26 мм.

диаметр и длина резьбы d_Р=0,9×(d-0,1×l_MБ)= 0,9×(60-0,1×90)=45,9 мм. Принимаем 48 мм

Другие размеры обоих валов выявляются при вычерчива­нии компоновочной схемы.

• Свежие записи
  • Чем отличается двухтактный мотор от четырехтактного
  • Сколько масла заливать в редуктор мотоблока
  • Какие моторы бывают у стиральных машин
  • Какие валы отсутствуют в двухвальной кпп
  • Как снять стопорную шайбу с вала
  • Правообладателям
  • Политика конфиденциальности

  Механика © 2023
  Информация, опубликованная на сайте, носит исключительно ознакомительный характер

  
  

  источники:

  https://evakuatorinfo.ru/chastota-vrascheniya-valov-formula

  🌟 Видео

  Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

  

  Как узнать число пар полюсов и частоту вращения асинхронного трёхфазного двигателя по статору.Скачать

  

  Как регулируется скорость вращения ротора асинхронных электродвигателей.Скачать

  

  Регулирование частоты вращения двигателей постоянного токаСкачать

  

  Как рассчитать диаметр шкивов и линейную скорость?Скачать

  

  Физика.Узнать за 2 минуты.Основные понятия.Что такое частотаСкачать

  

  Неуравновешенность (дисбаланс)ротораСкачать

  

  Ремённые ПередачиСкачать

  

  Урок 87 (осн). Вращательное движение. Период и частота вращенияСкачать

  

  Расчёт диаметров шкивов ремённой передачи. Часть 1. Инструкция на онлайн калькулятор. Тест привода.Скачать

  

  Почему практически невозможно раскрутить двигатель более 20000 оборотов в минуту | B2B На РусскомСкачать

  

  Как увеличить обороты и мощность коллекторного двигателяСкачать

  

  Регулятор частоты вращения часть 1.Скачать