Чему равен момент инерции вала (2 видео)

При выполнении расчетов часто приходится вычислять моменты инерции сложных сечений относительно различных осей, лежащих в плоскости фигуры. Для стандартных поперечных сечений стержней моменты инерции даны в таблицах ГОСТ 8509-93, ГОСТ 8510-86, ГОСТ 57837-2017, ГОСТ 8240-97. В остальных случаях, для выполнения онлайн расчета момента инерции круга, кольца, треугольника, прямоугольного контура, нестандартных сварных швеллера, уголка и двутавра можно воспользоваться данной страницей нашего сайта.

Содержание

Момент инерции треугольника
Момент инерции кольца
Момент инерции прямоугольника
Момент инерции двутавра
Момент инерции уголка
Момент инерции швеллера
Определение моментов инерции
📽️ Видео

Видео:Момент инерцииСкачать

Момент инерции треугольника

МОМЕНТ ИНЕРЦИИ ТРЕУГОЛЬНИКА

Момент инерции треугольника относительно центральной оси, параллельной одной из его сторон вычисляется по формуле:
I_x0 = b×h 3 / 36;
Момент инерции треугольника относительно оси, совпадающей с одной из его сторон:
I_x1 = b×h 3 / 12;
Момент инерции треугольника относительно оси, параллельной одной из его сторон и проходящей через противоположную вершину:
I_x2 = b×h 3 / 4.

Видео:Момент инерции абсолютно твердого тела. 10 класс.Скачать

Момент инерции кольца

Полярный момент инерции Ip, м 4

Момент инерции кольца относительно главной центральной оси:
I_x = π×D 4 /64 — π×d 4 /64;
Полярный момент инерции кольца:
I_p = π×D 4 /32 — π×d 4 /32.

Видео:Расчёт момента инерции тела относительно оси вращения. Момент инерции однородного стержняСкачать

Момент инерции прямоугольника

МОМЕНТ ИНЕРЦИИ ПРЯМОУГОЛЬНИКА

Момент инерции прямоугольника относительно главных центральных осей:
I_x = (b×h 3 — b1×h1 3 )/12;
I_y = (h×b 3 — h1×b1 3 )/12.

Видео:момент инерцииСкачать

Момент инерции двутавра

Моменты инерции двутавра относительно главных центральных осей:
I_x = (B×H 3 — (B — s)×(H — 2t) 3 ) / 12;
I_y = (2t×B 3 + (H — 2t)×s 3 ) / 12.

Видео:Зависимость углового ускорения от момента инерцииСкачать

Момент инерции уголка

Моменты инерции уголка относительно центральных осей:
I_x = (d×(H — y) 3 + B×y 3 — (B — d)×(y — d) 3 ) / 3;
I_y = (d×(B — x) 3 + H×x 3 — (H — d)×(x — d) 3 ) / 3,
где x и y — расстояния от наружных сторон уголка до центральных осей Y и X соответственно.

Видео:Геометрические характеристики. Моменты инерции. Радиусы инерции. Сопромат.Скачать

Момент инерции швеллера

Моменты инерции швеллера относительно главных центральных осей:
I_x = (B×H 3 — (B — s)×(H-2d) 3 ) / 12;
I_y = (H×x 3 — (H — 2d)×(x — s) 3 + d×(B — x) 3 )/3,
где x — расстояния от наружной сторон швеллера до центральной оси Y.

Расчеты моментов инерции по умолчанию выполнены относительно центральных и главных центральных осей сечения. Моменты инерции относительно осей, параллельных главным центральным осям можно вычислить, прибавив к полученному результату произведение квадрата расстояния между соответствующими осями на площадь сечения.

Читайте также: Подшипник вала промежуточного форд эскейп

Видео:5. Момент инерции простейших телСкачать

Определение моментов инерции

Любая электромеханическая система включает, как правило, элементы вращательного и поступательного движения, как правило, от электродвигателя к рабочему органу механизма. Циклы работы электропривода состоит из пуска и разгона системы, установившегося режима, и замедления до полной остановки. Для расчета режимов работы необходимо определить моменты инерции передаточного механизма. Значения моментов инерции простейших геометрических тел приведены ниже. Следует отметить, что момент инерции

, где маховый момент.

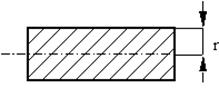
сплошной цилиндр

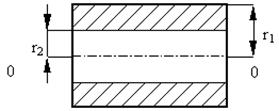
полый цилиндр

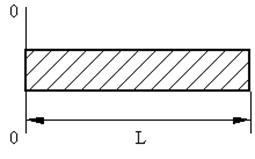
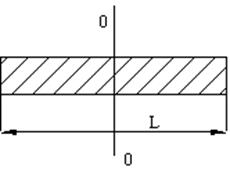
стержень вращается вокруг оси 0_0

Задача 2.1.Компрессор приводится в движение двигателем типа АК-112-8 с номинальными данными: U_ном=380В; Р_ном=160кВт; n_ном=735об/мин. Вал двигателя непосредственно соединен с валом компрессора и маховиком (рисунок 2.1). Момент инерции соединительной муфты и коленчатого вала составляют соответственно 5% и 3% от момента инерции маховика. Материал маховика – чугун с удельным весом γ=7,5 т/м³.Определить момент инерции привода.

1) Определяем массу маховика без пустот

2) Находим возможный момент инерции осевой пустоты

3) Определяем возможный момент инерции полых выемок

Поскольку таких выемок в маховике две, суммарный момент инерции равен .

Задача 2.2. Электродвигатель с маховым моментом GD²=20кг∙м² и маховиком разгоняется до частоты вращения 1500об/мин (рисунок 2.2). Определить момент инерции и время разгона двигателя с пусковым моментом М_п =400Н∙м. Материал маховика – сталь с удельным весом γ=7,8т/м³, решить самостоятельно.

Задача 2.3.Электродвигатель с маховым моментом GD²=10кг∙м² и маховиком разгоняется до частоты вращения 1000об/мин (рисунок 2.3). Определить момент инерции и время разгона двигателя с пусковым моментом М_п =300Н∙м. Материал маховика – сталь с удельным весом γ=7,8т/м³.

Большинство судовых механизмов работают при малых скоростях рабочего органа, тогда как электродвигатели имеют частоту вращения до 3000 об/мин. Поэтому вал электродвигателя соединяется с рабочим органом механизма с помощью редуктора. Для исследования процессов и определения параметров системы её заменяют одним эквивалентным звеном. Такая система называетсяприведенной.Элементы вращательного и поступательного движения приводятся к валу двигателя.

Читайте также: Как открутить гайку шкива коленчатого вала ваз

Задача 2.4.Механизм подъема мостового крана имеет следующие характеристики: Z₁=Z₃=10; Z₂=Z₄=50; n_д=1500об/мин; D_б=0,6м; G=1,5т; GD₀²=1,5 кг∙м²; GD₁²=2 кг∙м²; GD₂²=20 кг∙м² (рисунок 2.4). Определить приведенный к валу двигателя момент инерции, приняв для упрощения к.п.д. равным 100%.

Учитывая, что: определяем

Угловая частота двигателя:

Приведенный момент инерции элементов вращательного движения

Приведенный радиус инерции

Если в реальных условиях принять к.п.д. шестеренок η₁=η₂=0,95 ; барабан-канат η₃=0,95; блок-канат η₄=0,95, тогда будем иметь

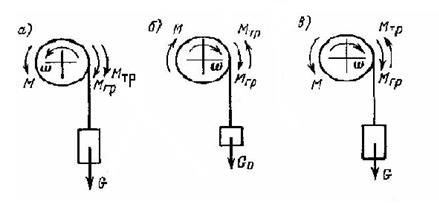
Силы и моменты, действующие

В системе электропривода.

Соотношение статических моментов, преодолеваемых двигателем лебедки при подъеме и спуске одного и того же груза (рис.3.1а).

Рисунок 3.1(а) – Взаимодействие моментов, действующих на вал.

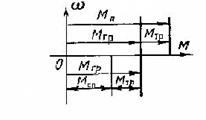
Рисунок 3.1(б) – Абсолютное значение статического момента:

Вычтя из первого уравнения второе, получим (рисунке 3.1.б)

Это соотношение моментов справедливо при расчете грузоподъемных механизмов электроприводов.

Задача 3.2. Определить статические моменты на валу двигателя грузовой трехтонной лебедки при подъеме и спуске номинального груза и холостого гака, если масса холостого гака m₀=60кг; диаметр грузового барабана D_б=400мм; передаточное отношение редуктора i=23,3; КПД механизма при подъеме номинального груза η=0,8.

1.Загрузка механизма при подъеме холостого гака F_x/F_н=m₀/m_н=60/3000=0,02 соответствует КПД (рисунок 3.2) η₀=0,15.

2. Статические моменты (на валу двигателя):

при подъеме номинального груза

при спуске номинального груза

при подъеме холостого гака

при спуске холостого гака

Рисунок 3.2. – Зависимость КПД зубчатых передач η от загрузки механизма

Задача 3.3.Определить время, за которое двигатель лебедки (данные смотри в задаче 3.1.) под действием неизменного пускового момента М_п=450 Н∙м разгонится при подъеме и спуске номинального груза до скорости ω_ст=97 рад/с и остановится после отключения от сети и наложения тормоза с М_т=2М_ст2. Момент инерции двигателя J_дв=1,9 кг∙м². Инерционность передачи и грузового барабана учитываем введением коэффициента k=1,2. Скорость подъема и спуска груза υ=50 м/мин. (В реальных условиях эти скорости определяют из механической характеристики двигателя в соответствии с М_ст.).

Читайте также: В каких втулках вращаются опорные шейки распределительного вала

Решение:Приведенный момент инерции электромеханической системы

источники:

https://evakuatorinfo.ru/chemu-raven-moment-inertsii-vala