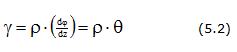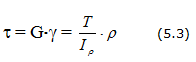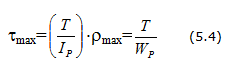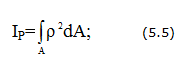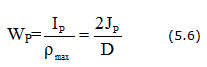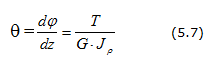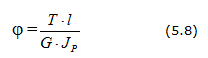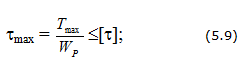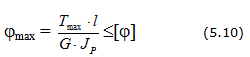Что называется жесткостью вала при кручении

Напряженное состояние, при котором на гранях элемента конструкции возникают только касательные напряжения, называют чистым сдвигом.

Закон Гука при сдвиге имеет вид:

Для изотропных материалов существует зависимость между константами упругости:

Видео:Кручение. Часть 6 Жесткость валаСкачать

Кручение

Кручением называется вид деформации, при котором в любом поперечном сечении бруса возникает только один крутящий момент.

Знак крутящего момента не имеет физического смысла.

Угол закручивания бруса определяется формулой:

Жесткостью сечения при кручении круглого бруса называется величина [GI_p]=H*м 2

Полярным моментом сопротивления сечения кручению называется величина:

Максимальные касательные напряжения достигаются на поверхности круглого бруса и равны:

Опасным сечением при кручении называется поперечное сечение бруса, в котором возникает максимальное касательное напряжение.

Угол закручивания бруса длиной l при постоянном крутящем моменте равен:

Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать

Расчеты на прочность и жесткость при кручении.

1. При проверочном расчете определяется наибольшее касательное напряжение, которое сравнивается с допускаемым касательным напряжением:

2. При проектном расчете определяется площадь и диаметр опасного сечения стержня из условия:

3.При определении допускаемой нагрузки рассчитывается максимальный допускаемый крутящий момент:

1. Условие жесткости при кручении имеет вид:

2.Подбор поперечного сечения бруса осуществляется из условия:

Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

Что называется жесткостью вала при кручении

Элементы конструкции, как уже указывалось, часто схематизируются в виде стержней. Такая модель формы используется и для расчета валов, передающих крутящий момент. Примерами являются валы, приводящие в движение воздушные винты или лопасти вертолета; валы редукторов, станков и т. п.

Работа стержней на кручение встречается во многих других элементах конструкций.

26. Кручение круглых валов

Деформации и напряжения при кручении круглого вала.

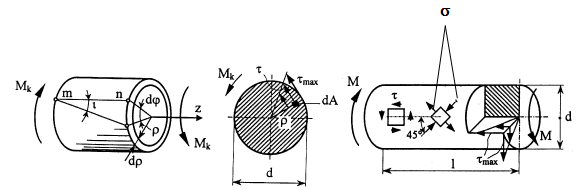
Экспериментально установлено, что при кручении круглого вала (рис. 7.1) приложенным на его торце крутящим моментом поперечные сечения остаются плоскими (рис. 7.2).

Читайте также: 19945 подшипник приводного вала

Рис. 7.1. Кручение круглого вала

Рис. 7.2. Кручение модели вала с предварительно нанесенной сеткой

Можно считать, что поперечные сечения как жесткие круглые диски поворачиваются относительно оси вала на угол .

Образующие, расположенные на цилиндрической поверхности радиусом , поворачиваются на угол постоянный по длине цилиндра (вала). Для малых углов

где — угол закрутки на единицу длины вала; при измерении угла в радианах угол измеряется в единицах . Угол поворота в сечении

Из последнего соотношения можно установить, что

Рассмотрим перемещения и деформации в произвольной точке поперечного сечения А, лежащей на расстоянии от оси вала (рис. 7.3). Перемещение точки равно и направлено перпендикулярно радиусу. В кольцевом слое толщиной возникает деформация сдвига (рис. 7.4)

По закону упругости углу сдвига соответствует касательное напряжение (разд. 18)

где G — модуль сдвига,

Учитывая (4), находим важную зависимость:

Касательное напряжение направлено по касательной к окружности радиусом . Величина касательного напряжения пропорциональна радиусу (рис. 7.5).

Рис. 7.3. Картина перемещений точек вала при кручении

Рис. 7.4 Деформация сдвига в кольцевом слое

Рис. 7.5. Распределение касательных напряжений при кручении

Из общих условий равновесия следует, что касательные усилия должны создавать крутящий момент

где — полярный момент инерции сечения вала. Величину полярного момента легко вычислить, приняв

Из соотношения (6) получаем формулу для относительного угла закрутки

Величина называется жесткостью (сечения) вала на кручение. Угол поворота сечения вала

Взаимпый поворот сечений на участке вала длиной I

Внося значение в формулу (5), находим важную расчетную зависимость:

Наибольшее касательное напряжение получается на внешнем радиусе

называется моментом сопротивления кручению; таким образом,

Анализ решения методами теории упругости.

Полученное решение о распределении напряжений и деформаций при кручении вала основывалось на экспериментальных наблюдениях. Попробуем подвергнуть его анализу с позиции общих уравнении механики деформируемого тела. В соответствии с принятой моделью деформации вала перемещение точки , равное (рис. 7.6), имеет составляющие по осям

Читайте также: Подшипник промежуточного вала газель некст нового образца задний

Рис. 7.6. Кручение круглого вала. Расчет методом теории упругости

Перемещение вдоль оси z отсутствует . Составляющие касательного напряжения равны

Полное касательное напряжение

что совпадает с равенством (5). Можно показать, что при удовлетворяются уравнения равновесия и краевые условия на боковых поверхностях вала. Принятую модель деформации круглого вала следует признать точной.

Замечания. 1. Предполагается, что в концевых сечениях вала внешний крутящий момент реализуется в виде линейно распределенных касательных напряжений (см. рис. 7.5). В действительности момент обычно прикладывается по-другому (например, с помощью шлицевого соединения (рис. 7.7)), и поэтому по принципу Сен-Венана решение будет справедливым на некотором удалении от торцов.

Рис. 7.7. Передача крутящего момента на вал с помощью шлицевого соединения

Более строго следовало бы сказать, что решение является точным для неконцевых областей вала.

2. Граница между понятиями «точного» и «приближенного» решения в применении к практическим задачам часто носит условный характер. Например, можно получить точное решение для весьма приближенной модели (расчетной схемы) или приближенное решение для более точной модели. Что лучше для практических, целей? Однозначного ответа на этот вопрос не существует.

На основании практического опыта вырабатываются модели различных уровней, используемые на разных этапах проектирования (предварительный выбор размеров на стадии технического предложения, более точные модели на этапах эскизного и рабочего проектирования).

Видео:Сопротивление материалов. Лекция: расчёт на прочность при крученииСкачать

iSopromat.ru

Для обеспечения прочности и жесткости вала при кручении, напряжения и деформации от крутящих моментов не должны превышать соответствующих допустимых значений.

Этот вид нагружения возникает при приложении к брусу пар сил, плоскости действия которых перпендикулярны его оси. Такие брусья принято называть валами.

Внешние пары, приложенные к валу, будем называть скручивающими моментами. Они могут быть сосредоточенными М₁, М₂, …, М_n или распределенными m по длине вала l .

Читайте также: Течет задний сальник коленчатого вала

Крутящий момент является равнодействующим моментом напряжений, возникающих в каком-либо сечении вала относительно его продольной оси.

Видео:Сопромат. Практическое занятие №1.4Скачать

Внутренний крутящий момент

При определении величины крутящего момента используется метод сечений. Суть его заключается в следующем: рассекаем вал сечением и отбрасываем одну из частей вала, расположенную либо справа, либо слева от сечения.

Обычно отбрасывают ту часть, к которой приложено больше скручивающих пар. Действие отброшенной части на рассматриваемую заменяют внутренним силовым фактором – крутящим моментом T . Затем из условий равновесия остановленной части вала определяют крутящий момент:

Таким образом, крутящий момент в каком либо сечении вала является уравновешивающей парой сил всех внешних скручивающих пар, приложенных либо слева, либо справа от рассматриваемого сечения.

Видео:Кручение валаСкачать

Напряжения при кручении

Распределение касательных напряжений

Максимальное касательное напряжение

Геометрические характеристики круглых сплошных сечений вала

Полярный момент сопротивления

Видео:Сопромат. Построение эпюр вала при кручении. Я в вк https://vk.com/id4682924Скачать

Деформации вала

Видео:Правило знаков при крученииСкачать

Условия прочности и жесткости вала

Расчет вала при кручении сводится к одновременному удовлетворению двух условий:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:12. Подбор сечения при кручении ( практический курс по сопромату )Скачать

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

Видео:Прочность и жесткость валов. Часть 6: Эпюры моментов выходного вала (цилиндрическая передача).Скачать

Набор студента для учёбы

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

• Свежие записи
  • Чем отличается двухтактный мотор от четырехтактного
  • Сколько масла заливать в редуктор мотоблока
  • Какие моторы бывают у стиральных машин
  • Какие валы отсутствуют в двухвальной кпп
  • Как снять стопорную шайбу с вала
  • Правообладателям
  • Политика конфиденциальности

  Механика © 2023
  Информация, опубликованная на сайте, носит исключительно ознакомительный характер

  
  

  источники:

  https://evakuatorinfo.ru/chto-nazyvaetsya-zhestkostyu-vala-pri-kruchenii

  🎬 Видео

  11. Кручение ( практический курс по сопромату )Скачать

  

  9.1 Расчет валов приводаСкачать

  

  Кручение. Часть 1 Общие сведенияСкачать

  

  КРУЧЕНИЕ. ЭПЮРЫ ЗАКРУЧИВАНИЯ. Углы поворота. СопроматСкачать

  

  Деформации и перемещения. Расчет на жесткостьСкачать

  

  Изгиб с кручениемСкачать

  

  Сопротивление материалов. Лекция: кручение круглого стержняСкачать

  

  Понимание напряжений в балкахСкачать

  

  Неуравновешенность (дисбаланс)ротораСкачать

  

  Видеоурок 6. Расчеты на прочность и жесткость при изгибе.Скачать