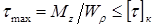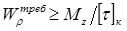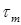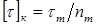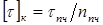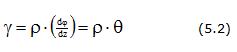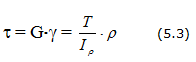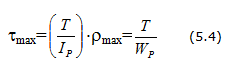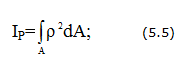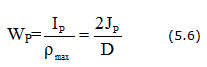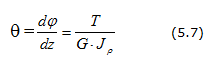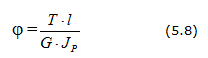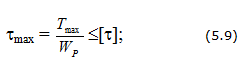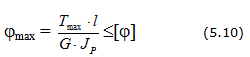Что определяется из условия прочности вала при кручении

Условие прочности при кручении: прочность вала считается обеспеченной, если наибольшие касательные напряжения, возникающие в его опасном поперечном сечении, не превышают допускаемых напряжений на кручение :

Формула служит для проверочного расчета вала на прочность.

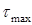
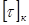
Допускается незначительное (до 5 %) превышение расчетного напряжения над допускаемым напряжением .

При проектировочном расчете требуемый полярный момент сопротивления определяется по формуле условия прочности при кручении :

.

Для вала постоянного диаметра опасным сечением при кручении является сечение, в котором возникает наибольший крутящий момент. Если сечение вала не постоянно по длине, может оказаться, что наибольшие касательные напряжения возникают не там, где крутящий момент максимален. Следовательно, в этом случае вопрос об опасном сечении должен быть исследован дополнительно.

Допускаемое напряжение :

для пластичных материалов назначается в зависимости от предела текучести () при кручении (сдвиге):

.

для хрупких материалов назначается в зависимости от предела прочности:

.

Видео:Сопромат. Практическое занятие №1.4Скачать

iSopromat.ru

Для обеспечения прочности и жесткости вала при кручении, напряжения и деформации от крутящих моментов не должны превышать соответствующих допустимых значений.

Этот вид нагружения возникает при приложении к брусу пар сил, плоскости действия которых перпендикулярны его оси. Такие брусья принято называть валами.

Внешние пары, приложенные к валу, будем называть скручивающими моментами. Они могут быть сосредоточенными М₁, М₂, …, М_n или распределенными m по длине вала l .

Крутящий момент является равнодействующим моментом напряжений, возникающих в каком-либо сечении вала относительно его продольной оси.

Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать

Внутренний крутящий момент

При определении величины крутящего момента используется метод сечений. Суть его заключается в следующем: рассекаем вал сечением и отбрасываем одну из частей вала, расположенную либо справа, либо слева от сечения.

Обычно отбрасывают ту часть, к которой приложено больше скручивающих пар. Действие отброшенной части на рассматриваемую заменяют внутренним силовым фактором – крутящим моментом T . Затем из условий равновесия остановленной части вала определяют крутящий момент:

Таким образом, крутящий момент в каком либо сечении вала является уравновешивающей парой сил всех внешних скручивающих пар, приложенных либо слева, либо справа от рассматриваемого сечения.

Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

Напряжения при кручении

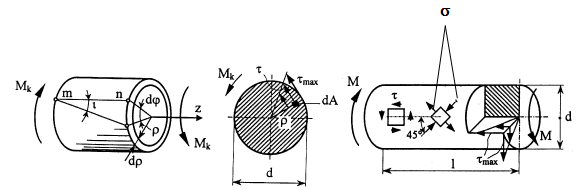
Распределение касательных напряжений

Максимальное касательное напряжение

Геометрические характеристики круглых сплошных сечений вала

Полярный момент сопротивления

Видео:Сопротивление материалов. Лекция: расчёт на прочность при крученииСкачать

Деформации вала

Видео:Правило знаков при крученииСкачать

Условия прочности и жесткости вала

Расчет вала при кручении сводится к одновременному удовлетворению двух условий:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Читайте также: Если не работает компрессор в морозильной камере

Видео:12. Подбор сечения при кручении ( практический курс по сопромату )Скачать

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

Видео:11. Кручение ( практический курс по сопромату )Скачать

Набор студента для учёбы

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Видео:Кручение. Часть 6 Жесткость валаСкачать

Условие прочности при кручении

Условие прочности при кручении: прочность вала считается обеспеченной, если наибольшие касательные напряжения, возникающие в его опасном поперечном сечении, не превышают допускаемых напряжений на кручение:

Формула служит для проверочного расчета вала на прочность.

Допускается незначительное (до 5 %) превышение расчетного напряжения 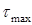над допускаемым напряжением .

При проектировочном расчете требуемый полярный момент сопротивления определяется по формуле условия прочности при кручении:

.

Для вала постоянного диаметра опасным сечением при кручении является сечение, в котором возникает наибольший крутящий момент. Если сечение вала не постоянно по длине, может оказаться, что наибольшие касательные напряжения возникают не там, где крутящий момент максимален. Следовательно, в этом случае вопрос об опасном сечении должен быть исследован дополнительно.

Допускаемое напряжение :

для пластичных материалов назначается в зависимости от предела текучести ( ) при кручении (сдвиге):

.

для хрупких материалов назначается в зависимости от предела прочности:

.

Условие жесткости при кручении

За меру жесткости при кручении принимается относительный угол закручивания вала ( ). Формула условия жесткости при кручении:

,

где – значение допускаемого относительного угла закручивания, град/м, зависящее от назначения вала

Пример решения задачи на кручение стержня круглого сечения

Условие задачи

К стальному валу постоянного поперечного сечения (рис. 3.8) приложены четыре внешних скручивающих момента: кН·м; кН·м; кН·м; кН·м. Длины участков стержня: м; м, м, м. Требуется: построить эпюру крутящих моментов, определить диаметр вала при кН/см2 и построить эпюру углов закручивания поперечных сечений стержня.

Кручение стержня круглого сечения – расчетная схема

Решение задачи кручение стержня круглого сечения

Видео:Изгиб с кручениемСкачать

Тема 2.4. Кручение

Под кручением понимается такой вид деформации, когда в поперечных сечениях бруса действует только крутящий момент M_k, (другое обозначение T, M_z), а остальные силовые факторы (нормальная и поперечная силы и изгибающие моменты) отсутствуют.

Или другое определение кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рис.1).

Кручение возникает в валах, винтовых пружинах, в элементах пространственных конструкций и т.п.

Деформация кручения наблюдается если прямой брус нагружен внешними моментами (парами сил M), плоскости действия которых перпендикулярны к его продольной оси

Читайте также: Что нужно для ремонта карданных валов

В чистом виде деформация кручения встречается редко, обычно присутствуют и другие внутренние силовые факторы (изгибающие моменты, продольные силы).

Стержни круглого или кольцевого сечения, работающие на кручение, называют валами.

Внешние крутящие моменты передаются на вал в местах посадки на него шкивов, зубчатых колес, там, где поперечная нагрузка смещена относительно оси вала.

Мы будем рассматривать прямой брус только в состоянии покоя или равномерного вращения. В этом случае алгебраическая сумма всех внешних скручивающих моментов, приложенных к брусу, будет равна нулю.

При расчете брусьев, испытывающий деформацию кручения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от M_k), возникающих в брусе, и нахождение угловых перемещений в зависимости от внешних скручивающих моментов.

При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.

В ряде случаев величины внешних крутящих моментов определяются по величине потребляемой мощности и по скорости вращения вала. Если вал делает в минуту n оборотов (n- частота вращения, единицы измерения — об/мин.), то вращающий момент можно найти по формуле: М_вр=P/n,

эта формула дает значение момента в Н·м, если мощность выражена в Вт, а частота вращения n — об/мин.

§2. Построение эпюр крутящих моментов

Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов M_k (M_z) в поперечных сечениях по длине вала. Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.

В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣM_z=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 1, крутящий момент M_z в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M₁|=|M₂|.

Видео:КРУЧЕНИЕ. ЭПЮРЫ ЗАКРУЧИВАНИЯ. Углы поворота. СопроматСкачать

Расчет валов на прочность и жесткость при кручении

Видео:Вал. Расчет на прочность при косом изгибе и крученииСкачать

Расчет валов на прочность и жесткость при кручении

• Расчет вала на прочность И жесткость на кручение Для своей конструкции можно рекомендовать следующий порядок расчета вала на прочность и жесткость при кручении. По схеме вала и действующему на него крутящему моменту строится график

Читайте также: Подшипники вала измельчителя акрос

крутящего момента для отдельных участков (§ 16). Выберите материал расчетного вала и определите допустимое напряжение[t] для этого материала. Условия записи Секционная прочность 214 вала с максимальным значением крутящего момента(согласно диаграмме крутящего момента) (9.12).

Если вал достаточно длинный и отдельные секции достаточно сильно отличаются по величине крутящего Людмила Фирмаль

момента, то они должны быть ступенчато спроектированы. Диаметр вала каждой ступени рассчитывается по одной и той же формуле(9.12), но значения крутящего момента различны для разных участков в зависимости от графика крутящего момента. Учитывая, что можно написать формулу для расчета диаметра вала

из сплошного круглого вала Wp=уравнение (9.13: (9.16) Определить диаметр полой оси, заданный соотношением между размерами внутреннего и наружного диаметров из конструктивных соображений, т. е. коэффициент= — тогда, учитывая уравнение(9.11), из уравнения (9.13)следует:: (9.17)) После определения размеров вала из условий прочности проверьте жесткость вала по формуле (9.14).

• Допустимый относительный угол поворота вала составляет 0,3°для каждого метра статической нагрузки[0′] — длина вала, переменная нагрузка[0°1=0,25°, ударная нагрузка[0 ′ 4=0,15°]. Учитывая, что формула (9.14) представляет угол закрутки в радианах, значение данного допустимого угла преобразуется в радианы, и в испытании выполняется условие жесткости (9.14), в противном случае размеры вала должны выбираться из условия жесткости(9.15).): Подставляя в эту формулу формулу момента полярной инерции, находим ее для непрерывной оси (9.18) Для полого вала Иногда при расчете вала

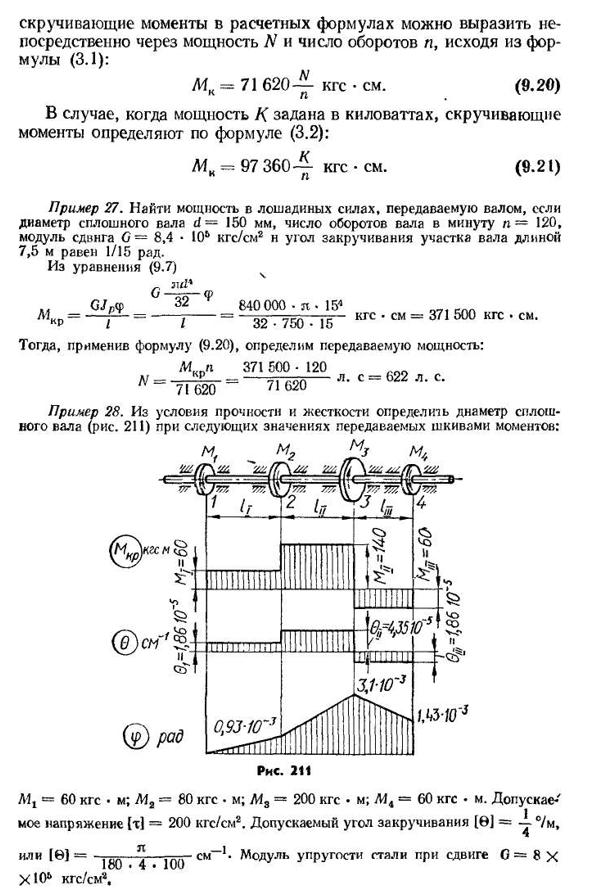
известно, что передаваемая мощность n равна лошадиным силам, а число оборотов-n в минуту. В этом деле 21 крутящий момент формулы может быть выражен непосредственно в терминах мощности n и числа оборотов n, исходя из Формулы (3.1): МК=71 620-кгс*(9.20) мощность/(задается в киловаттах, когда крутящий момент определяется по формуле (3.2): МК-97 360-кгс * см.(9.21）) >

27, например. Найти мощность, передаваемую валом, диаметр Людмила Фирмаль

сплошного вала d-150мм, число оборотов вала n-120 в минуту, модуль сдвига G— 8,4 • 10 длина участка оси кгс / см2н с углом кручения 7,5 м составляет 1/15 Радиана. Из уравнения(9.7) И ой.. GJpat/7=/7 / =50 см h=J=90 см. В этом случае одна из секций фиксируется (рис. 211 настоящего раздела/). В пределах каждой секции 0-const угол кручения каждой секции изменяется по линейному закону,B, MD. Max=M V и формула на основе L\ymk В (А+Б) л[т] *

• Свежие записи
  • Чем отличается двухтактный мотор от четырехтактного
  • Сколько масла заливать в редуктор мотоблока
  • Какие моторы бывают у стиральных машин
  • Какие валы отсутствуют в двухвальной кпп
  • Как снять стопорную шайбу с вала

  
  

  источники:

  https://evakuatorinfo.ru/chto-opredelyaetsya-iz-usloviya-prochnosti-vala-pri-kruchenii

  🎦 Видео

  9.1 Расчет валов приводаСкачать

  

  Кручение валаСкачать

  

  Расчет вала на изгиб с кручениемСкачать

  

  Сопротивление материалов. Занятие 7. Расчет на прочность. Кручение стержняСкачать

  

  Статически неопределимый вал. Расчет на прочность при крученииСкачать

  

  Сопротивление материалов. Лекция: кручение круглого стержняСкачать

  

  Изгиб с кручением пример решения задач по сопротивлению материалов. Теории прочностиСкачать

  

  Видеоурок 6. Расчеты на прочность и жесткость при изгибе.Скачать

  

  Прочность и жесткость валов. Часть 6: Эпюры моментов выходного вала (цилиндрическая передача).Скачать