Что такое кручение валов

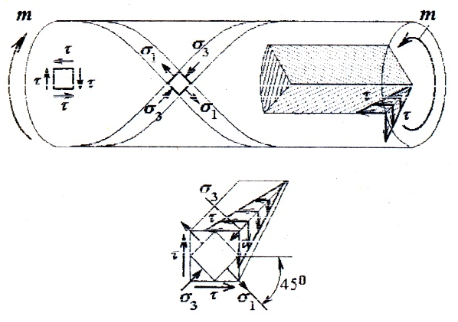
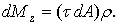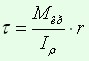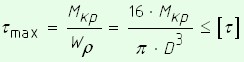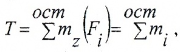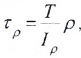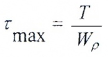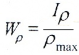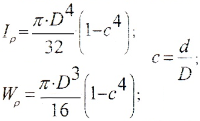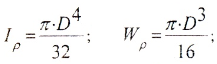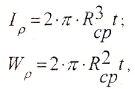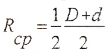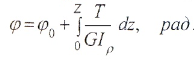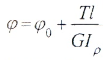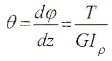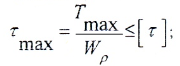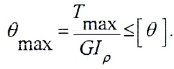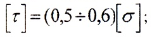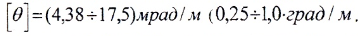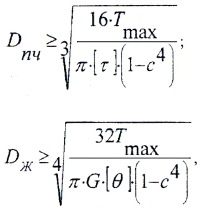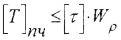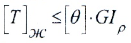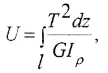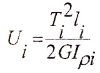Напряженное состояние, при котором на гранях элемента конструкции возникают только касательные напряжения, называют чистым сдвигом.

Закон Гука при сдвиге имеет вид:

Для изотропных материалов существует зависимость между константами упругости:

Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

Кручение

Кручением называется вид деформации, при котором в любом поперечном сечении бруса возникает только один крутящий момент.

Знак крутящего момента не имеет физического смысла.

Угол закручивания бруса определяется формулой:

Жесткостью сечения при кручении круглого бруса называется величина [GI_p]=H*м 2

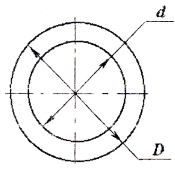
Полярным моментом сопротивления сечения кручению называется величина:

Максимальные касательные напряжения достигаются на поверхности круглого бруса и равны:

Опасным сечением при кручении называется поперечное сечение бруса, в котором возникает максимальное касательное напряжение.

Угол закручивания бруса длиной l при постоянном крутящем моменте равен:

Видео:Кручение. Часть 1 Общие сведенияСкачать

Расчеты на прочность и жесткость при кручении.

1. При проверочном расчете определяется наибольшее касательное напряжение, которое сравнивается с допускаемым касательным напряжением:

2. При проектном расчете определяется площадь и диаметр опасного сечения стержня из условия:

3.При определении допускаемой нагрузки рассчитывается максимальный допускаемый крутящий момент:

1. Условие жесткости при кручении имеет вид:

2.Подбор поперечного сечения бруса осуществляется из условия:

Видео:11. Кручение ( практический курс по сопромату )Скачать

Кручение

Кручение — это такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор — крутящий момент М .

Деформация кручения возникает при нагрузке стержня парами сил, плоскости действия которых перпендикулярны к его продольной оси.

На рис. а изображен брус, работающий на кручение под действием приложенных к нему крутящих моментов. Это условное изображение моментов равнозначно показанном на рис. б .

Обозначения крутящих моментов

• соблюдается гипотеза плоских сечений;
• сечения при кручении не деформируются;
• расстояния между поперечными сечениями не изменяются;
• ось стержня остается прямой (не сгибается);
• деформация кручения вала эт ’ связана с деформацией сдвига.

Применяя метод сечений и рассматривая равновесие отсеченной части, приходим к выводу, что внутренние силы, возникающие в поперечном сечении бруса, должны приводиться к крутящего момента, что уравновешивает внешние моменты, приложенные к отсеченной части.

Итак, крутящий момент, возникающий в произвольном поперечном сечении бруса численно равен алгебраической сумме крутящих моментов, приложенных к отсеченной части .

Представление о характере деформации можно получить, подвергая скручиванию резиновую модель бруса с нанесенной на ее поверхности сеткой продольных и поперечных рисок (рис а). Поперечные черточки не искривляются, и расстояния между ними не изменяются, что можно рассматривать как подтверждение первого и второго допущений. Продольные риски обращаются в винтовые линии (рис. б).

Читайте также: Очистка вала заряда kyocera

Справедливость принятых допущений подтверждается, кроме того, и тем, что полученные на основе их формулы совпадают с формулами, полученными в теории упругости без этих допущений, хорошо согласуются с экспериментальными данными.

Рассмотрим брус, жестко защемленный одним концом и нагруженный на свободном конце крутящим моментом . При деформации бруса его поперечные сечения повернутся на некоторые углы относительно своего первоначального положения.

Угол поворота будет тем больше, чем дальше отстоит данный сечения от заделки. Так, для произвольного сечения I , что отстоит от заделки на расстояние , она равна , а для сечения II — . Здесь — угол поворота сечения II относительно I , или угол закручивания элемента бруса длиной .

Вообще угол поворота произвольного сечения равен углу закручивания части бруса, заключенной между этим сечением и заделкой. Таким образом, угол поворота торцевого сечения представляет собой полный угол закручивания рассматриваемого бруса.

Применяя метод сечений, легко убедиться, что крутящий момент во всех поперечных сечениях бруса одинаков: . Выразим его через касательные напряжения, возникающие в поперечном сечении. При этом учтем, что в любой точке поперечного сечения касательное напряжение направлено перпендикулярно к радиусу, проведенному в эту точку (рис. 14.4).

Такое направление напряжений следует из характера деформации: при повороте произвольного поперечного сечения каждая его точка (кроме лежащей на оси бруса) перемещается по дуге окружности, концентричной контура сечения. Другими словами, направление этого перемещения, а значит и возникающего в этой точке касательных напряжений, перпендикулярно соответствующему радиусу.

Направление перемещения и касательных напряжений

Элементарная касательная сила, приходящаяся на площадку , равна , а ее момент относительно оси (точки В ):

Суммируя эти элементарные моменты, получаем следующее выражение для крутящего момента:

Хотя крутящий момент может рассматриваться как известная величина (определяется с помощью метода сечений через заданные внешние моменты), использовать выражение для вычисления касательных напряжений невозможно, потому что закон их распределения по поперечному сечении пока неизвестен. Для выяснения этого закона рассмотрим более подробно вопрос о деформации.

Выделим часть бруса двумя бесконечно близкими поперечными сечениями. Будем считать выделенную часть бруса затиснену в сечении I (рис.15.5), что вполне допустимо, потому что нас интересуют ее деформации, а не перемещение в пространстве как твердого тела. Точка В , взята на контуре сечения II , в результате его поворота на угол перейдет в положение Деформация сдвига соответствующего элемента бруса (торец этого элемента, что лежит в сечении II , зачернений) характеризуется углом сдвига Из прямоугольного треугольника , ввиду того, что , и в силу малости деформаций получаем

Читайте также: Валы конструктивные элементы материалы

Выделяя мысленно из рассматриваемой части бруса цилиндр произвольного радиуса, и повторяя те же рассуждения, есть

Применяя закон Гука для сдвига $\left( \right)$, получаем следующее выражение для касательных напряжений

Подставляя (7.6) в (7.4), получаем

При интегрировании по площади поперечного сечения величина постоянная и, так же как и G , может быть вынесена за знак интеграла:

Интеграл, входящий в выражение , представляет собой полярный момент инерции сечения (см. раздел 2), следовательно,

.

.

Формула позволяет определить величину касательных напряжений в любой точке поперечного сечения. Из этой формулы следует, что касательные напряжения распределены вдоль любого радиуса сечения по линейному закону.

Эпюры касательных напряжений для круглых сплошных и кольцевого поперечных сечений показаны на рис. 15.6.

Распределение касательных напряжений при кручении

В точках, равноудаленных от центра сечения, напряжения одинаковые. Наибольшего значения касательные напряжения достигают в точках контура поперечного сечения. Они могут быть определены путем подстановки в (7.9) вместо его наибольшего значения, то есть :

.

Величина $\frac >> = $ представляет собой полярный момент сопротивления, следовательно, получим следующее выражение для максимального касательных напряжений:

.

Условие прочности при кручении сплошного круглого вала будет иметь вид

.

Формулу для углов закручивания получим, интегрируя:

В частном случае, если диаметр бруса постоянный и крутящий момент во всех сечениях одинаковое значение,

В случае постоянства крутящего момента лишь в пределах отдельных участков бруса или ступенчатой изменения его поперечного сечения формулу (7.13) можно применять только по участкам.

Произведение $G \cdot $ называют жесткостью сечения круглого бруса при кручении. Модуль сдвига характеризует свойства материала, а полярный момент инерции является геометрической характеристикой бруса.

Видео:Кручение валаСкачать

iSopromat.ru

Кручением называется такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент T.

Брусья, испытывающие кручение, принято называть валами.

Видео:ИЗМЕРЯЙ ОБОРОТЫ ВАЛА,ТЕЛЕФОНОМ# ЛАЙФХАК,КАК ИЗМЕРИТЬ ОБОРОТЫ ДВИГАТЕЛЯ# ВЕРСИЯ 2Скачать

Внутренний крутящий момент

Внутренние скручивающие моменты появляются под действием внешних крутящих моментов m_i, расположенных в плоскостях, перпендикулярных к продольной оси бруса.

Скручивающие моменты передаются на вал в местах посадки зубчатых колес, шкивов ременных передач и т.п.

Величина крутящего момента в любом сечении вала определяется методом сечений:

т.е. крутящий момент численно равен алгебраической сумме скручивающих моментов m_i, расположенных по одну сторону от рассматриваемого сечения.

Правило знаков внутренних скручивающих моментов:
Положительными принимаются внутренние моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки, при рассмотрении со стороны отброшенной части вала.

В технике наиболее широко используются валы круглого поперечного сечения.

Читайте также: Как определить частоту вращения вала формула

Теория кручения круглых валов основана на следующих гипотезах:

1. поперечное сечение, плоское до деформации вала, остается плоским и после деформации;
2. радиусы, проведенные мысленно в любом поперечном сечении, в процессе деформации вала не искривляются.

Видео:Кручение. Часть 6 Жесткость валаСкачать

Напряжения при кручении

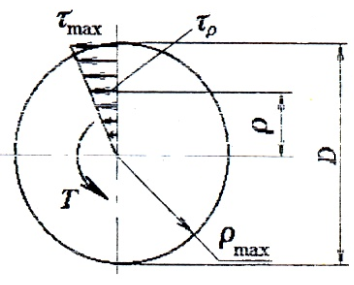
В поперечных сечениях вала при кручении имеют место только касательные напряжения.
Касательные напряжения, направленные перпендикулярно к радиусам, для произвольной точки, отстоящей на расстоянии ρ от центра, вычисляются по формуле:

где I_ρ — полярный момент инерции.
Эпюра касательных напряжений при кручении имеет следующий вид:

Касательные напряжения меняются по линейному закону и достигают максимального значения на контуре сечения при ρ= ρ_max:

Здесь:

— полярный момент сопротивления.
Геометрические характеристики сечений:
а) для полого вала:


б) для вала сплошного сечения (c=0)

в) для тонкостенной трубы (t 0,9)

где

— радиус срединной поверхности трубы.

Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать

Деформации

Деформации валов при кручении заключаются в повороте одного сечения относительно другого.

Угол закручивания вала на длине Z определяется по формуле:

Если крутящий момент и величина GI_ρ, называемая жесткостью поперечного сечения при кручении, постоянны, для участка вала длиной l имеем:

Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания:

Расчет валов сводится к одновременному выполнению двух условий:

1. условию прочности:
   
2. условию жесткости:
   

Для стальных валов принимается:

• допускаемое касательное напряжение
  
• допускаемый относительный угол закручивания
  

Используя условия прочности и жесткости, как и при растяжении – сжатии можно решать три типа задач:

1. проверочный расчет, заключающийся в проверке выполнения условий прочности и жесткости при известных значениях крутящего момента, размеров и материала вала.
2. Проектировочный расчет, при котором вычисляются диаметры:
   
   при этом берется большее из найденных значений, а затем принимается стандартное значение по ГОСТ.
3. Определение грузоподъемности вала:
   • из условия прочности
     
   • из условия жесткости
     

При кручении, наряду с касательными напряжениями в поперечных сечениях, в соответствии с законом парности, касательные напряжения возникают и в продольных сечениях. Таким образом, во всех точках вала имеет место чистый сдвиг.

Главные напряжения σ₁ = τ, σ₃ = -τ наклонены под углом α=±45 о к образующей.

Потенциальная энергия упругой деформации определяется по формуле

или для участка вала при постоянном T и GI_ρ

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

• Свежие записи
  • Чем отличается двухтактный мотор от четырехтактного
  • Сколько масла заливать в редуктор мотоблока
  • Какие моторы бывают у стиральных машин
  • Какие валы отсутствуют в двухвальной кпп
  • Как снять стопорную шайбу с вала

  
  

  источники:

  https://evakuatorinfo.ru/chto-takoe-kruchenie-valov

  💡 Видео

  Строение и функция коленчатого вала (3D анимация) - Motorservice GroupСкачать

  

  Как определить скорость вращения вала электродвигателя и его мощность.Скачать

  

  Основы работы в среде Solidworks Simulation. Кручение цилиндрического валаСкачать

  

  Как определить мощность, частоту вращения, двигателя без бирки или шильдика самому и простоСкачать

  

  Кручение зажатого валаСкачать

  

  Полный курс пдд 2024 Вебинар №36 Устройство АвтоСкачать

  

  Как определить вращение насоса НШ /3 способа/Скачать

  

  Изгиб с кручениемСкачать

  

  Замена датчика частоты вращения входного вала АКПП FN4A-EL на Mazda Demio. Ошибка P0715Скачать

  

  Максимальная частота вращения вала двигателя 4000 об/минСкачать

  

  Ременная передача. Урок №3Скачать

  

  Двигатель от старой стиральной машины. Меняем направление вращения вала.Скачать

  

  Сопротивление материалов. Лекция: кручение круглого стержняСкачать