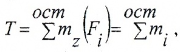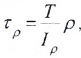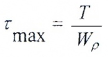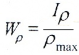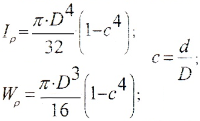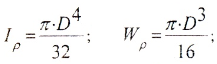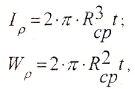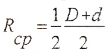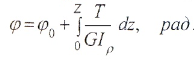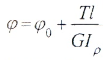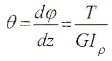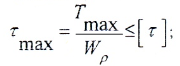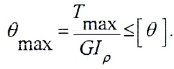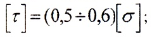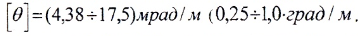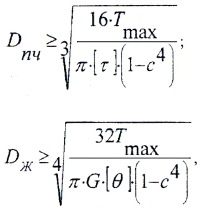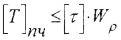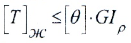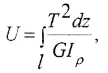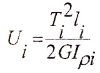Что такое напряжение в поперечных сечениях вала

Кручение прямого стержня в простейшем случае будет происходить, например, от двух пар сил, приложенных к его концевым поперечным сечениям и действующих в их плоскостях, моменты которых равны по величине и противоположны по направлению (рис. 1, а). Моменты внешних паp, вызывающих кручение, называют скручивающими моментами. На практике наиболее часто встречается кручение прямых стержней круглого поперечного сечения, которые называют валами.

Чтобы определить внутренние усилия в каком-либо по­перечном сечении вала, используем метод сечений. Для этого плоскостью А, перпендикулярной к оси вала, мыслен­но рассекаем его на две части — левую и правую. Затем также мысленно отбрасываем одну из них, например, пра­вую, а ее действие на оставшуюся левую заменяем внут­ренними усилиями, которые должны уравновесить внешний скручивающий момент М, поскольку вал в целом находится в состоянии равновесия. Очевидно, что для такого урав­новешивания к поперечному сечению необходимо приложить только один крутящий момент М_к (рис. 1, б).

Таким образом, при кручении в поперечных сечениях вала возникают только крутящие моменты

Из уравнения равновесия для левой рассматриваемой части вала ΣМ_х=0 крутящий момент будет

В общем случае на рассматриваемую часть вала может действовать несколько скручивающих моментов. Тогда из того же уравнения равновесия

т. е. крутящий момент в каком-либо поперечном сечении вала при его кручении численно равен алгебраической сум­ме всех скручивающих моментов, действующих только на рассматриваемую часть вала (рассматривают или левую или правую часть вала). При этом крутящий момент принимают положительным от внешнего момента, вызывающего закручивание рассматриваемой части вала в районе взятого сечения по часовой стрелке, если смотреть на нее со сторо­ны сечения, и отрицательным от внешнего момента, вызы­вающего закручивание против часовой стрелки.

Эпюра крутящих моментов

Эпюра крутящих моментов – это графическое изображение закона распределения крутящих моментов по длине вала. Ординаты эпюры М_к в принятом масштабе выражают величины крутящих моментов в соответствующих поперечных сечениях вала.

При построении эпюры вал разбивают на отдельные участки, в пределах которых крутящие моменты М_к представляют непрерывные функции. Границами таких участков будут характерные сечения, в плоскостях которых дейст­вуют скручивающие моменты, а также концевые сечения. Заданный вал имеет три участка: АС=а, CD==b и ДВ==с (см. рис. 2, б).

Параллельно оси вала располагаем ось эпюры и наносим на нее положения характерных сечений. Построение эпюры будем производить последовательно по участкам. При этом условимся ординаты положительных М_к откладывать вверх, а отрицательных — вниз.

Участок АС. В поперечном сечении 1—1 участка АС взятом на некотором расстоянии х1 от граничного сечения А, при рассмотрении левой части вала (на нее действует только скручивающий момент М1, (см. рис. 2, а) крутящий момент будет

Читайте также: Подвесной подшипник карданного вала форд транзит замена

Здесь момент М, принят с плюсом, так как вызывает закручивание рассматриваемой части вала в районе сечения 1—1 (при ее мысленном закреплении по этому cечению) по часовой стрелке, если смотреть со стороны сечения.

Из выражения для М_к (х1) видно, что во всех поперечных сечениях от А до С крутящие моменты одинаковы и равны 2 М. Следовательно, для участка АС эпюра М_к ограничена прямой, параллельной оси (рис. 2, б).

Участок DB. В поперечном сечении 3—3 участка DB, взятом на произвольном расстоянии х3, oт граничного сечения В, при рассмотрении правой части вала (на нее действует только момент М4) крутящий момент будет

Здесь момент принят с минусом, так как вызывает закручивание рассматриваемой правой части вала в районе сечения 3—3 (при ее мысленном закреплении по этому сечению) против часовой стрелки, если смотреть со стороны сечения.

Из выражения для М_к (х3) видно, что во всех поперечных сечениях от В до D крутящие моменты одинаковы и равны —1,2 М. Так что и для участка DB эпюра Мк ограничена отрезком прямой, параллельной оси, но только в этом случае эпюра будет находиться под осью ввиду отрицательных значений крутящих моментов (см. рис. 2, в).

На построенной эпюре крутящих моментов под характерными сечениями вала получились „скачки», величины которых с учетом масштаба равны скручивающим моментам М1,М2,М3,М4 приложенным к этим сечениям.

Эпюра Мк дает наглядную картину распределения крутящих моментов по длине вала и позволяет указать поперечные сечения, в которых возникают наибольшие крутящие моменты. Для призматических валов такие сечения называют опасными (по ним может произойти разрушение вала), а действующие в них наибольшие моменты – расчетными.

Напряжения в поперечных сечениях круглого вала

Крутящий момент Мк является равнодействующим мо­ментом внутренних усилий, непрерывно распределенных по всему поперечному сечению вала и характеризуемых напряжениями.

Выясним характер этих напряжений, закон их распределения по сечению и их величину для вала круглого поперечного сечения.

Для этого сначала на поверхности вала круглого поперечного сечения, один конец которого закреплен, нанесем продольную риску по образующей А—В, две поперечные риски 1—1 и 2—2, представляющие собой следы поперечных сечений, и риску по радиусу О—В торцевого сечения и исследуем их поведение при кручении (рис. 3, а).

При кручении, например, моментом, приложенным к свободному концу вала (рис. 3, б), продольная риска А — В повернется относительно неподвижной точки А на некоторый угол γ и займет положение А—В’. Поперечные риски 1—1 и 2—2 повернутся вокруг оси на углы, определяемые дугами КК’ и DD’, т. е. повороты этих рисок будут прямо пропорциональны их расстояниям от закрепленного конца, общий вид рисок не изменится и расстояние между ними ввиду малости угла γ останется прежним. Риска по радиусу О—В, оставаясь прямой, вместе с торцевым сече­нием повернется на угол у и займет положение О—В’. На основании этого можно предположить, что и в других поперечных сечениях воображаемые радиусы, оставаясь пря­мыми, поворачиваются вместе с сечениями. Так, например, воображаемые радиусы О₁К и О₁Д, оставаясь прямыми, повернутся вместе с сечениями 1—1 и 2—2 и займут положения О₁К’ и О₁Д’.

Читайте также: Назначение валов в редукторе

Все это позволяет считать, что при кручении круглого вала происходит взаимный поворот его поперечных сечений; сами же сечения остаются плоскими, параллельными, и расстояние между ними не изменяется.

В любых точках поперечных сечений при кручении круглого вала возникают только касательные напряжения τ, направленные перпендикулярно к радиусам, проходящим через рассматриваемые точки.

При чистом сдвиге, согласно закону Гука,

где ρ – расстояние от рассматриваемой точки до центра сечения

Величина касательных напряжений в сечении зависит только от удаления точки от центра сечения

Т.О. касательные напряжения в какой-либо точке поперечного сечения круглого вала прямо пропорциональны расстоянию ρ от этой точки до центра сечения.

Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

Напряжения в поперечных сечениях вала

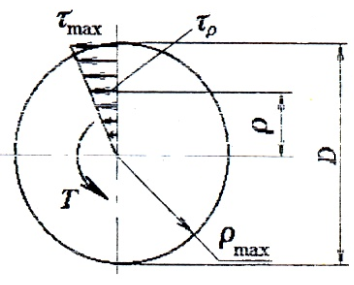
Крутящему моменту соответствуют касательные напряжения , которые распределяются по линейному закону вдоль диаметра, рис. 4. Величина касательных напряжений в любой точке поперечного сечения может быть определена по формуле:

I — полярный момент инерции.

Для круглого сечения полярный момент инерции равен:

где d — диаметр круглого сечения;

с — расстояние от центра круга (полюса) до точки, в которой определяется напряжение.

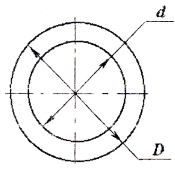
Для кольцевого сечения (рис. 6):

Из формулы (1) следует, что касательное напряжение в центре сечения равно нулю, а максимальные по величине напряжения действуют в точках контура сечения (так называемые «опасные точки»), т. е. при . Величина этих напряжений может быть определена по формуле:

где W — полярный момент сопротивления.

Рис. 5. Рис. 6.

где D — внешний диаметр кольца; с — отношение диаметров: .

Направление касательного напряжения в каждой точке сечения перпендикулярно радиусу (рис. 5).

Выражение крутящего момента через напряжения:

отражает его физический смысл: крутящий момент — есть момент результирующий пары внутренних касательных сил упругости, действующих в поперечном сечении вала.

Видео:Внутренные силы и напряжения в поперечных сечениях. Расчет на прочностьСкачать

iSopromat.ru

Кручением называется такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент T.

Брусья, испытывающие кручение, принято называть валами.

Видео:Основы Сопромата. НапряженияСкачать

Внутренний крутящий момент

Внутренние скручивающие моменты появляются под действием внешних крутящих моментов m_i, расположенных в плоскостях, перпендикулярных к продольной оси бруса.

Скручивающие моменты передаются на вал в местах посадки зубчатых колес, шкивов ременных передач и т.п.

Величина крутящего момента в любом сечении вала определяется методом сечений:

т.е. крутящий момент численно равен алгебраической сумме скручивающих моментов m_i, расположенных по одну сторону от рассматриваемого сечения.

Читайте также: Шлифовка длинных валов услуга

Правило знаков внутренних скручивающих моментов:
Положительными принимаются внутренние моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки, при рассмотрении со стороны отброшенной части вала.

В технике наиболее широко используются валы круглого поперечного сечения.

Теория кручения круглых валов основана на следующих гипотезах:

1. поперечное сечение, плоское до деформации вала, остается плоским и после деформации;
2. радиусы, проведенные мысленно в любом поперечном сечении, в процессе деформации вала не искривляются.

Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать

Напряжения при кручении

В поперечных сечениях вала при кручении имеют место только касательные напряжения.
Касательные напряжения, направленные перпендикулярно к радиусам, для произвольной точки, отстоящей на расстоянии ρ от центра, вычисляются по формуле:

где I_ρ — полярный момент инерции.
Эпюра касательных напряжений при кручении имеет следующий вид:

Касательные напряжения меняются по линейному закону и достигают максимального значения на контуре сечения при ρ= ρ_max:

Здесь:

— полярный момент сопротивления.
Геометрические характеристики сечений:
а) для полого вала:


б) для вала сплошного сечения (c=0)

в) для тонкостенной трубы (t 0,9)

где

— радиус срединной поверхности трубы.

Видео:Кручение. Часть 1 Общие сведенияСкачать

Деформации

Деформации валов при кручении заключаются в повороте одного сечения относительно другого.

Угол закручивания вала на длине Z определяется по формуле:

Если крутящий момент и величина GI_ρ, называемая жесткостью поперечного сечения при кручении, постоянны, для участка вала длиной l имеем:

Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания:

Расчет валов сводится к одновременному выполнению двух условий:

1. условию прочности:
   
2. условию жесткости:
   

Для стальных валов принимается:

• допускаемое касательное напряжение
  
• допускаемый относительный угол закручивания
  

Используя условия прочности и жесткости, как и при растяжении – сжатии можно решать три типа задач:

1. проверочный расчет, заключающийся в проверке выполнения условий прочности и жесткости при известных значениях крутящего момента, размеров и материала вала.
2. Проектировочный расчет, при котором вычисляются диаметры:
   
   при этом берется большее из найденных значений, а затем принимается стандартное значение по ГОСТ.
3. Определение грузоподъемности вала:
   • из условия прочности
     
   • из условия жесткости
     

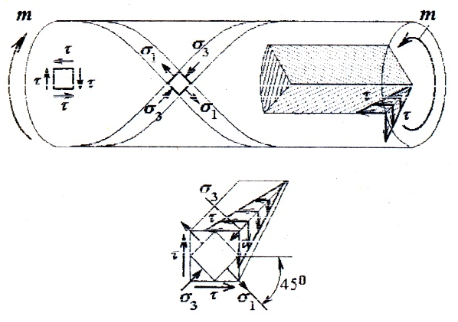
При кручении, наряду с касательными напряжениями в поперечных сечениях, в соответствии с законом парности, касательные напряжения возникают и в продольных сечениях. Таким образом, во всех точках вала имеет место чистый сдвиг.

Главные напряжения σ₁ = τ, σ₃ = -τ наклонены под углом α=±45 о к образующей.

Потенциальная энергия упругой деформации определяется по формуле

или для участка вала при постоянном T и GI_ρ

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

• Свежие записи
  • Чем отличается двухтактный мотор от четырехтактного
  • Сколько масла заливать в редуктор мотоблока
  • Какие моторы бывают у стиральных машин
  • Какие валы отсутствуют в двухвальной кпп
  • Как снять стопорную шайбу с вала

  
  

  источники:

  https://evakuatorinfo.ru/chto-takoe-napryazhenie-v-poperechnyh-secheniyah-vala

  💥 Видео

  НАПРЯЖЕНИЕ - САМОЕ ПРОСТОЕ ОБЪЯСНЕНИЕ В АНИМАЦИИ.Скачать

  

  Построение эпюры касательных напряженийСкачать

  

  Определение усилий, напряжений и перемещений. СопроматСкачать

  

  Урок 6. Что такое НАПРЯЖЕНИЕСкачать

  

  Кручение. Расчет составного вала кольцевого сечения.Скачать

  

  Построение эпюры крутящих моментовСкачать

  

  Основы Сопромата. Расчеты на прочность. Общая идеяСкачать

  

  Что такое напряжение? | Разность потенциалов | Электроника шаг за шагомСкачать

  

  Что такое НАПРЯЖЕНИЕ и в чем разница с током?Скачать

  

  Л 6 Карипбаева А Р КручениеСкачать

  

  Запас прочности и допускаемые напряженияСкачать

  

  Сопротивление материалов. Лекция: метод сеченийСкачать

  

  Сопромат. Практическое занятие №1.4Скачать

  

  Сопромат. Часть 1. Растяжение (сжатие). Построение эпюр продольных сил и нормальных напряжений.Скачать