Что такое жесткость поперечного сечения вала при кручении

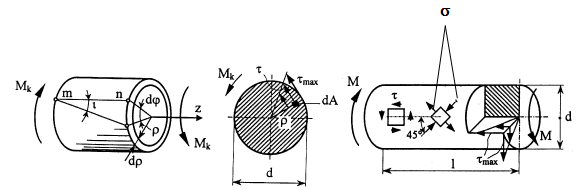
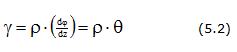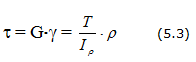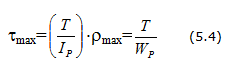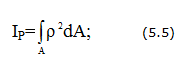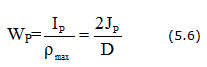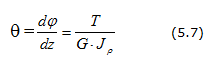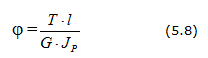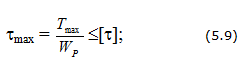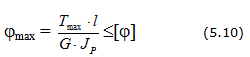Напряженное состояние, при котором на гранях элемента конструкции возникают только касательные напряжения, называют чистым сдвигом.

Закон Гука при сдвиге имеет вид:

Для изотропных материалов существует зависимость между константами упругости:

Видео:Кручение. Часть 6 Жесткость валаСкачать

Кручение

Кручением называется вид деформации, при котором в любом поперечном сечении бруса возникает только один крутящий момент.

Знак крутящего момента не имеет физического смысла.

Угол закручивания бруса определяется формулой:

Жесткостью сечения при кручении круглого бруса называется величина [GI_p]=H*м 2

Полярным моментом сопротивления сечения кручению называется величина:

Максимальные касательные напряжения достигаются на поверхности круглого бруса и равны:

Опасным сечением при кручении называется поперечное сечение бруса, в котором возникает максимальное касательное напряжение.

Угол закручивания бруса длиной l при постоянном крутящем моменте равен:

Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

Расчеты на прочность и жесткость при кручении.

1. При проверочном расчете определяется наибольшее касательное напряжение, которое сравнивается с допускаемым касательным напряжением:

2. При проектном расчете определяется площадь и диаметр опасного сечения стержня из условия:

3.При определении допускаемой нагрузки рассчитывается максимальный допускаемый крутящий момент:

1. Условие жесткости при кручении имеет вид:

2.Подбор поперечного сечения бруса осуществляется из условия:

Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать

iSopromat.ru

Для обеспечения прочности и жесткости вала при кручении, напряжения и деформации от крутящих моментов не должны превышать соответствующих допустимых значений.

Этот вид нагружения возникает при приложении к брусу пар сил, плоскости действия которых перпендикулярны его оси. Такие брусья принято называть валами.

Внешние пары, приложенные к валу, будем называть скручивающими моментами. Они могут быть сосредоточенными М₁, М₂, …, М_n или распределенными m по длине вала l .

Крутящий момент является равнодействующим моментом напряжений, возникающих в каком-либо сечении вала относительно его продольной оси.

Видео:Правило знаков при крученииСкачать

Внутренний крутящий момент

При определении величины крутящего момента используется метод сечений. Суть его заключается в следующем: рассекаем вал сечением и отбрасываем одну из частей вала, расположенную либо справа, либо слева от сечения.

Обычно отбрасывают ту часть, к которой приложено больше скручивающих пар. Действие отброшенной части на рассматриваемую заменяют внутренним силовым фактором – крутящим моментом T . Затем из условий равновесия остановленной части вала определяют крутящий момент:

Таким образом, крутящий момент в каком либо сечении вала является уравновешивающей парой сил всех внешних скручивающих пар, приложенных либо слева, либо справа от рассматриваемого сечения.

Видео:Сопромат. Практическое занятие №1.4Скачать

Напряжения при кручении

Распределение касательных напряжений

Максимальное касательное напряжение

Геометрические характеристики круглых сплошных сечений вала

Полярный момент сопротивления

Видео:Кручение. Расчет составного вала кольцевого сечения.Скачать

Деформации вала

Видео:11. Кручение ( практический курс по сопромату )Скачать

Условия прочности и жесткости вала

Расчет вала при кручении сводится к одновременному удовлетворению двух условий:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:12. Подбор сечения при кручении ( практический курс по сопромату )Скачать

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

Видео:Сопромат. Построение эпюр вала при кручении. Я в вк https://vk.com/id4682924Скачать

Набор студента для учёбы

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Видео:Понимание напряжений в балкахСкачать

5.6 Расчет на прочность и жесткость при кручении

Условие прочности при кручении:

Допускаемое касательное напряжение [τ] определяется как:

Читайте также: Готовые валы с подшипниками

Условие жесткости при кручении:

где [θ] – допускаемый относительный угол закручивания вала,

Видео:Расчет вала на изгиб с кручениемСкачать

Три типа задач расчета на прочность при кручении.

1 тип задач: проверочный расчет, выполняется по уравнению (5.29).

2 тип задач: проектный расчет или подбор сечений. В этом случае из условия прочности выражается геометрическая характеристика сечения- полярный момент сопротивления, а затем определяется диаметр вала:

3 тип задач: определение допускаемой нагрузки. В этом случае из условия прочности выражается крутящий момент:

В тех случаях, когда диаметр вала невелик, а длина его значительна, необходима проверка на жесткость по уравнению (5.31). Если условие не выполняется, то диаметр вала следует определить из условия жесткости.

Как показали эксперименты и точное решение задачи на кручение в теории упругости, все гипотезы, сформулированные ранее для стержня со сплошным круговым сечением, остаются справедливыми и для стержня кольцевого поперечного сечения.. Поэтому все выведенные ранее формулы пригодны для расчета стержня кольцевого сечения с той лишь разницей, что полярный момент инерции определяется как разность моментов инерции кругов с диаметрами D и d:

где , а момент сопротивления определяется по формуле:

Учитывая линейный характер изменения касательных напряжений по радиусу и связанное с этим лучшее использование материала, кольцевое сечение следует признать наиболее рациональным при кручении стержня. Коэффициент использования материала тем выше, чем меньше относительная толщина трубы.

Видео:Кручение валаСкачать

5.7 Анализ напряженного состояния и разрушения вала при кручении

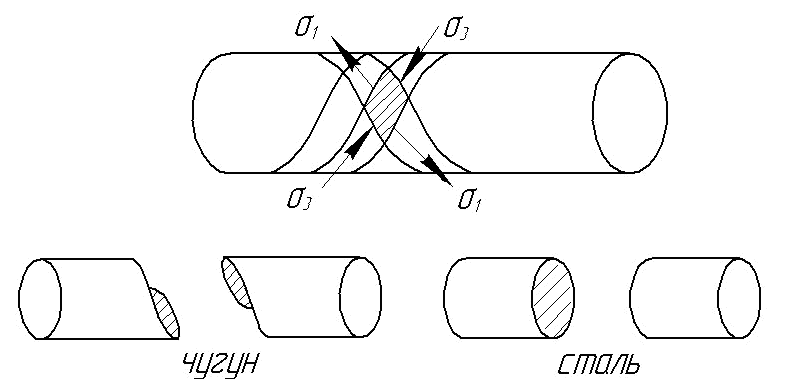
Ранее установлено, что в поперечных сечениях вала возникают только касательные напряжения. На основании закона парности касательных напряжений они возникают также и в продольных сечениях и изменяются по тому же закону, что и в поперечных (рис.5.10).

Главные площадки наклонены к площадкам чистого сдвига под углом 45 0 и образуют на поверхности вала винтовую линию, при этом в одном направлении волокна растянуты; в другом – сжаты.

Особенности напряженного состояния при кручении нашли отражение в характере разрушения стержней (рис.5.11). Хрупкие материалы, которые плохо работают на кручение, разрушаются по винтовой линии в направлении растягивающих напряжений. Пластичные материалы разрушаются при кручении по поперечным сечениям за счет максимальных касательных напряжений. Так, разрушение стержня из дерева, плохо работающего на скалывание вдоль волокон, происходит от продольных трещин.

Видео:Изгиб с кручениемСкачать

Расчет валов на кручение

Спроектировать ступенчатый вал равного сопротивления, .

1. Вычертить схему нагружения вала, построить эпюру крутящего момента.

2. Установить допускаемое касательное напряжение [τ] по третьей теории прочности и определить диаметр вала до стандартных размеров.

3. Построить эпюру угловых перемещений.

4. Для одного силового участка определить максимальное касательное напряжение, а также главные напряжения и показать их на выделенном элементе.

5. Провести проверку вала на жесткость.

Минимальное значение диаметра принять равным 10 мм.

Видео:Расчет валов круглого кольцевого поперечного сечения на кручениеСкачать

И ЖЕСТКОСТЬ ПРИ КРУЧЕНИИ

Сдвигом называют такой вид напряженного состояния, когда на гранях элемента действуют только касательные напряжения. Деформации, возникающие при сдвиге, называют угловыми деформациями или углом сдвига.

Кручением называют такой вид простого нагружения, при котором внешние пары сил действуют в плоскостях поперечных сечений. Стержень, работающий на кручение, называют валом.

В поперечных сечениях вала возникает только крутящий момент М_х., который в произвольном поперечном сечении численно равен алгебраической сумме всех внешних моментов, приложенных по одну сторону от рассматриваемого сечения и вращающих вокруг продольной оси х.

Читайте также: Гравер с гибким валом калибр

Между интенсивностью внешнего скручивающего момента m и внутреннего крутящего момента M имеется соотношение

Из геометрического смысла производной (первая производная равна тангенсу угла между касательной к кривой и осью

абсцисс) следуют правила для проверки соответствия эпюры крутящих моментов расчетной схеме такие же, как для растяжения.

При кручении круглого бруса в поперечных сечениях действуют и подлежат определению касательные напряжения, меняющиеся вдоль радиуса по линейному закону:

Здесь M_х – внутренний крутящий момент в сечении вала, ρ – полярная координата произвольной точки в поперечном сечении, J₀ – полярный момент инерции сечения. (Таким образом, в записи формулы использована полярная система координат.)

Наиболее опасными точками сечения вала, в которых действуют наибольшие касательные напряжения, являются точки около наружной поверхности (на контуре сечения), где

где W₀ – полярный момент сопротивления сечения.

Для кольцевого профиля (труба) снаружным диаметром Dивнутренним d соответствующие характеристики имеют вид

Условие прочности вала имеет вид

где[t] – допускаемое касательное напряжение, которое определяется аналогично допускаемому нормальному напряжению или приближенно [t] ≈ (0.5 0.6)[σ].

Если необходимо определить диаметр вала из условия прочности (26), то решение проводится относительно момента сопротивления:

Определение полного угла закручивания вала или угла поворота сечения вокруг продольной оси х проводят по закону Гука при кручении:

где G (МПа) – модуль упругости материала второго рода (модуль сдвига, модуль Стокса), i – номер участка.

Для валов с переменными параметрами перемещения вычисляются по формуле

При расчете валов наряду с выполнением условия прочности может потребоваться выполнение условия жесткости. Условие жесткости заключается в том, что максимальный относительный угол закручивания θ_max, то есть угол приходящийся на единицу длины вала, не должен превышать допустимых значений [θ].

Допустимый относительный угол закручивания устанавливается техническими условиями. Его величина для разных энергетических конструкций и различных режимов работы вала колеблется в достаточно широких пределах:

По условию жесткости возможно решение тех же трех вариантов задач, что и по условию прочности.

Расчетное соотношение для определения диаметра вала из условия жесткости приобретает вид:

При расчете бруса на прочность (27) и жесткость (30) из двух найденных значений диаметра следует принять то, которое удовлетворяет обоим условиям надежности, то есть большее.

Диаметры вала в местах посадки на него различных деталей (дисков, шкивов, подшипников и т.п.) округляют до ближайшего стандартного значения.

Для заданного вала (рис. 7,а), нагруженного скручивающими сосредоточенными и распределенными моментами, выполнить расчет на прочность и жесткость. Здесь принято М =m l.

Вычисляется из уравнения равновесия – по условию равенства нулю суммы моментов относительно оси вращения (10,4):

Вал имеет два участка. Следовательно, для построения эпюры внутренних крутящих моментов достаточно два раза применить метод сечений.

Для первого сечения (рис.7,б) для левой части вала уравнение равновесия имеет вид

(на эпюре наклонная прямая).

Читайте также: Что такое огас глушков валах

Рис. 7. Кручение (к примеру 2):

а – расчетная схема; б – рассматриваемые отсеченные части;

в – эпюра крутящих моментов; г – эпюра касательных напряжений;

д – эпюра угловых перемещений

На первом участке границы изменения x₁: . Подставляя эти значения, определяют величины моментов на границах участка:

Аналогично на втором участке (для левой части вала) = const ,

или (для правой части вала) .

Эпюра внутренних крутящих моментов приведена на рис.7,в. Согласно указанным ранее правилам на первом участке она ограничена наклонной прямой, а на втором – прямой параллельной оси.

Из эпюры видно, что максимальное значение момента |M_max| =2M (а не 3M). Именно для этого опасного значения и проводится последующий расчет на прочность.

В рассматриваемом примере эпюра максимальных касательных напряжений (рис. 7,г) качественно повторяет эпюру моментов M_x (рис. 7,в), так как вал имеет постоянное сечение по

длине. Условие прочности проверяется для опасного сечения, которое находится на границе между участками:

Если взять не сплошное, а кольцевое сечение, то при сохранении прежнего значения наружного диаметра, максимальные касательные напряжения существенно увеличиваются. Это объясняется уменьшением момента сопротивления.

Из условия прочности при кручении, как и при растяжении и сжатии, в зависимости от постановки задачи может быть определена допускаемая нагрузка:

В рассмотренном примере │M_х│= 2М. Следовательно, допустимая нагрузка на вал

Из условия прочности при кручении в зависимости от постановки задачи может быть определен диаметр вала по (25).

Определение полного угла закручивания вала или угла поворота сечения вокруг продольной оси х производят по закону Гука при кручении (28):

, (на эпюре парабола выпуклостью вверх):

Знаки перед слагаемыми соответствуют знакам внутренних крутящих моментов (рис.7,в). Физически φ₂ означает угол закручивания второго участка вала– угол поворота сечения В относительно А вокруг продольной оси под действием внешней нагрузки, а φ_ВО означает угол поворота сечения В относительно жесткой связи 0.

Эпюра перемещений приведена на рис. 7,д. На первом участке она ограничена выпуклой к оси абсцисс параболой, а на втором – наклонной прямой. Здесь, как и в случае расчета перемещений при растяжении, для проверки соответствия эпюры крутящих моментов расчетной схеме можно использовать геометрический смысл (по площади) эпюры моментов.

Вопросы для самопроверки

1. Что называется абсолютным и относительным сдвигом? 2. Что называется законом парности касательных напряжений при сдвиге? 3. Как формулируется закон Гука при сдвиге? 4. Как связаны между собой модуль продольной упругости, Е, и модуль сдвига, G? 5. Как производится расчет на прочность при сдвиге ? 6. Как распределены напряжения в поперечном сечении при сдвиге? 7. Что называют кручением? 8. Какие напряжения возникают в поперечном сечении круглого бруса при кручении? 9. Как определить величину напряжений при кручении? 10. Как определить допустимые напряжения при кручении? 11. Как определить полярный момент инерции и полярный момент сопротивления сечения при кручении? Какова их размерность? 12. Как определить угол закручивания бруса? 13. Как записать условие прочности при кручении? 14. В чем заключается расчет вала на жескость? 15. Как расчитывают валы на сложное сопротивление (изгиб совместно с кручением)?

• Свежие записи
  • Чем отличается двухтактный мотор от четырехтактного
  • Сколько масла заливать в редуктор мотоблока
  • Какие моторы бывают у стиральных машин
  • Какие валы отсутствуют в двухвальной кпп
  • Как снять стопорную шайбу с вала
  • Правообладателям
  • Политика конфиденциальности

  
  

  источники:

  https://evakuatorinfo.ru/chto-takoe-zhestkost-poperechnogo-secheniya-vala-pri-kruchenii

  📸 Видео

  Сопротивление материалов. Лекция: кручение круглого стержняСкачать

  

  Лекция Кручение.Скачать

  

  Кручение. Часть 1 Общие сведенияСкачать

  

  Обзор № 13 "Основы расчетов конструкций на прочность и жесткость"Скачать

  

  Основы Сопромата. Расчеты на прочность. Общая идеяСкачать

  

  Видеоурок 6. Расчеты на прочность и жесткость при изгибе.Скачать