Дан цилиндр радиус основания которого равен 10 концы отрезка

Видео:№530. Высота цилиндра равна 12 см, а радиус основания равен 10 см. Цилиндр пересеченСкачать

Высота цилиндра равна 15 см , радиус основания 10 см?

Высота цилиндра равна 15 см , радиус основания 10 см.

Дан отрезок , концы которого принадлежат окружностям обоих оснований и длина которого равна 3 корня из 41 см .

Найдите расстояние между данным отрезком и осью цилиндра.

Нарисуйте рисунок пожалуйста!

OA = R = 10см, OO1 = H = 15см, A1B = 3√41см

ΔА1ВА — прямоугольный, АА1 = ОО1

АВ = √(А1В — АА1) = √(369 — 225) = √144 = 12см

ОH — расстояние до сечения, а значит и до А1В

ОH — высота равнобедренного ΔАОВ

OH = √(OA² — AH²) = √(100 — 36) = √64 = 8см.

Видео:№527. Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус цилиндра равен г,Скачать

Ребяяят помогите с рисунком, ну и еслиРебяяят помогите с рисунком, ну и если можно то с решением : * * *Через хорду основания цилиндра, высота которого равна Н, арадиус основания — R, проведено сечени?

Ребяяят помогите с рисунком, ну и еслиРебяяят помогите с рисунком, ну и если можно то с решением : * * *

Через хорду основания цилиндра, высота которого равна Н, а

радиус основания — R, проведено сечение, параллельное оси цилиндра.

между радиусами, проведенные в концы данной хорды, равен 2ф.

а) площадь сечения цилиндра.

Б) угол между осью цилиндра и диагональю сечения.

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Диаметр основания цилиндра равен 1 м высота цилиндра равна длине окружности основания?

Диаметр основания цилиндра равен 1 м высота цилиндра равна длине окружности основания.

Найдите площадь боковой поверхности цилиндра.

Видео:№531. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельнойСкачать

Высота цилиндра равна 5 а радиус основания равен 26 площадь сечения цилиндра плоскостью проходящей параллельно оси цилиндра равна 100 найдите расстояние от плоскости сечения до центра основания цилинд?

Высота цилиндра равна 5 а радиус основания равен 26 площадь сечения цилиндра плоскостью проходящей параллельно оси цилиндра равна 100 найдите расстояние от плоскости сечения до центра основания цилиндра.

Видео:Видеоурок по математике "Цилиндр"Скачать

Сечение, параллельное оси цилиндра, отстает от его оси на расстояние, равное 3?

Сечение, параллельное оси цилиндра, отстает от его оси на расстояние, равное 3.

Найдите площадь сечения, если радиус основания цилиндра равен 5, а его высота — 10.

Видео:РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

Концы отрезка АВ лежат на окружностях оснований цилиндра?

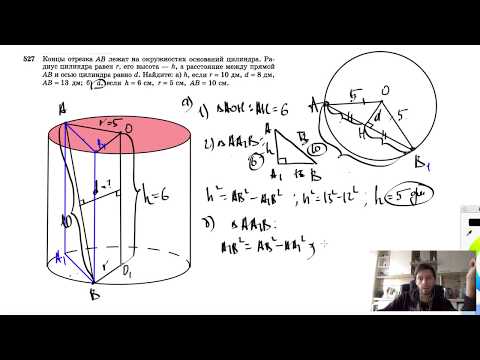
Концы отрезка АВ лежат на окружностях оснований цилиндра.

Радиус основания равен 5 см, высота цилиндра равна 6 см, АВ = 10 см.

Определите расстояние между прямой АВ и осью цилиндра.

Видео:№525. Площадь осевого сечения цилиндра равна 10 м2, а площадь основания — 5 м2.Скачать

Отрезок CD концы которого лежат на разных окружностях оснований цилиндра, пересекает ось цилиндра под углом 60 градусов?

Отрезок CD концы которого лежат на разных окружностях оснований цилиндра, пересекает ось цилиндра под углом 60 градусов.

Найдите объём цилиндра, если длина отрезка CD равна 8 см.

Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Длина окружности в основании цилиндра равна 12π?

Длина окружности в основании цилиндра равна 12π.

Читайте также: Прямая призма найдите объем цилиндра описанного около призмы

Чему равен радиус цилиндра?

Площадь основания цилиндра равна 9π м2, а площадь осевого сечения равна 12 м2.

Видео:ЕГЭ БАЗА 16 номер Радиус основания цилиндра равен 15, а его образующая равна 14Скачать

Отрезок CD 25 см, его концы лежат на разных окружностях оснований цилиндра?

Отрезок CD 25 см, его концы лежат на разных окружностях оснований цилиндра.

Найдите расстояние от отрезка CD до оси цилиндра, если его высота 7см а диаметр основания 26 см.

Видео:№523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высотуСкачать

На окружностях обоих оснований цилиндра выбрано по точке, расстояние между которыми равно 13?

На окружностях обоих оснований цилиндра выбрано по точке, расстояние между которыми равно 13.

Найдите расстояние от этого отрезка до оси цилиндра , если высота цилиндра равна 5 , а радиус основания равен 10.

Видео:9 вариант ЕГЭ Ященко 2024 математика профильный уровень 🔴Скачать

Диаметр основания цилиндра равен 1 метр, высота цилиндра равна длине окружности основания?

Диаметр основания цилиндра равен 1 метр, высота цилиндра равна длине окружности основания.

Найдите площадь боковой поверхности цилиндра.

На этой странице вы найдете ответ на вопрос Высота цилиндра равна 15 см , радиус основания 10 см?. Вопрос соответствует категории Геометрия и уровню подготовки учащихся 10 — 11 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

В окружности проводим два взаимно — перпендикулярных диаметра. Точки пересечения с окружностью соединяешь. Получается правильный четырёхугольник.

3. Движения литосферных плит. Силы, способные двигать плиты литосферы, зарождаются внутри нашей планеты. Поэтому их называютвнутренними силами Земли. Они возникают при распаде радиоактивных веществ и перемещения расплава в верхней мантии. Внутрен..

DE – средняя линия тр — ка DE = АС : 2 = 80 : 2 = 40.

Это средняя линия треугольника и она равна половине основания следовательно DE = 40 см.

Если первый угол 90гр. , второй 60 гр. , то третий будет 30 гр. А катет , лежащий против угла 30 гр равен половине гипотенузы Пусть катет будет х, тогда гипотенуза будет 2х х + 2х = 18 3х = 18 х = 6(катет) гипотенуза = 2х = 12.

Пускай катет — х, гипотенуза — y у = 2х х + 2х = 18 х = 6 см — катет 6 * 2 = 12 см — гипотенуза.

Треугольник имеет три угла и их сумма равна 180 градусам.

Хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз.

Обозначим катеты 5х и 12 х. В прямоугольном треугольнике гипотенуза равна двум медианам, то есть 52 см. По Пифагору 52² = (5х)² + (12х)² 2704 = 25х² + 144х², 2704 = 169х², х = √(2704 / 169) = √16 = 4 см. Тогда катеты равны 5 * 4 = 20 см и 12 * 4 =..

В трапеции две прямые папаллельны, значит сумма односторонних углов 180° пусть х — больший угол у — меньший угол х — у = 84 по условию х + у = 180 углы при каждом из оснований равны регаем систему и получаем х = 132 у = 48.

Видео:Профильный ЕГЭ 2024 математика Ященко. Вариант 10Скачать

Дан цилиндр радиус основания которого равен 10 концы отрезка

Высота цилиндра равна 5, а радиус основания 10.

а) Докажите, что площадь боковой поверхности цилиндра равна площади его основания.

б) Найдите площадь сечения цилиндра плоскостью, проходящей параллельно оси цилиндра на расстоянии 6 от неё.

а) Вспомним, что площадь боковой поверхности цилиндра вычисляется по формуле , где — радиус основания, — высота цилиндра. В данном случае , поэтому , откуда и следует требуемое.

б) Сечение цилиндра плоскостью, проходящей параллельно его оси OO₁, — прямоугольник ABB₁A₁ (O и AB — соответственно центр и хорда нижнего основания цилиндра), AA₁ = 5. Расстояние от оси цилиндра до плоскости сечения равно высоте OH треугольника OAB. OA = OB = 10, OH = 6, откуда

Читайте также: Индикатор положения поршня в цилиндре

В условии сказано, что дан цилиндр: «Высота цилиндра. «, а в решении рассмотрен прямой цилиндр. Действительно, ответ такой же получится при решении задачи с наклонным цилиндром, но тем не менее, в сечении образуется параллелограмм, а не прямоугольник: прямая АА1 параллельна и равна прямой ВВ1, как образующие, которые параллельны, в свою очередь оси цилиндра — прямой ОО1. По признаку параллельности прямой и плоскости получаем, что ОО1 параллельна плоскости (АА1ВВ1). И уже нельзя говорить, что ОО1 является высотой, ведь цилиндр может быть и наклонным. Прямая ОО1 является осью цилиндра. А условная прямая О1М может являться высотой цилиндра (точка М может совпасть с точкой О, если цилиндр прямой). Она будет являться и высотой параллелограмма (это может быть и прямоугольник, который по определению также является параллелограммом).

Таким образом, ответ хотя и верный, но рассмотрено частное решение данной задачи. Либо составители допустили ошибку не указав, что дан прямой цилиндр (в 2018-ом же писали: «. образующая перпендикулярна плоскости основания»), либо решение данной задачи следует подправить.

В школьном курсе задачи о наклонных цилиндрах не рассматриваются.

Видео:№529. Высота цилиндра равна 8 см, радиус равен 5 см. Найдите площадь сечения цилиндраСкачать

Презентация к уроку геометрии «Цилиндр. Решение задач» (11 класс)

Ищем педагогов в команду «Инфоурок»

Описание презентации по отдельным слайдам:

Филиал ОГБОУ СПО «Рязанский педагогический колледж» в г.Касимове Презентация к уроку геометрии Цилиндр. Решение задач Подготовила преподаватель И.И.Колоколенкова

Цели урока: формировать навыки решения задач на нахождение элементов цилиндра, площади поверхности цилиндра; закрепить знания, умения учащихся по изучаемой теме; развивать самостоятельность учащихся в работе над задачами.

План урока 1. Организационный момент 2. Актуализация знаний: а)Устная работа с классом. I. Вопросы. II.Решение задач по готовому чертежу б) Проверка домашнего задания (три ученика работали у доски во время устной работы класса). 3. Фронтальная работа по слайдам 4. Работа в группах. Решение задач по готовым чертежам. 5. Физкультминутка. 6.Разноуровневая самостоятельная работа 7. Подведение итогов урока

Устная работа с классом а)Вопросы 1. Укажите среди окружающих вас предметов объекты, имеющие цилиндрическую форму. 2. Дайте определение цилиндра и его основных элементов. 3. Что такое осевое сечение цилиндра? Каков его вид? 4. Может ли осевое сечение быть: а) прямоугольником; б) квадратом; в) трапецией? Почему? 5. Цилиндр катится по плоскости. Какая фигура получается при движении его оси?

Б)Решение задачи по готовому чертежу (устно). Назовите элементы цилиндра Найти площадь полной поверхности цилиндра. ВС = 5 1. ∆АВС — прямоугольный. 2. Так как 6 слайд

Фронтальная работа по слайдам

Концы отрезка АВ, равного а, лежат на окружностях оснований цилиндра. Радиус цилиндра равен r, высота равна h, а расстояние между прямой АВ и осью 001 цилиндра равно d. 1. Объясните, как построить отрезок, длина которого равна расстоянию между скрещивающимися прямыми АВ и 001. 2. Составьте (и объясните) план нахождения величины d по заданным величинам а, h, r. 3. Составьте (и объясните) план нахождения h по заданным величинам а, r, d.

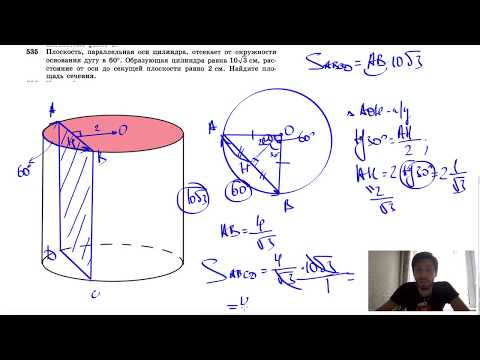
Слайд 2 Плоскость γ, параллельная оси цилиндра, отсекает от окружности основания дугу AmD с градусной мерой α. Радиус цилиндра равен а, высота равна h, расстояние между осью ОО1 цилиндра и плоскостью γ равно d. 1. Докажите, что сечение цилиндра плоскостью γ есть прямоугольник. 2. Объясните, как построить отрезок, длина которого равна расстоянию между осью цилиндра и секущей плоскостью. 3. Найдите AD, если а =10 см, α = 60° (другие варианты: α = 90°, α =120°). 4. Составьте (и объясните) план вычисления площади сечения по данным α , h, d.

Работа в группах. Решение задач по готовым чертежам

Читайте также: Задний тормозной цилиндр blazer

Задача №1. 1. OD = R, AD = 3. 2. ∆ADС – прямоугольный,так как AD = 4, то АС = 5 (пифагорова тройка). (Ответ: 5.)

Задача № 2 1. ∆ АВС — прямоугольный. 2. Так как 12 слайд

Задача № 3 1. ∆ АА1 В — прямоугольный; по теореме Пифагора АВ2 = АА12 + А1В2, 172 = 152 + ВА 12 , ВА1 2 = 172-152 = (17- 15)(7 + 15) = 2 • 32 = 64, А1В = 8 ДП: ОК, К – середина BA1 2. ОК ┴ А 1 В (так как ОК — расстояние между ОО1 и АВ: ОК ┴ ОО1 => ОК ┴ АА1 => ОК ┴ ( АА1В) => ОК ┴ А В. OK ┴A1B 3. По теореме Пифагора из ∆ A1 КО: ОА1 2 = ОК2 + А1К2, ОК= 25-16, ОК2 = 9, ОК =3. Дано: О1А = 5, АА1 = 15, АВ = 17. Найти: расстояние между ОО1 и АВ.

Задача №4 АО = 5 — дополнительное построение. AD = 2*(√25-9) = 2* √16 = 2*4 = 8. ABCD — прямоугольник. 4. SABCD = АВ • AD SABCD = 10 • 8 = 80. (Ответ: 80.) Найти: SABCD,

Задача №5 Дано: Sбок./Sосн. =1/2 Найти: H/2R Решение: 1. Sбок./Sосн = 2πRH/πR2 = 2H/R = ½. 2. 2H/R = ½. ═ H/2R = 1/8.

Задача № 6 Дано: ABCD — осевое сечение. Найти: Sбок./SABCD Решение: 1. Sбок.= 2πRH, ABCD — прямоугольник. 2. SABCD = AD • АВ, SABCD = 2R * Н. 3. Sбок./SABCD = = 2πRH/2RH = π (Ответ: π.).

Физкультминутка Мы с вами хорошо поработали, повторили всё необходимое. Прежде чем выполнить самостоятельную работу проведём физкультминутку. Сядьте удобнее, расслабьтесь. Каждое задание выполняем по 10 раз. Обведите верхнее основание цилиндра глазами по часовой стрелке, а нижнее – против часовой стрелки. Проведите глазами по оси цилиндра сверху вниз. Проведите глазами по диаметру справа налево. Закройте глаза. Откройте глаза. С новыми силами приступаем к работе.

Разноуровневая самостоятельная работа

1уровень Вариант I 1. Радиус цилиндра равен 10 см. Сечение, параллельное оси цилиндра и уда­ленное от нее на 8 см, имеет форму квадрата. Найти площадь сечения. 2. Диагональ осевого сечения цилиндра равна 8 √2 дм и образует с плоскостью ос­нования цилиндра угол 45°. Найдите площадь полной поверхности цилиндра. Вариант II 1. Высота цилиндра равна 16 см. На расстоянии 6 см от оси цилиндра проведе­но сечение, параллельное оси цилиндра и имеющее форму квадрата. Найди­те радиус цилиндра. 2. Диагональ осевого сечения цилиндра равна 8 дм и составляет с образующей угол 60°. Найдите площадь полной поверхности цилиндра. II уровень Вариант I 1. Прямоугольник вращается вокруг одной из своих сторон, равной 5 см. Пло­щадь боковой поверхности цилиндра, полученного при вращении, равна 100π см2. Найдите площадь прямоугольника. 2. Хорда нижнего основания цилиндра отсекает от окружности основания дугу в 120°. Отрезок, соединяющий центр верхнего основания с серединой данной хорды, равен 4√2 см и образует с плоскостью основания угол 45°. Найдите площадь осевого сечения цилиндра. Вариант II 1. Прямоугольник, одна из сторон которого равна 5 см, вращается вокруг неиз­вестной стороны. Найдите площадь прямоугольника, если площадь боковой поверхности цилиндра, полученного при вращении, равна 60π см2. 2. Хорда нижнего основания цилиндра удалена от центра нижнего основания на 2√3 см и отсекает от окружности основания дугу в 60°. Отрезок, соеди­няющий центр верхнего основания с одним из концов данной хорды, образу­ет с осью цилиндра угол 45°. Найдите площадь осевого сечения цилиндра.

Подведение итогов урока на уроке было интересно и все понятно на уроке было интересно, но возникли затруднения на уроке было все понятно, но неинтересно на уроке ничего не заинтересовало на уроке было все непонятно и неинтересно

Домашнее задание П. 53, 54. 1 уровень — № 527, 531. II уровень — № 531, 544. III уровень — № 544, 601.

🌟 Видео

№535. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 60Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Цилиндр и конус имеют общее основание и высоту. Высота цилиндра равна радиусу основания... (ЕГЭ)Скачать

№521. Докажите, что осевое сечение цилиндра является прямоугольником, две противоположныеСкачать