- Задания. 4.1.Дан цилиндр с радиусом основания R и высотой H
- Как посчитать объем цилиндра
- Онлайн калькулятор
- Зная радиус r и высоту h
- Формула
- Пример
- Зная диаметр d и высоту h
- Формула
- Пример
- Зная площадь основания So и высоту h
- Формула
- Пример
- Зная площадь боковой поверхности Sb и высоту h
- Формула
- Пример
- Тригонометрия
- Ещё по теме
- Дан цилиндр радиуса r с высотой h
- По заданной высоте h и радиусу основания r вычислить площадь боковой поверхности S=2πrh и объем V=nr2 h бочки
- 📹 Видео
Видео:🔴 Даны два цилиндра. Радиус основания и высота ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Задания. 4.1.Дан цилиндр с радиусом основания R и высотой H
4.1.Дан цилиндр с радиусом основания R и высотой H. Вычислить:
· площадь боковой поверхности SB=2*π*R*H;
· площадь полной поверхности SP=SB+2*SO;
Если SO>2, выдать сообщение «Площадь основания велика» и объём V не вычислять.
4.2. Найти действительные корни x1 и x2 квадратного уравнения ax 2 +bx+c=0 по заданным значениям коэффициентов a, b, c. Если дискриминант D=b 2 —4a*c≥0, то вычислить корни по формулам x1= и x2= . Если D 7, то выдать сообщение «Длина диагонали велика» и остальные величины не вычислять.
4.4. В правильной треугольной пирамиде заданы сторона основания a и высота h. Вычислить:
· длину бокового ребра ;
· радиус описанного около пирамиды шара ;
· угол наклона боковой грани к основанию .
Если b>10, то выдать сообщение «Длина бокового ребра велика» и остальное не считать.
4.5. Задан конус с радиусом основания R и высотой H. Вычислить:
· площадь основания SO= π*R 2 ;
· площадь боковой поверхности SB= π*R* ;
· площадь полной поверхности SP=SO+SB;
Если SO>2, то выдать сообщение «Площадь основания велика» и объём не считать.
4.6. Вычислить активное давление грунта на глубине z
= , где –коэффициент активного давления грунта; –средний удельный вес грунта; –угол внутреннего трения; c–удельное сцепление.
Если >1, то выдать сообщение «Коэффициент активного давления грунта велик» и не считать.
4.7. Фундамент сооружения имеет в плане размеры A и B. Размеры искусственного основания F определяются из выражения:
, где C=0,1*B.
Если C 10, то выдать сообщение «Длина диагонали велика» и остальное не считать.
4.9. Дана правильная четырёхугольная пирамида со стороной основания a и высотой h. Вычислить:
· длину бокового ребра ;
· угол наклона боковой грани к основанию ;
· радиус описанного около пирамиды шара .
Если b>10, то выдать сообщение «Длина бокового ребра велика» и остальное не считать.
4.10. Дана правильная четырёхугольная призма с высотой H и радиусом R окружности, описанной вокруг основания призмы. Вычислить :
Читайте также: Неравномерная работа цилиндров причина
· площадь боковой поверхности призмы SB=4 *R*H;
· площадь полной поверхности SP=SB+SO;
Если SO>2, то выдать сообщение «Площадь основания велика» и объём V не считать.
Задание 5.Решение систем линейных уравнений методом обратной матрицы и специальными средствами Excel.
Видео:Видеоурок по математике "Цилиндр"Скачать

Как посчитать объем цилиндра
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Онлайн калькулятор
Найти чему равен объем цилиндра (V) можно зная (либо-либо):
- радиус r и высоту h цилиндра
- диаметр d и высоту h цилиндра
- площадь основания So и высоту h цилиндра
- площадь боковой поверхности Sb и высоту h цилиндра
Подставьте значения в соответствующие поля и получите результат.
Зная радиус r и высоту h
Чему равен объем цилиндра V если известны его радиус r и высота h?
Формула
Пример
Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:
V = 3.14156 ⋅ 2 2 ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см 3
Зная диаметр d и высоту h
Чему равен объем цилиндра V если известны его диаметр d и высота h?
Формула
Пример
Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:
V = 3.14156 ⋅ ( 1 /2) 2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см 3
Зная площадь основания So и высоту h
Чему равен объем цилиндра V если известны его площадь основания So и высота h?
Формула
Пример
Если цилиндр имеет высоту h = 10 см, а площадь его основания So = 5 см 2 , то:
Зная площадь боковой поверхности Sb и высоту h
Чему равен объем цилиндра V если известны его площадь боковой поверхности Sb и высота h?
Формула
Пример
Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности Sb = 30 см 2 , то:
V = 30 2 / 4 ⋅ 3.14⋅ 5 = 900 /62.8 = 14.33 см 3
Видео:Задание 2 ЕГЭ профиль (Стереометрия) по сборнику Ященко 2023Скачать

Тригонометрия
Рис.9 Оптимальная форма цилиндра при заданном объеме позволяет уменьшить расходы на материалы. Поэтому такая задача актуальна, например, при строительстве нефтехранилищ (рисунок \(9\)).
Пусть \(H\) − высота цилиндра, а \(R\) − радиус его основания. Объем и полная площадь поверхности цилиндра вычисляются по формулам \[V = \pi H,\;\;\;S = 2\pi + 2\pi RH.\] В качестве независимой переменной выберем радиус основания \(R.\) Выразим \(H\) через \(R\) (при заданном объеме \(V\) ): \[H = \frac >>.\] Исследуем площадь поверхности \(S\left( R \right)\) на экстремум. \[ + 2\pi RH > = + 2\pi R \cdot \frac >> > = + \frac > .> \] Вычисляем производную: \[ + \frac > > \right)^\prime > > = > >> > = — 2V>> >>.> \] Находим стационарные точки: \[ \;\; — 2V>> >> = 0,>\;\; > — 2V = 0>\\ \ne 0> \end ,> \right.>\;\; >>>.> \] Данное значение \(R\) соответствует минимальной площади поверхности \(S\left( R \right),\) поскольку при переходе через эту точку производная меняет знак с минуса на плюс.
Читайте также: Масло в цилиндрах компрессия в норме
Ещё по теме
Дан ромб с диагоналями \(d1=5\) см и \(d2=4\). Найти площадь ромба.
Найдите \( \cos \alpha \) и \( ctg \alpha \) , если \( \sin \alpha=\dfrac \) и \( \dfrac .
Найти координаты точки на единичной окружности, полученной поворотом точки \( A\left( 1;0 \right) \) на \( \dfrac \) .
Основания равнобедренной (равнобокой) трапеции равны 8 и 20 сантиметров. Боковая сторона равна 10 см. Найдите площадь трапеции, подобной данной, которая имеет высоту 12 см.
Найти координаты точки на единичной окружности, полученной поворотом точки \( A\left( 1;0 \right) \) на \( 750<>^\circ \) .
\( A( _ >; _ >)=A(-7;6) \) — центр окружности. Радиус окружности равен \( 3 \) . Необходимо найти координаты точки \( P \) , полученной поворотом начального радиус-вектора на \( P \) .
Окно имеет форму прямоугольника, ограниченного сверху полукругом (рисунок \(3\)). Периметр окна равен \(P.\) Определить радиус полукруга \(R,\) при котором площадь окна является наибольшей.
Диагональ равнобокой трапеции является биссектрисой ее острого угла и делит среднюю линию трапеции на отрезки длиной 15 см и 33 см. Вычислить (в см 2 ) площадь трапеции.
Найти координаты точки на единичной окружности, полученной поворотом точки \( A\left( 1;0 \right) \) на \( -225<>^\circ \) .
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Видео:11 класс, 32 урок, Объем цилиндраСкачать

Дан цилиндр радиуса r с высотой h
В одном основании прямого кругового цилиндра с высотой 3 и радиусом основания 8 проведена хорда AB, равная радиусу основания, а в другом его основании проведён диаметр CD, перпендикулярный AB. Построено сечение ABNM, проходящее через прямую AB перпендикулярно прямой CD так, что точка C и центр основания цилиндра, в котором проведён диаметр CD, лежат с одной стороны от сечения.
а) Докажите, что диагонали этого сечения равны между собой.
б) Найдите объём пирамиды CABNM.
а) Для построения сечения опустим перпендикуляры AM и BN на второе основание цилиндра. Отрезки AM и BN параллельны и равны, значит, ABNM — параллелограмм. Так как прямые AM и BN перпендикулярны основаниям цилиндра и, в частности, прямой AB, параллелограмм ABNM является прямоугольником. Отрезки AN и BM равны как диагонали прямоугольника, что и требовалось доказать.
Читайте также: Где находится сливная пробка блока цилиндров ниссан
б) Площадь прямоугольника ABNM равна 3 · 8 = 24. Пусть H — точка пересечения отрезков NM и CD. Отрезок OH равен Высота CH пирамиды CABNM равна Следовательно, объём пирамиды CABNM равен:
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
Видео:Цилиндр и конус имеют общее основание и высоту. Высота цилиндра равна радиусу основания... (ЕГЭ)Скачать

По заданной высоте h и радиусу основания r вычислить площадь боковой поверхности S=2πrh и объем V=nr2 h бочки
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Вычислить площадь боковой поверхности и объём по заданной высоте h и радиусу r
Помогите, пожалуйста, написать программу по задаче: Вычислите площадь боковой поверхности s=2пrh и.
вычислить площадь поверхности и объем цилиндра по радиусу основания и высоте.
Помогите пожалуйста вычислить площадь поверхности и объем цилиндра по радиусу основания и высоте.
Вычислить площадь боковой поверхности S = 2πrh и объем V = πr2h бочки по заданной высотой h и радиусом основания r
Вычислить площадь боковой поверхности S = 2πrh и объем V = πr2h бочки по заданной высотой h.
Вычислить площадь поверхности и объем конуса по радиусу его основания и высоте
1. Составить программу по вычислению полной поверхности и объема конуса по радиусу его основания и.
По заданной высоте h и радиусу основания r вычислить площадь б
Составить программу, задав исходные данные самостоятельно помогите решить это
Вычислить площадь основания, объем и площадь боковой поверхности цилиндра
В цилиндре с радиусом основания R и высотой H вычислить площадь основания,обьем и площадь боковой.
В цилиндре с радиусом основания R и высотой H вычислить площадь основания,обьем и площадь боковой поверхности
В цилиндре с радиусом основания R и высотой H вычислить площадь основания,обьем и площадь боковой.
Вычислить объем цилиндра по известному радиусу основания и высоте
Написать программу, вычисляющую объем цилиндра по известному радиусу основания и высоте. Расчет.
📹 Видео
11 класс. Геометрия. Объем цилиндраСкачать

Егэ.11кл. Объём первого цилиндра равен 12 м³, у второго цилиндра высота в 3 раза больше,а основаниеСкачать

ЗАДАНИЕ 8 из ЕГЭ_53Скачать

№537. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длинеСкачать

Объем цилиндра.Скачать

11 класс, 15 урок, Площадь поверхности цилиндраСкачать

9 класс, 41 урок, ЦилиндрСкачать

Все Задания 3 ЕГЭ 2024 ПРОФИЛЬ из Банка ФИПИ (Математика Школа Пифагора)Скачать

Задания 11, 13 (часть 4) | ЕГЭ 2024 Математика (база) | Цилиндр, конусСкачать

Один больше другого? /ЦИЛИНДРЫ - СТЕРЕОМЕТРИЯ / ЕГЭ #72403Скачать

Задачи на цилиндр. Объем цилиндра - bezbotvyСкачать

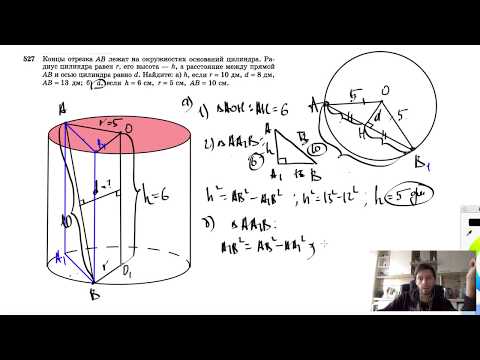
№527. Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус цилиндра равен г,Скачать
Задание 8 ЕГЭ по математикеСкачать

11 класс объем цилиндраСкачать





