- ПОМОГИЕ СРОЧНО ПОЖАЛУЙСТА. Умоляю или Кирдык !!Разверткой боковой поверхности цилиндра служит прямоугольник АВСD, AC =4см. Угол CAD =30 градусов. Найти площадь полной поверхности цилиндра, если высота =СD.
- Презентация к уроку геометрии «Цилиндр. Решение задач» (11 класс)
- Геометрия сборник с решениями (стр. 3 )
- 📸 Видео
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

ПОМОГИЕ СРОЧНО ПОЖАЛУЙСТА. Умоляю или Кирдык !!Разверткой боковой поверхности цилиндра служит прямоугольник АВСD, AC =4см. Угол CAD =30 градусов. Найти площадь полной поверхности цилиндра, если высота =СD.
В развертке CD — высота цилиндра, сторона AD равна длине окружности основания.
Из прямоугольного треугольника ACD:
CD = AC · sin 30° = 4 · 1/2 = 2 см
AD = AC · cos 30° = 4 · √3/2 = 2√3 см
Тогда площадь боковой поверхности:
Sбок = Sabcd = CD · AD = 2 · 2√3 = 4√3 см²
Длина окружности основания:
Sпов = 4√3 + 2 · 3/π = 4√3 + 6/π см²
боковая сторона 5,2 см; основание 3,2 см
Р=13,6см,основа хсм, боковая сторона х+2см, составляєм уровнение.
х+х+2+х+2=13,6; 3х+4=13,6; 3х=13,6-4, 3х=9,6, х=9,6:3=3,2см; 3,2+2=5,2см.
СВ- гипотенуза, АС и ВА — катеты
sin ∠АВС=0,8
АВ:СВ=0,8
Пусть коэффициент этого отношения х.
Тогда АВ=8х, ВС=10х
По теореме Пифагора
СВ²-ВА²=АС²
100х²-64х²=144
36х²=144
х²=4
х=2
ВС=2*10=20
———————————-
2
)По свойству углов при пересечении параллельных прямых секущей
биссектриса АК угла А образует со сторонами параллелограмма равнобедренный треугольник АВК, так как углы, отмеченны на рисунке как
а ∠1 является половиной ∠А
Отсюда ∠ А=2*35=70°, а так как сумма углов при одной стороне параллелограмма равна 180°, то
∠В=180°-70°=110°
Ответ:
∠А=∠С=70°
∠В=∠D=110°
Видео:Цилиндр - расчёт площади, объёма.Скачать

Презентация к уроку геометрии «Цилиндр. Решение задач» (11 класс)
Ищем педагогов в команду «Инфоурок»
Описание презентации по отдельным слайдам:
Филиал ОГБОУ СПО «Рязанский педагогический колледж» в г.Касимове Презентация к уроку геометрии Цилиндр. Решение задач Подготовила преподаватель И.И.Колоколенкова
Цели урока: формировать навыки решения задач на нахождение элементов цилиндра, площади поверхности цилиндра; закрепить знания, умения учащихся по изучаемой теме; развивать самостоятельность учащихся в работе над задачами.
План урока 1. Организационный момент 2. Актуализация знаний: а)Устная работа с классом. I. Вопросы. II.Решение задач по готовому чертежу б) Проверка домашнего задания (три ученика работали у доски во время устной работы класса). 3. Фронтальная работа по слайдам 4. Работа в группах. Решение задач по готовым чертежам. 5. Физкультминутка. 6.Разноуровневая самостоятельная работа 7. Подведение итогов урока
Устная работа с классом а)Вопросы 1. Укажите среди окружающих вас предметов объекты, имеющие цилиндрическую форму. 2. Дайте определение цилиндра и его основных элементов. 3. Что такое осевое сечение цилиндра? Каков его вид? 4. Может ли осевое сечение быть: а) прямоугольником; б) квадратом; в) трапецией? Почему? 5. Цилиндр катится по плоскости. Какая фигура получается при движении его оси?
Б)Решение задачи по готовому чертежу (устно). Назовите элементы цилиндра Найти площадь полной поверхности цилиндра. ВС = 5 1. ∆АВС — прямоугольный. 2. Так как 6 слайд
Фронтальная работа по слайдам
Концы отрезка АВ, равного а, лежат на окружностях оснований цилиндра. Радиус цилиндра равен r, высота равна h, а расстояние между прямой АВ и осью 001 цилиндра равно d. 1. Объясните, как построить отрезок, длина которого равна расстоянию между скрещивающимися прямыми АВ и 001. 2. Составьте (и объясните) план нахождения величины d по заданным величинам а, h, r. 3. Составьте (и объясните) план нахождения h по заданным величинам а, r, d.
Слайд 2 Плоскость γ, параллельная оси цилиндра, отсекает от окружности основания дугу AmD с градусной мерой α. Радиус цилиндра равен а, высота равна h, расстояние между осью ОО1 цилиндра и плоскостью γ равно d. 1. Докажите, что сечение цилиндра плоскостью γ есть прямоугольник. 2. Объясните, как построить отрезок, длина которого равна расстоянию между осью цилиндра и секущей плоскостью. 3. Найдите AD, если а =10 см, α = 60° (другие варианты: α = 90°, α =120°). 4. Составьте (и объясните) план вычисления площади сечения по данным α , h, d.
Читайте также: Расположение поршней в блоке цилиндров
Работа в группах. Решение задач по готовым чертежам
Задача №1. 1. OD = R, AD = 3. 2. ∆ADС – прямоугольный,так как AD = 4, то АС = 5 (пифагорова тройка). (Ответ: 5.)
Задача № 2 1. ∆ АВС — прямоугольный. 2. Так как 12 слайд
Задача № 3 1. ∆ АА1 В — прямоугольный; по теореме Пифагора АВ2 = АА12 + А1В2, 172 = 152 + ВА 12 , ВА1 2 = 172-152 = (17- 15)(7 + 15) = 2 • 32 = 64, А1В = 8 ДП: ОК, К – середина BA1 2. ОК ┴ А 1 В (так как ОК — расстояние между ОО1 и АВ: ОК ┴ ОО1 => ОК ┴ АА1 => ОК ┴ ( АА1В) => ОК ┴ А В. OK ┴A1B 3. По теореме Пифагора из ∆ A1 КО: ОА1 2 = ОК2 + А1К2, ОК= 25-16, ОК2 = 9, ОК =3. Дано: О1А = 5, АА1 = 15, АВ = 17. Найти: расстояние между ОО1 и АВ.
Задача №4 АО = 5 — дополнительное построение. AD = 2*(√25-9) = 2* √16 = 2*4 = 8. ABCD — прямоугольник. 4. SABCD = АВ • AD SABCD = 10 • 8 = 80. (Ответ: 80.) Найти: SABCD,
Задача №5 Дано: Sбок./Sосн. =1/2 Найти: H/2R Решение: 1. Sбок./Sосн = 2πRH/πR2 = 2H/R = ½. 2. 2H/R = ½. ═ H/2R = 1/8.
Задача № 6 Дано: ABCD — осевое сечение. Найти: Sбок./SABCD Решение: 1. Sбок.= 2πRH, ABCD — прямоугольник. 2. SABCD = AD • АВ, SABCD = 2R * Н. 3. Sбок./SABCD = = 2πRH/2RH = π (Ответ: π.).
Физкультминутка Мы с вами хорошо поработали, повторили всё необходимое. Прежде чем выполнить самостоятельную работу проведём физкультминутку. Сядьте удобнее, расслабьтесь. Каждое задание выполняем по 10 раз. Обведите верхнее основание цилиндра глазами по часовой стрелке, а нижнее – против часовой стрелки. Проведите глазами по оси цилиндра сверху вниз. Проведите глазами по диаметру справа налево. Закройте глаза. Откройте глаза. С новыми силами приступаем к работе.
Разноуровневая самостоятельная работа
1уровень Вариант I 1. Радиус цилиндра равен 10 см. Сечение, параллельное оси цилиндра и удаленное от нее на 8 см, имеет форму квадрата. Найти площадь сечения. 2. Диагональ осевого сечения цилиндра равна 8 √2 дм и образует с плоскостью основания цилиндра угол 45°. Найдите площадь полной поверхности цилиндра. Вариант II 1. Высота цилиндра равна 16 см. На расстоянии 6 см от оси цилиндра проведено сечение, параллельное оси цилиндра и имеющее форму квадрата. Найдите радиус цилиндра. 2. Диагональ осевого сечения цилиндра равна 8 дм и составляет с образующей угол 60°. Найдите площадь полной поверхности цилиндра. II уровень Вариант I 1. Прямоугольник вращается вокруг одной из своих сторон, равной 5 см. Площадь боковой поверхности цилиндра, полученного при вращении, равна 100π см2. Найдите площадь прямоугольника. 2. Хорда нижнего основания цилиндра отсекает от окружности основания дугу в 120°. Отрезок, соединяющий центр верхнего основания с серединой данной хорды, равен 4√2 см и образует с плоскостью основания угол 45°. Найдите площадь осевого сечения цилиндра. Вариант II 1. Прямоугольник, одна из сторон которого равна 5 см, вращается вокруг неизвестной стороны. Найдите площадь прямоугольника, если площадь боковой поверхности цилиндра, полученного при вращении, равна 60π см2. 2. Хорда нижнего основания цилиндра удалена от центра нижнего основания на 2√3 см и отсекает от окружности основания дугу в 60°. Отрезок, соединяющий центр верхнего основания с одним из концов данной хорды, образует с осью цилиндра угол 45°. Найдите площадь осевого сечения цилиндра.
Читайте также: Чем отмыть цилиндры мотоцикла
Подведение итогов урока на уроке было интересно и все понятно на уроке было интересно, но возникли затруднения на уроке было все понятно, но неинтересно на уроке ничего не заинтересовало на уроке было все непонятно и неинтересно
Домашнее задание П. 53, 54. 1 уровень — № 527, 531. II уровень — № 531, 544. III уровень — № 544, 601.
Видео:Видеоурок по математике "Цилиндр"Скачать

Геометрия сборник с решениями (стр. 3 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 |
Теперь нужно расписать как найти каждую из них.
В правильной треугольной пирамиде отрезок, соединяющий основание высоты пирамиды с серединой апофемы, равен m и образует с высотой пирамиды, угол β. Найдите полную поверхность пирамиды.
На рисунке изображена пирамида ACBO, OM-высота, OK-Апофема.
Точка L середина апофемы OK, LM образует с высотой OM угол β.
ΔOMK прямоугольный, следовательно ML является медианой этого треугольника, значит OL = LM = LK = m
ΔOLM равнобедренный, следовательно ∠OML = ∠LOM, а это значит что апофема образует с высотой угол β (на рисунке показано).
Sбок=p•a/2; где p — полупериметр основания, a — апофема OK.
В основании нашей пирамиды лежит правильный треугольник, стороны которого равны. Найдем сторону основания, для этого воспользуемся уже имеющимися данными. Как известно MK является радиусом вписанной в основание окружности.
Найдем чему равен r, зная что sinβ=MK/OK →OK=MK/sinβ=2m/sinβ
Цилиндр катится по некоторой плоскости. Какую фигуру образует при этом ось цилиндра?
Плоскость! А точнее прямоугольник!
Высота цилиндра 8см, диаметр основания 10см. Найдите площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4см от нее.
Итак на рисунке я показал сечение ABCD, параллельное оси. OK=4 см. OA=OB=Rокр=5
Площадь сечения равна AB*BC, где BC=H=8 см.
Остается найти AB, которая является основанием равнобедренного треугольника с высотой OK.
Радиус цилиндра r,а высота h.Найдите площадь осевого сечения цилиндра плоскостью,⊥ к основанию и отсекающей от окружности основания дугу в 60 градусов.
Даже рисунок практически не менял! Вот цилиндр, дуга AB равна 60 градусов. Линия AB является хордой стягивающей дугу AB. Она равна:
m=2R•sin(α/2), где α-угол образующий дугу.
Значит площадь сечения ABCD=R*H
Осевое сечение цилиндра − квадрат, площадь которого Q. Найдите площадь основания цилиндра.
Как найти площадь бок. поверхности правильной треугольной пирамиды, если сторона основания = 2см, а двугранные углы по 60 градусов?
Если двугранные углы по 60 градусов, то это значит что BC=SC=SB, а это значит что боковую поверхность образуют три равносторонних треугольника.
Угол M при основании трапеции MKPT равен 45o, MK=6√2, MT=10, KP=4. Найдите сумму квадратов диагоналей трапеции.
Решается довольно таки просто! Нарисуем рисунок, чтобы наглядно было понятно.
KD — высота. Так как угол M равен 45o, ∠MKD=180-90-45=45o, а это значит что MD=KD.
ΔMKD прямоугольный, а значит стороны относятся по теореме Пифагора как:
Теперь зная что MT=10, найдем DT=10-6=4.
А это значит что наша трапеция будет прямоугольной, т. е. одна из боковых сторон PT ⊥ MT
Найдем сначала диагональ KT, как видишь это просто зная что KD=PT=6
Теперь найдем диагональ MP, которая также находится по теореме Пифагора.
Найти нужно сумму квадратов диагоналей трапеции:
Найдите периметр ромба с наибольшей площадью если сумма длин его диагоналей равна 10.
Sр=d1*d2/2; где d1,d2 — диагонали ромба.
А теперь, маленький секрет! Когда будет произведение чисел больше, если в сумме они составляют n.
Ответ простой, когда каждое из них будет равно n/2.
Мы нашли площадь, хотя нам этого и не требовалось. Теперь нам нужен его периметр!
Читайте также: В цилиндр попал кусок резинки
Всего у ромба 4 стороны, значит P=4*2,5*√2=10√2
Основание пирамиды — правильный треугольник со стороной а. 2 боковые грани пирамиды перпендикулярны плоскости основания, а третья наклонена к ней под углом α. Найдите площадь полной поверхности пирамиды, как тут вообще решать, если нет никаких числовых данных?
ABC — основание пирамиды ABCS, BD — высота в равностороннем ΔABC. SD — опофема одной из боковых сторон.
Площадь пирамиды равна площади основания ABC плюс площади боковых сторон.
BD2=BC2-DC2 (Это по теореме Пифагора)
Теперь для того чтобы найти площадь боковой поверхности, внимательно рассмотрим все ее составляющие.
ΔSAC можно найти по формуле: SD*AC=SD*a
Решаем по теореме синусов:
sin(90-α) по формулам приведения равен cosα
Осталось найти площади ΔSBC, ΔSBA которые равны между собой так как имеют одинаковые стороны при основании и общее ребро SB. Эти треугольники также прямоугольные, так как перпендикулярны плоскости основания.
Площадь осевого сечения цилиндра равна 8 м^2,площадь основания -12м^2.Вычислите площ. сеч., параллельного оси и отстоящего от нее на 1 м.
Итак у нас имеется цилиндр, у которого площадь основания равна 12 м2, так как основание цилиндра составляют две окружности, найдем ее радиус зная что площадь каждой окружности равна 6 м2.
Теперь зная площадь осевого сечения ABCD можно найти высоту OO1, зная что Sос. сеч=H*2R
Мы уже решали с тобой задачу на нахождение площади плоскости. находящейся на расстоянии от осевого сечения, вспомни там мы сначала нашли сторону ML, а затем умножили на высоту. Для этого мы пользовались теоремой Пифагора:
Отрезок одним из своих концов скользит по окружности, оставаясь перпендикулярным к ее плоскости. Какая фигура при этом получится? Ответ : Цилиндрическая поверхность. Но как это доказать
Отрезок имеет начало и имеет конец. То есть он имеет длину равную h. Если такой отрезок будет скользить по окружности одним из концов получится цилиндр, так как он является перпендикулярным к плоскости окружности это будет прямой цилиндр. А сам отрезок будет являться образующей этого цилиндра.
В равностороннем цилиндре точка окружности верхнего основания соединена с одной из точек окружности нижнего основания. Угол между радиусами, проведёнными в эти точки, равен 30°. Определить угол между проведённой прямой и осью цилиндра.
Очень просто, для того чтобы понять достаточно одного рисунка.
Так как можно рассматривать отрезок AB как вектор, то так как между высотой и радиусом основания лежит угол 90 градусов, поэтому по сумме углов треугольника 180-90-30=60 градусов.
Периметры двух подобных четырехугольников относятся как 2:3.Найдите отношение их площадей
Периметры подобных фигур относятся как P1/P2=k
Найдите длину высоты прямоугольного треугольника, опущенной из вершины прямого угла, если она делит гипотенузу на отрезка, равные 3 и 27 см
Составьте уравнение, обозначить нужно высоту за x.
Значит площадь прямоугольного треугольника равна: (3+27)*X=30X, по правилу высота умноженная на прилежащую сторону.
Также площадь найти можно умножив катеты AB и BC и разделить на 2.
Так как высота BD образует новые прямоугольные треугольники ADB и BDC, то их длина найдется по теореме Пифагора.
Остается только подставить:
В конус вписан шар объемом 4/3п см в кубе. Найдите объем конуса, если его высота=3 см
шар объемом 4/3п вписан в конус, то есть радиус этого шара равен радиусу основания конуса.
Стороны основания правильной треугольной пирамиды а, боковое ребро b, определите высоту пирамиды.
Если пирамида правильная в основании лежит треугольник с равными сторонами. Чтобы найти высоту OO1 нужно найти AO1, которая согласно правилу равна радиусу описанной вокруг треугольника окружности.
📸 Видео
Объём цилиндраСкачать

11 класс, 32 урок, Объем цилиндраСкачать

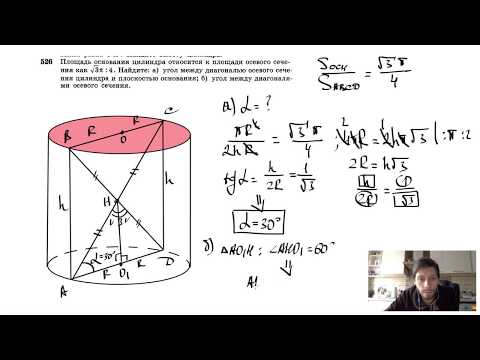
№526. Площадь основания цилиндра относится к площади осевого сечения как √3π:4. Найдите:Скачать
11 класс, 15 урок, Площадь поверхности цилиндраСкачать

РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

60. Площадь поверхности цилиндраСкачать

ЦИЛИНДР. КОНУС. ШАР.Скачать

Задачи на цилиндр. Объем цилиндра - bezbotvyСкачать

Длина окружности. Площадь круга - математика 6 классСкачать

Как запомнить площадь поверхности цилиндра #математикапрофиль #геометрияегэСкачать

КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

Длина окружности. Площадь круга. 6 класс.Скачать

ЦИЛИНДР геометрия егэ по математике профильный уровень ЯщенкоСкачать

Нахождение площади боковой поверхности цилиндраСкачать

ЗАДАЧА 769. МАТЕМАТИКА 6 класс. Площадь боковой поверхности цилиндра. ПРОЕКТ Домашнее обучение.Скачать

11 класс. Геометрия. Объем конуса. 21.04.2020Скачать








