2016-12-11
Найти электрическое давление, которое испытывает поверхность равномерно заряженной сферы радиуса $R$. Заряд сферы $Q$.
Первый вариант решения основан на законе сохранения энергии. Для удобства расчета представим себе, что сфера выполнена из абсолютно эластичного (неупругого) материала, а электрическое давление уравновешивается, например, давлением окружающего газа (внутри сферы газ отсутствует). Пусть в результате медленного и очень малого уменьшения давления газа радиус сферы увеличился на малую величину $\Delta R ( \Delta R \ll R)$. При этом над газом совершена работа:
$A = P \Delta V = P 4 \pi R^ \Delta R$, (1)
где $\Delta V = 4 \pi R^ \Delta R$ — изменение объема газа.
Работа над газом совершена за счет уменьшения электростатической энергии сферы:
Согласно закону сохранения энергии:
Величину $\Delta W$ можно было найти также, воспользовавшись выражением для энергии электрического поля. Действительно, после расширения сферы объем, занимаемый электрическим полем, уменьшился на величину шарового слоя толщиной $\Delta R: \Delta V = 4 \pi R^ \Delta R$. Электрическое поле до расширения в этом слое $E = \frac >$, учитывая малость $\Delta R$, можно считать однородным, а после расширения $E = 0$. Отсюда находим:
Второй вариант решения задачи основан на прямом расчете давления.
Рассмотрим малую площадку $\Delta S_$ на поверхности сферы, поверхностная плотность зарядов которой:
Давление $P$, испытываемое площадкой, по определению, равно:
где $F$ — сила, действующая со стороны зарядов сферы на заряд $\Delta Q = \sigma \Delta S$ площадки:
$F = E \cdot \Delta Q = E \sigma \Delta S$. (7)
Напряженность электрического поля $E$, создаваемая всеми зарядами сферы за исключением заряда $\Delta Q$, найдем из следующих соображений. Рассмотрим две близкие к поверхности сферы точки А и В: одна внутри сферы, другая — снаружи. Воспользуемся принципом суперпозиции для вычисления поля в точке В:
$E_ = E + 2 \pi k \sigma = \frac >$, (8)
Читайте также: 5557я 1609005 цилиндр пневматический пневмоусилитель сцепления урал
где $2 \pi k \sigma$ — поле, создаваемое зарядом $\Delta Q$ в точке В. Аналогично, для поля в точке А:
После несложных вычислений получаем, как и прежде:
Видео:Электростатика | электрическое поле бесконечной нити (тонкого цилиндра)Скачать
Давление электрического поля в цилиндре
Электрическое поле обладает энергией с плотностью $w=\frac \cdot \vec )> $. Поэтому полная энергия $W$ системы зарядов может быть выражена в виде интеграла по бесконечному объему: $$ \begin W=\int w(\vec )dV=\int \frac \cdot \vec )> dV \end $$ Если учесть, что $\vec =-\nabla \varphi$, то $$ W=-\int \frac )> dV $$ Применим к подынтегральному выражению тождество из векторного анализа: $$ (\nabla \varphi\cdot \vec )=\Div (\varphi \vec )-\varphi \Div \vec . $$ Тогда получим $$ W=-\frac \int \Div (\varphi \vec )dV + \frac \int \varphi \Div \vec dV= -\frac \oiint \varphi \vec d\vec +\frac \int \varphi \cdot 4\pi \rho dV, $$ где интеграл по объему преобразован в интеграл по поверхности в силу теоремы Гаусса-Остроградского.
Для ограниченных заряженных систем $D\lesssim \frac $, а $\varphi\lesssim \frac $. Поэтому при $r \rightarrow \infty$ интеграл по поверхности стремится к нулю: $$ \oiint \varphi \vec d\vec \lesssim \frac \rightarrow 0. $$ Получаем еще одно выражение для энергии системы зарядов: $$ \begin W=0 + \frac \int \varphi \cdot 4\pi \rho dV=\frac \int \varphi \rho dV= \frac \int \varphi dq. \end $$ В выражении (2) бесконечная область интегрирования сводится к ограниченному объему, в котором распределен заряд. Если заряд распределен по поверхности или вдоль линии, то $dq=\sigma dS$ или $dq=\varkappa dl$ соответственно.
Если электрическое поле по разные стороны от некоторой поверхности имеет нормальные компоненты $E_ ,\, D_ $ и $E_ ,\, D_ $ соответственно, то на данную поверхность действует давление $$ P=\frac D_ -E_ D_ > . $$ Давление направлено в сторону большего по абсолютной величине поля, независимо от направления поля.
Видео:Поле равномерно заряженного цилиндраСкачать
Давление электрического поля в цилиндре
Продемонстрируем возможности теоремы Остроградского-Гаусса на нескольких примерах.
Читайте также: Не работают два цилиндра ваз 2115 8 клапанов
Поле бесконечной однородно заряженной плоскости
Поверхностная плотность заряда на произвольной плоскости площадью S определяется по формуле:
где d q – заряд, сосредоточенный на площади d S; d S – физически бесконечно малый участок поверхности.
Пусть σ во всех точках плоскости S одинакова. Заряд q – положительный. Напряженность во всех точках будет иметь направление, перпендикулярное плоскости S (рис. 2.11).
Очевидно, что в симметричных, относительно плоскости точках, напряженность будетодинакова по величине и противоположна по направлению.
Представим себе цилиндр с образующими, перпендикулярными плоскости, и основаниями ΔS, расположенными симметрично относительно плоскости (рис. 2.12).
 | |
| Рис. 2.11 | Рис. 2.12 |
Применим теорему Остроградского-Гаусса. Поток ФЕ через боковую часть поверхности цилиндра равен нулю, т.к . Дляоснования цилиндра
Суммарный поток через замкнутую поверхность (цилиндр) будет равен:
Внутри поверхности заключен заряд . Следовательно, из теоремы Остроградского–Гаусса получим:
откуда видно, что напряженность поля плоскости S равна:
Полученный результат не зависит от длины цилиндра. Это значит, что на любом расстоянии от плоскости
Поле двух равномерно заряженных плоскостей
Пусть две бесконечные плоскости заряжены разноименными зарядами с одинаковой по величине плотностью σ (рис. 2.13).
Результирующее поле, как было сказано выше, находится как суперпозиция полей, создаваемых каждой из плоскостей .
Вне плоскостей напряженность поля
Полученный результат справедлив и для плоскостей конечных размеров, если расстояние между плоскостями гораздо меньше линейных размеров плоскостей (плоский конденсатор).
Между пластинами конденсатора действует сила взаимного притяжения (на единицу площади пластин):
Механические силы, действующие между заряженными телами, называют пондермоторными.
Тогда сила притяжения между пластинами конденсатора:
где S – площадь обкладок конденсатора. Т.к. , то
Это формула для расчета пондермоторной силы.
Поле заряженного бесконечно длинного цилиндра (нити)
Пусть поле создается бесконечной цилиндрической поверхностью радиуса R, заряженной с постоянной линейной плотностью , где d q – заряд, сосредоточенный на отрезке цилиндра (рис. 2.14).
Из соображения симметрии следует, что Е в любой точке будет направлена вдоль радиуса, перпендикулярно оси цилиндра.
Читайте также: Порядок работы цилиндров ямз 236 без турбины схема
Представим вокруг цилиндра (нити) коаксиальную замкнутую поверхность (цилиндр в цилиндре) радиуса r и длиной l (основания цилиндров перпендикулярно оси). Для оснований цилиндров для боковой поверхности т.е. зависит от расстояния r.
Следовательно, поток вектора через рассматриваемую поверхность, равен
При на поверхности будет заряд По теореме Остроградского-Гаусса , отсюда
Если , т.к. внутри замкнутой поверхности зарядов нет (рис.2.15).
Если уменьшать радиус цилиндра R (при ), то можно вблизи поверхности получить поле с очень большой напряженностью и, при , получить нить.
Поле двух коаксиальных цилиндров с одинаковой линейной плотностью λ, но разным знаком
Внутри меньшего и вне большего цилиндров поле будет отсутствовать (рис. 2.16) .
В зазоре между цилиндрами, поле определяется так же, как и в предыдущем случае:
Это справедливо и для бесконечно длинного цилиндра, и для цилиндров конечной длины, если зазор между цилиндрами намного меньше длины цилиндров (цилиндрический конденсатор).
Поле заряженного пустотелого шара
Пустотелый шар (или сфера) радиуса R заряжен положительным зарядом с поверхностной плотностью σ. Поле в данном случае будет центрально симметричным, – в любой точке проходит через центр шара. ,и силовые линии перпендикулярны поверхности в любой точке. Вообразим вокруг шара – сферу радиуса r (рис. 2.17).
Если то внутрь воображаемой сферы попадет весь заряд q, распределенный по сфере, тогда
Внутри сферы, при поле будет равно нулю, т.к. там нет зарядов:
Как видно из (2.5.7) вне сферы поле тождественно полю точечного заряда той же величины, помещенному в центр сферы.
Поле объемного заряженного шара
Для поля вне шара радиусом R (рис. 2.18) получается тот же результат, что и для пустотелой сферы, т.е. справедлива формула:
Но внутри шара при сферическая поверхность будет содержать в себе заряд, равный
где ρ – объемная плотность заряда, равная: ; – объем шара. Тогда по теореме Остроградского-Гаусса запишем:
Таким образом, внутри шара
📸 Видео
ЧК_МИФ_ФМЛ_30 _ 3_1_4_7 (L2) ПОЛЕ РАВНОМЕРНО ЗАРЯЖЕННОГО ЦИЛИНДРАСкачать
Теорема Гаусса для расчета полей цилиндра (нити) и плоскостиСкачать
Применение теоремы Гаусса-Остроградского. Напряжённость поля пластины, сферы и шара.Скачать
Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать
Урок 47 (осн). Расчет давления жидкости на дно и стенки сосудаСкачать
Электромагнетизм Пр3.4. Теорема Гаусса. Поле бесконечного цилиндра.Скачать
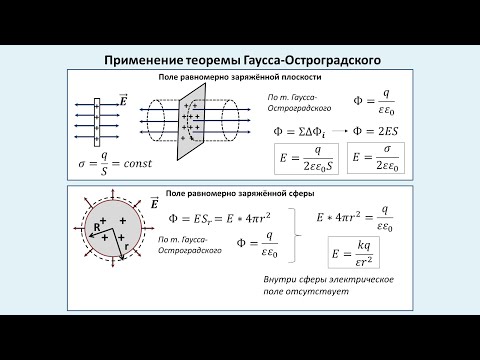
Билет №02 "Теорема Гаусса"Скачать
Что такое датчик давления ?Скачать
ДАВЛЕНИЕ ЖИДКОСТИ на дно и стенки сосуда 7 класс физика формулаСкачать
Урок 46 (осн). Передача давления жидкостями и газами. Закон ПаскаляСкачать
Урок 218. Напряженность электрического поляСкачать
Электростатика | электрическое поле бесконечной плоскостиСкачать
Урок 44 (осн). Задачи на вычисление давленияСкачать
Один моль аргона, находящийся в цилиндре при температуре T1 =600 K и давлении p1 =4⋅10^5 - №29414Скачать
ЧК МИФ ЛЭТИ_ 3_1_1_4_( L3) Применение теоремы Гаусса: поля цилдиндра и бесконечного слояСкачать
43. Применение теоремы ГауссаСкачать
Парадокс сужающейся трубыСкачать
Урок 224. Напряженность поля неточечных зарядовСкачать
