Диаметр основания цилиндра формулы (7 видео)

Содержание

Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников
Диаметр и высота цилиндра
Свойства
Диаметр и диагональ цилиндра
Свойства
Геометрические тела. Цилиндр.
Формулы нахождения элементов цилиндра.
Что такое цилиндр: определение, элементы, виды, варианты сечения
Определение цилиндра
Основные элементы цилиндра
Геометрические тела. Цилиндр.
Формулы нахождения элементов цилиндра.
Высота и площадь основания цилиндра
Свойства
📸 Видео

Видео:Видеоурок по математике "Цилиндр"Скачать

Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников

Курс-тренинг Разбираем вариант 97 (1-14) —> Полный цикл видеоуроков по задачам 1-14 —> Полная В-подготовка (задачи 1-14) Полный цикл видеоуроков по задачам 1-14 При каком условии верно равенство 2990 + 1990 + 990 = 3900? —> Новые курсы: «EGE-мастер», «Достойный балл», «Ларинские варианты», «Раз-в-неделю», «Всё включено» —> Постоянно работают курсы для выпускников, учителей и репетиторов

12(B13). Найти диаметр основания цилиндра, если дана боковая поверхность (вар. 49)

Площадь боковой поверхности цилиндра равна 56π, а высота равна 7. Найдите диаметр основания.

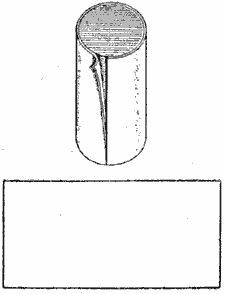
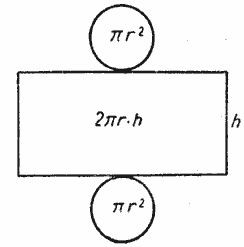
Что представляет из себя боковая поверхность цилиндра? Разрежем его мысленно по образующей. При этом получим обыкновенный прямоугольник. Одно из его измерений — высота цилиндра. Второе измерение — длина окружности основания цилиндра. Она равна 2π·R = π·(2R) = π·D. На рисунке изображена полная развёртка цилиндра, но нас интересует только прямоугольник. Площадь прямоугольника (боковая поверхность) равна (π·D)·Н. По условию она равна 56π. Получаем (π·D)·Н = 56π. Отсюда D·Н = 56. Учтём теперь, что по условию высота равна 7. D·7 = 56. Отсюда находим диаметр D = 8. Ответ: 8 Можно поступить и так. В формулу боковой поверхности цилиндра S_бок. = 2π·R·H подставить площадь 56π и высоту 7, получим 56π = 2πR·7, 56 = 2R·7, 8 = 2R = D.

Автор: Ольга Себедаш Просмотров: 45065

Комментарии к этой задаче:

Комментарий добавил(а): Артур
Дата: 2014-06-03

А общее формула нахождение диаметра цилиндра? Она имеет лишь такое произведение? Или есть иное?

Видео:№537. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длинеСкачать

Диаметр и высота цилиндра

Видео:Цилиндр - расчёт площади, объёма.Скачать

Свойства

Через диаметр цилиндра можно рассчитать его радиус и периметр основания цилиндра. Радиус будет равен половине диаметра, а периметр – его произведению на число π. r=D/2 P=πD

Зная диаметр и высоту цилиндра, можно узнать площадь, объем, диагональ цилиндра и остальные параметры. Площадь боковой поверхности цилиндра представляет собой площадь прямоугольника, сторонами которого являются периметр основания цилиндра и его высота. Чтобы затем найти площадь полной поверхности цилиндра через диаметр и высоту, нужно к площади боковой поверхности добавить площадь верхнего и нижнего оснований, каждое из которых равно произведению числа π на четверть квадрата диаметра. S_(б.п.)=hP=πDh S_(п.п.)=S_(б.п.)+2S_(осн.)=πDh+(πD^2)/2=πD/2(2h+D) P=πD

Читайте также: Фрезеровка блока цилиндров змз 402

Объем цилиндра представляет собой площадь его основания, умноженную на высоту. Чтобы найти объем цилиндра через диаметр и высоту, нужно умножить квадрат диаметра на четверть числа π и на высоту. V=(πD^2 h)/4 P=πD

Диагональ цилиндра находится из прямоугольного треугольника, в котором она является гипотенузой, а катеты представлены высотой и диаметром цилиндра. По теореме Пифагора диагональ цилиндра через высоту и диаметр цилиндра равна квадратному корню из суммы их квадратов. (рис. 25.1) d=√(h^2+D^2 ) P=πD

Чтобы найти радиус сферы вписанной в цилиндр, если его диаметр равен высоте, нужно разделить диаметр цилиндра либо высоту на два, так как радиус вписанной сферы равен радиусу цилиндра. (рис.25.2) r_1=h/2=D/2 P=πD

Радиус сферы, описанной вокруг цилиндра, при соблюдении тех же условий (равенство диаметра цилиндра и его высоты) равен половине диагонали цилиндра.(рис.25.3) R=d/2=√(h^2+D^2 )/2

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Диаметр и диагональ цилиндра

Видео:Цилиндр, конус, шар, 6 классСкачать

Свойства

Зная диаметр цилиндра, можно вычислить радиус цилиндра и периметр окружности цилиндра, которая представляет собой его основание. Радиус будет равен одной второй диаметра, а периметр окружности – произведению диаметра на число π. r=D/2 P=πD

Первое, что можно вычислить через диаметр и диагональ цилиндра – это его высота. Так как высота непосредственно связана со всеми остальными параметрами цилиндра, такими как площадь, объем и прочие, то она является необходимым звеном для геометрического калькулятора цилиндра. (рис.25.1) h=√(d^2-D^2 )

Площадь боковой поверхности цилиндра равна произведению высоты на длину окружности в основании цилиндра, таким образом, раскрывая эту формулу, получаем, что площадь боковой поверхности равна произведению числа π и диаметра на квадратный корень из разности квадратов диагонали и диаметра. S_(б.п.)=hP=πD√(d^2-D^2 )

Площадь полной поверхности цилиндра представлена площадью боковой поверхности в сумме с площадью двух оснований в виде окружностей. S_(п.п.)=S_(б.п.)+2S_(осн.)=πD(√(d^2-D^2 )+D)

Чтобы найти объем цилиндра через диаметр и диагональ нужно представить высоту цилиндра в виде квадратного корня разности из квадратов диагонали и диаметра, а затем умножить это на площадь основания, состоящую из числа π и четверти квадрата диаметра. V=(πD^2 h)/4=(πD^2 √(d^2-D^2 ))/4

Чтобы в цилиндр можно было вписать сферу, нужно чтобы диаметр цилиндра был равен его высоте, тогда сфера будет соприкасаться со всеми гранями цилиндра и ее радиус будет равен радиусу цилиндра, то есть половине его диаметра. (рис. 25.2) r_1=r=D/2

Чтобы вокруг цилиндра можно было описать сферу, нужно точно так же чтобы диаметр цилиндра совпадал с высотой, и радиус описанной сферы будет равен половине диагонали цилиндра. R=d/2

Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Геометрические тела. Цилиндр.

Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.

ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.

Цилиндрические сечения боковой поверхности кругового цилиндра.

Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.

Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.

Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.

Круговой цилиндр – цилиндр, основанием которого является круг.

Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.

Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.

Призма – это частный случай цилиндра.

Видео:ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ЦИЛИНДРА РАВНА 36п, А ДИАМЕТР ОСНОВАНИЯ РАВЕН 6. НАЙДИТЕ ВЫСОТУ ЦИЛИНДРАСкачать

Формулы нахождения элементов цилиндра.

Площадь боковой поверхности прямого кругового цилиндра:

Площадь полной поверхности прямого кругового цилиндра:

Объем прямого кругового цилиндра:

Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h₁ и максимальной высоты h₂.

Площадь боковой поверхности скошенного цилиндра:

Площадь оснований скошенного цилиндра:

Площадь полной поверхности скошенного цилиндра:

Объем скошенного цилиндра:

S_бок — площадь боковой поверхности;

Видео:Радиус основания цилиндра равен 26. Найти площадь сеченияСкачать

Что такое цилиндр: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Видео:11 класс, 32 урок, Объем цилиндраСкачать

Определение цилиндра

Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.

Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.

Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O₁O₂ на 180° или прямоугольников ABO₂O₁/O₁O₂CD вокруг стороны O₁O₂ на 360°.

Видео:11 класс. Геометрия. Объем цилиндраСкачать

Основные элементы цилиндра

Основания цилиндра – два одинаковых по размеру/площади круга с центрами в точках O₁ и O₂.
R – радиус оснований цилиндра, отрезки AD и BC – диаметры (d).
O₁O₂ – ось симметрии цилиндра, одновременно является его высотой (h).
l (AB, CD) – образующие цилиндра и одновременно с этим стороны прямоугольника ABCD. Равны высоте фигуры.

Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.

длина данного прямоугольника равна длине окружности основания цилиндра ( 2πR );
ширина равна высоте/образующей цилиндра.

Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.

Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

Геометрические тела. Цилиндр.

ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.

Цилиндрические сечения боковой поверхности кругового цилиндра.

Круговой цилиндр – цилиндр, основанием которого является круг.

Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.

Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.

Призма – это частный случай цилиндра.

Видео:Егэ.Длина окружности основания цилиндра равна 3 ,площадь боковой поверхности равна 6 .Найдите высотуСкачать

Формулы нахождения элементов цилиндра.

Площадь боковой поверхности прямого кругового цилиндра:

Площадь полной поверхности прямого кругового цилиндра:

Объем прямого кругового цилиндра:

Площадь боковой поверхности скошенного цилиндра:

Площадь оснований скошенного цилиндра:

Площадь полной поверхности скошенного цилиндра:

Объем скошенного цилиндра:

S_бок — площадь боковой поверхности;

Видео:Цилиндр. Определение, свойства, формулы.Скачать

Высота и площадь основания цилиндра

Видео:Объем цилиндра.Скачать

Свойства

Через площадь основания цилиндра можно найти диаметр цилиндра и радиус. Поскольку площадь окружности, которая представляет собой основание цилиндра, равна произведению квадрата радиуса или четверти квадрата диаметра на число π, то эти два параметра легко найти, составив отношение из нужного количества площадей к числу π, и извлечь затем из него квадратный корень. r=√(S/π) D=√(4S/π)=2√(S/π)

Также зная площадь основания цилиндра и высоту, можно сразу найти объем цилиндра, перемножив эти два показателя. V=S_(осн.) h

Периметр окружности, лежащей в основании цилиндра, через площадь основания равен двум квадратным корням из произведения площади основания на число π. P=2√Sπ

Площадь боковой поверхности цилиндра, зная высоту и площадь основания, можно найти, выразив радиус через площадь основания и умножив его на удвоенное число π и высоту, а площадь полной поверхности будет представлена как сумма этого значения и двух заданных площадей основания. S_(б.п.)=2h√Sπ S_(п.п.)=S_(б.п.)+2S_(осн.)=2h√Sπ++2S_(осн.)

Чтобы найти диагональ цилиндра через площадь основания и высоту, также понадобится извлечь из площади основания радиус, и затем подставив его в теорему Пифагора, найти диагональ, как гипотенузу полученного прямоугольного треугольника. (рис.25.1) d=√(D^2+h^2 )=√(4S/π+h^2 )

Радиусы вписанной и описанной вокруг цилиндра сфер равны радиусу цилиндра и половине диагонали соответственно. (рис. 25.2,25.3) r_1=r=√(S/π) R=d/2=√(4S/π+h^2 )/2