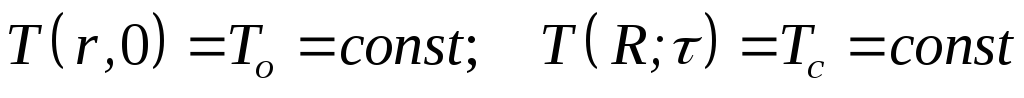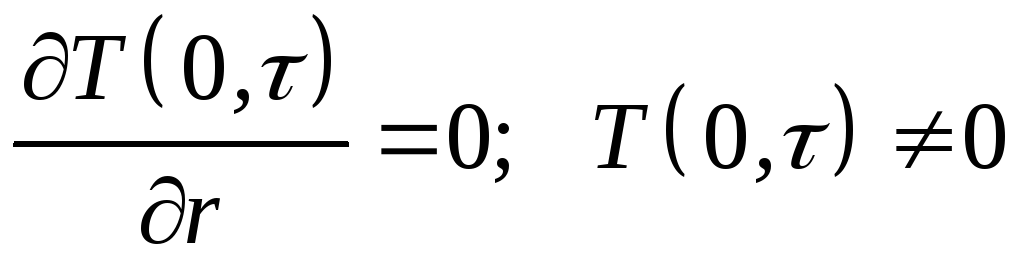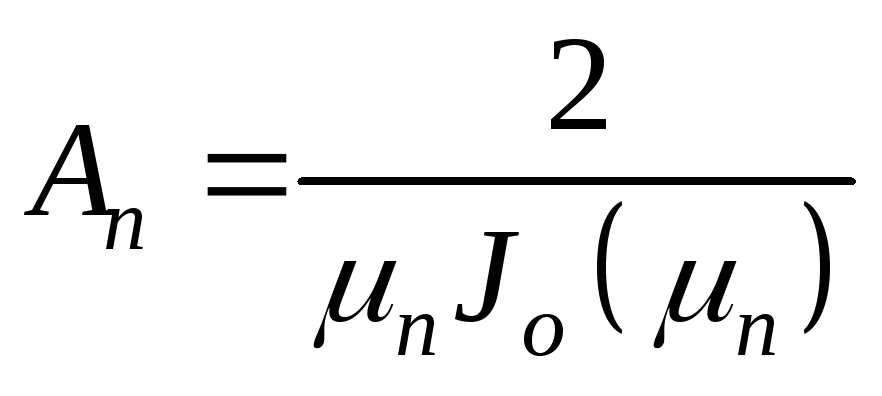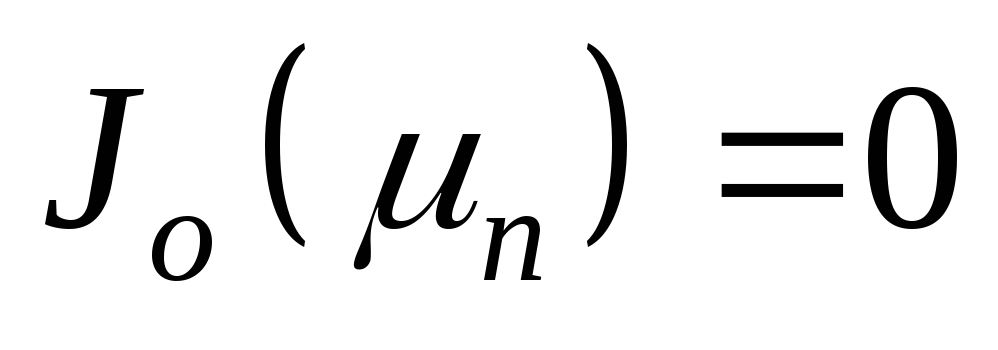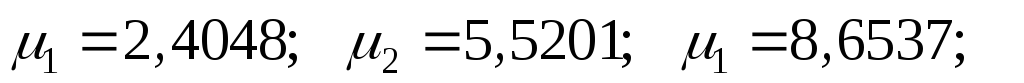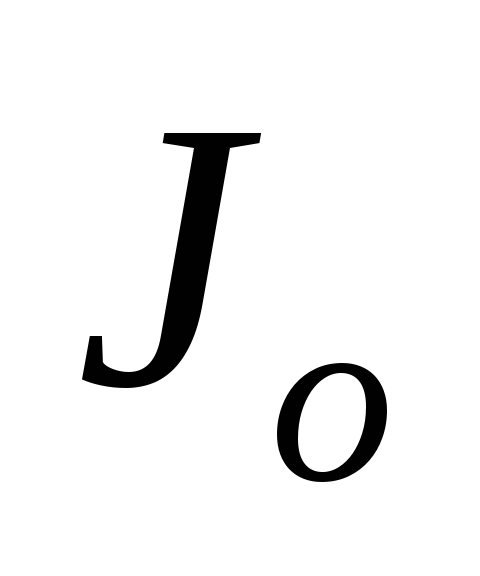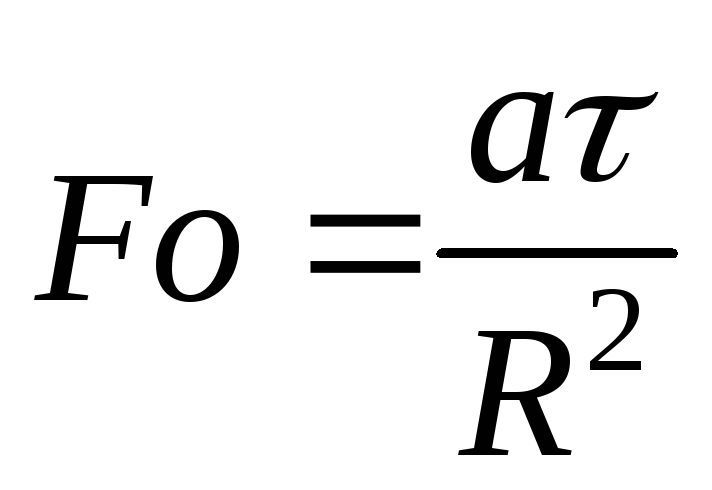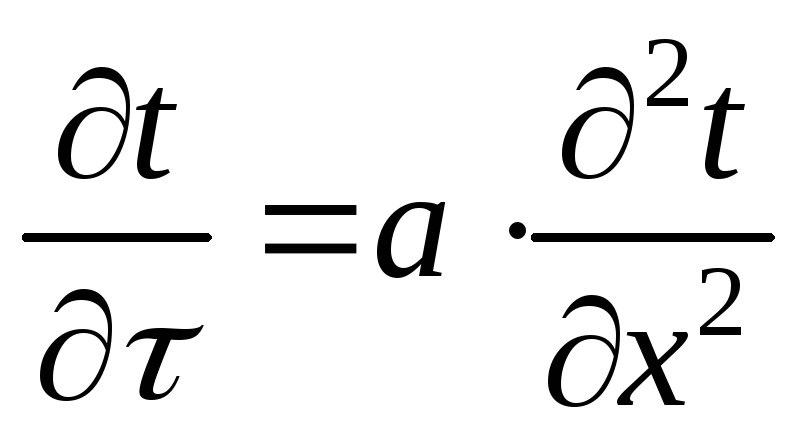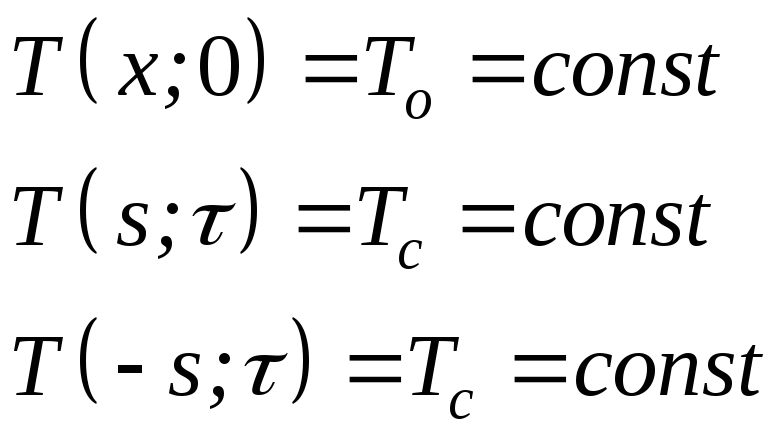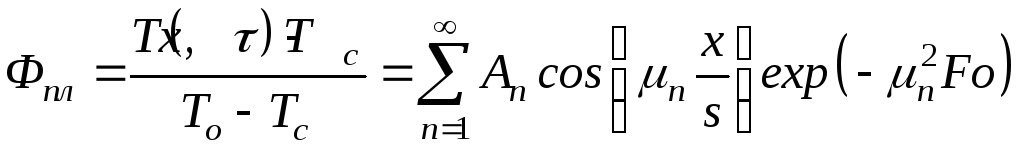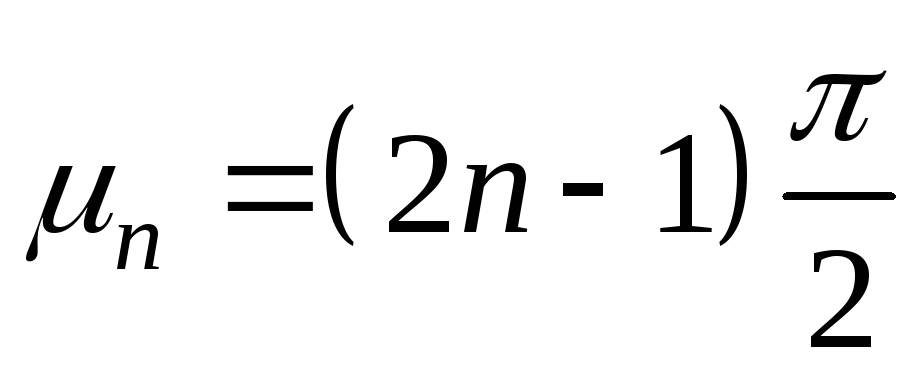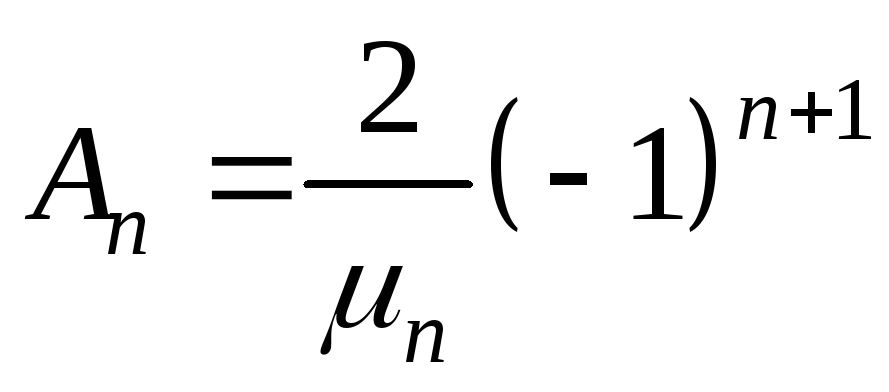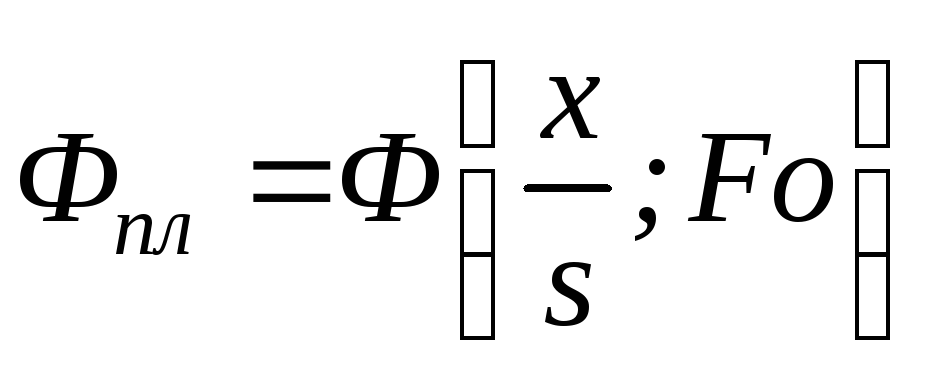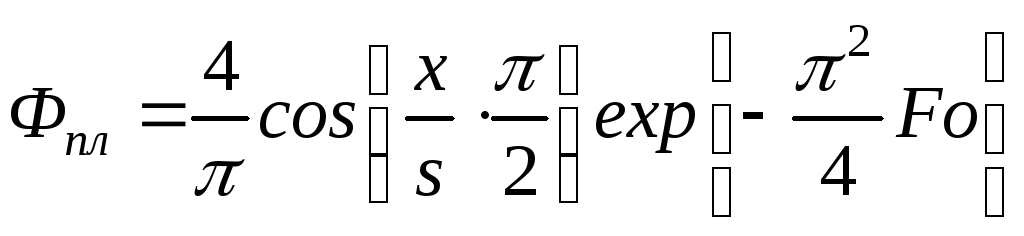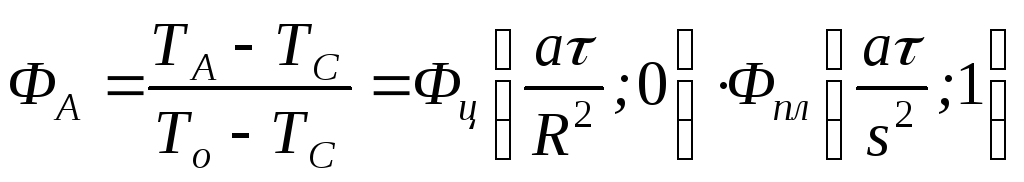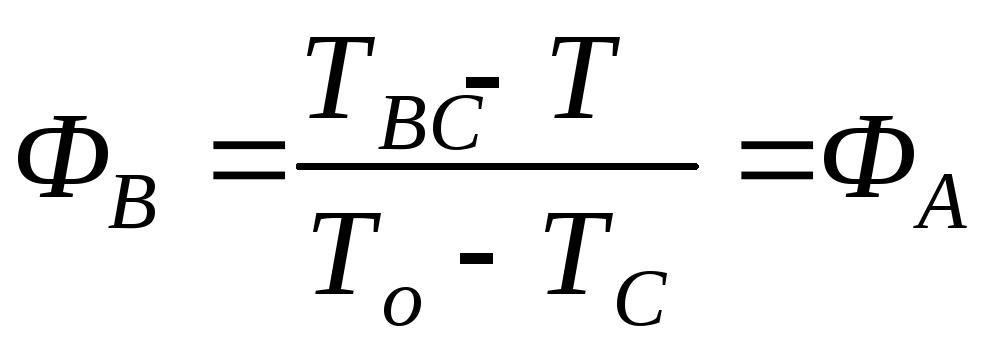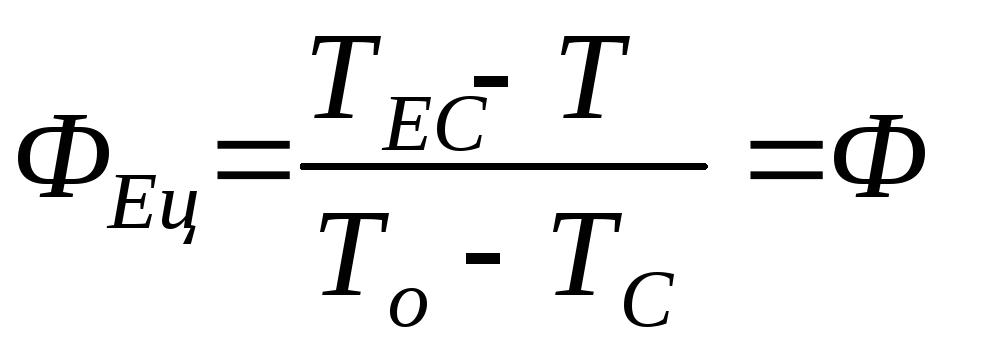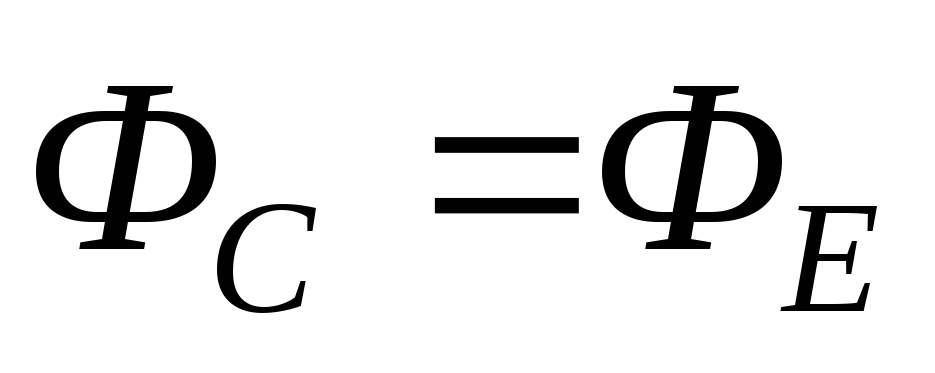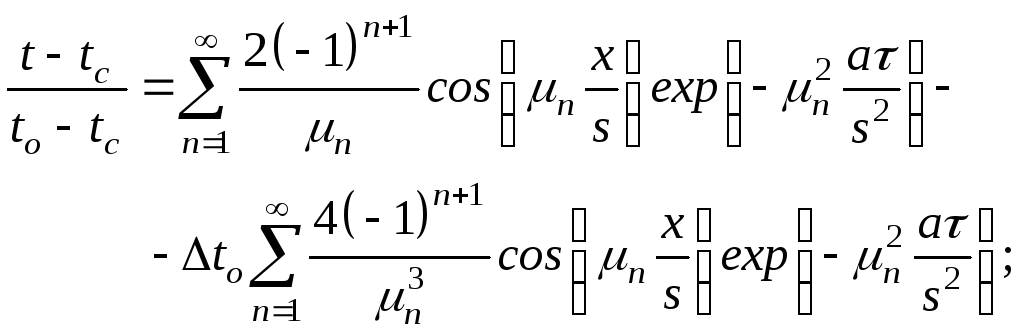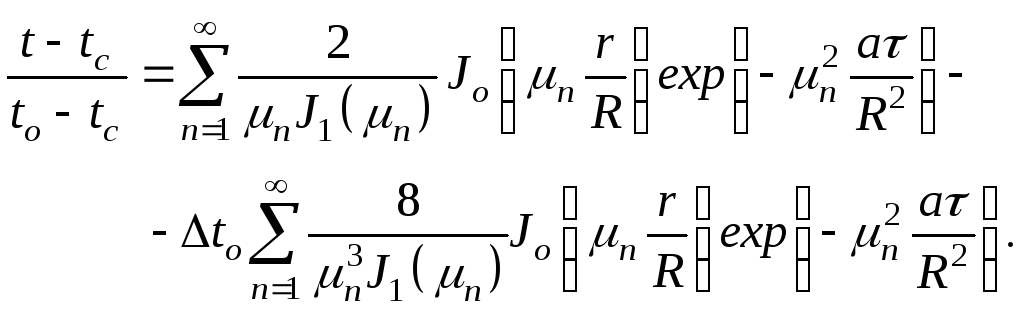Дифференциальное уравнение теплопроводности цилиндра (4 видео)

Видео:6-1. Уравнение теплопроводностиСкачать

2 Решение дифференциального уравнения теплопроводности для неограниченного цилиндра

Если длина l цилиндра значительно больше его диаметра 2R (l/2R > 3), то его можно уподобить неограниченному цилиндру, у которого длина бесконечно велика по сравнению с его диаметром.

Если теплообмен между поверхностью цилиндра и окружающими телами происходит одинаково по всей поверхности, то температура его будет зависеть только от времени и радиуса (симметричная задача), т.е. задача сводится к следующему:

Дан неограниченный цилиндр при некотором заданном радиальном распределении температур в виде функции Т_о = f(r). В начальный момент времени поверхность цилиндра мгновенно нагревается до некоторой температуры Т_с, которая поддерживается постоянной на протяжение всего процесса нагрева (охлаждения). Необходимо найти распределение температуры внутри цилиндра в любой момент времени.

Дифференциальное уравнение теплопроводности в данном случае имеет вид (1.2).

Решение задачи при краевых условиях

; (2.1)

(2.2)

(последнее из которых означает, что температура на оси цилиндра на протяжении всего процесса теплообмена должна быть конечной) имеет вид:

, (2.3)

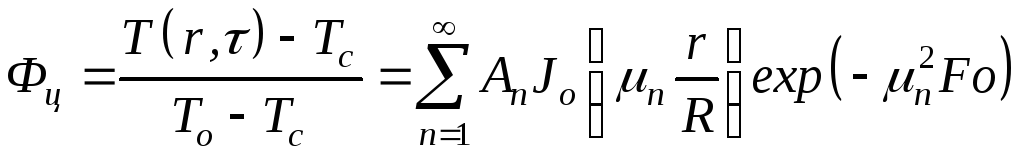
где

_n – корни характеристического уравнения :

— функция Бесселя первого рода нулевого порядка [1];

— число Фурье.

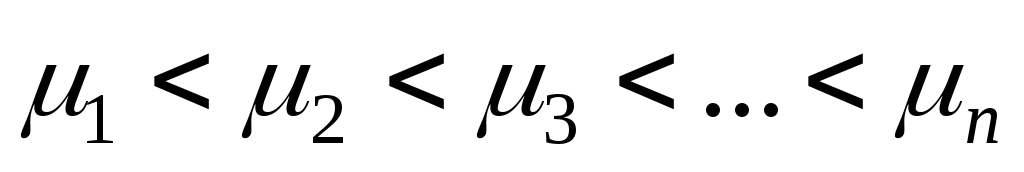
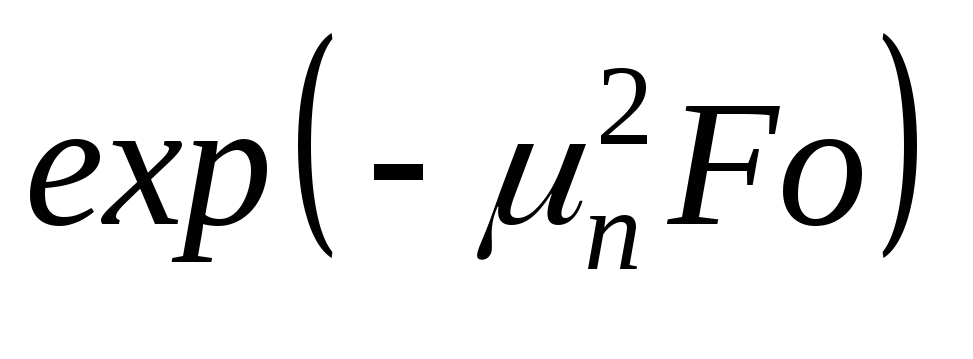
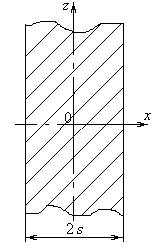
Из анализа решения (2.3) следует, что ряд быстро сходится, так как и с увеличением_n А_n уменьшается, а также резко уменьшается экспоненциальная функция . Поэтому, если исключить из рассмотрения малые значенияFo

Неограниченная пластина представляет собой тело, ограниченное двумя плоскостями.

Изменение температуры происходит только в одном направлении х, в двух других направлениях температура неизменна (одномерная задача) (рис. 2).

Условие задачи математически можно сформулировать в виде дифференциального уравнения со следующими краевыми условиями:

(3.1)

, (3.2)

где

т.е. относительная температура является функцией относительной координаты и числа Фурье

При малых числах Fo (Fo 0,3

. (3.4)

все функции, используемые в решениях (2.3)-(3.4) табулированы [1].

Зная решение дифференциального уравнения теплопроводности для бесконечного цилиндра и пластины (2.3)-(3.4), используя (2.1) можно получить решение для цилиндра конечной длины. Например, для определения температуры в точках, указанных на рис. 1, нужно записать уравнения:

;

и т.д.

На практике мы очень часто сталкиваемся с задачами, когда при постоянной температуре поверхности в теле уже имеется некоторое распределение температур. В случае отличия начального распределения температуры от равномерного, формулами (2.3)-(3.4) пользоваться нельзя. нужно пользоваться такими формулами:

Читайте также: Структурный состав осевого цилиндра корня

– для пластины бесконечной длины

(3.5)

– для цилиндра бесконечной длины

(3.6)

где t_о – разница между температурой центра и поверхности

образца в начальный момент времени;

J₁ – функция бесселя первого рода первого порядка [1]

решения (3.5) и (3.6) предполагают, что начальное распределение температуры описывается квадратичной параболой.

Отношение разности температур поверхности и центра тела в процессе нагрева t к начальной разности этих температур t_о называется степенью выравнивания температур  = t/t_о.

Степень выравнивания температур является функцией числа Фурье и для тел различной формы ее можно определить по графику (рис. 1, приложение Б).

Видео:Закон и уравнение теплопроводностиСкачать

Постановка задачи и вывод дифференциального уравнения теплопроводности для сплошного цилиндра. Аналитическое решение.

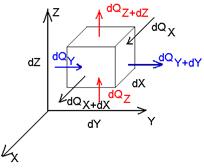
Дифференциальное уравнение теплопроводности выводится на основе закона сохранения энергии. Из всего рассматриваемого объема выделим элементарный объем dV и процесс будем рассматривать в течении элементарного промежутка времени.

· Тепло физические параметры среды постоянны

· Температурной деформацией пренебрегаем

· Внутренний источник тепла , если он есть, распределен по всему объему

dQ₁ – количество тепла подведенного к рассматриваемому объему dV за время dτ за счет процессов электропроводности

dQ₂ – количество тепловой энергии, которой выделяется на dV за dτ за счет действия внутреннего источника тепла

dQ – изменение внутренней энергии рассматриваемого объема за dτ (изменение энтальпии тела).

Ø Методы переноса тепла: теплопроводность, тепловая конвекция, излучение

Ø Конвективный обмен – возможен только в подвижных средах. Перенос осуществляется только за счет перемещение самого вещества.

Ø Тепловое излучение – перенос тепла происходит в 2 этапа. Сначала тепло преобразуется в тепловую энергию, а затем обратно.

Ø Теплопроводность – перенос тепла в твердых телах, жидкостях или газах, если жидкость и газы неподвижны.

Механизм данного явления объясняется на основании молекулярно — кинетических изменений. Перенос энергии осуществляется вследствие теплового движения и энергетического взаимодействия между микрочастицами (молекулами, атомами, электронами), из которых состоит данное тело.

Теплопроводность в чистом виде существует только в твердых телах. А в подвижных средах теплообмен осуществляется за счет теплопроводности, конвекции и излучения.

По теплопроводности тепло распространяется от нагретых участков к холодным, то есть в сторону убывания температуры.

Температура определяет степень нагретости тела.

Читайте также: Главный цилиндр сцепления даф 95 ати

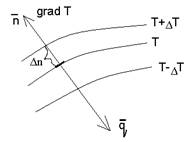
Процесс теплопроводности неразрывно связан с распределением температуры внутри тела, поэтому необходимо дать определение температурному полю и градиенту температуры:

— температурным полем называется совокупность значений температуры в каждой точке пространства в данный момент времени

Геометрическое место точек в пространстве имеющих одинаковую температуру, называется изотермической поверхностью

Поскольку любая точка пространства в данный момент времени может иметь только одно значение температуры, то изотермические поверхности не пересекаются →

— температурный градиент – предел отношения изменения температуры ΔТ к расстоянию между изотермами по нормали Δn.

Lim (ΔТ / Δn) _Δ_n→0 = = grad T. -единичный вектор

Является вектором, направленным по нормали к изотермической поверхности в сторону возрастания температуры его размерность [ 0 С/м]

Наибольшее изменение температуры может происходить по нормали к изотермическим поверхностям.

· Количества тепла, прошедшего через произвольную изотермическую поверхность за некоторый интервал времени τ – будем обозначать P [Вт]

· Количества тепла, прошедшего через произвольный изотермическую поверхность в единицу времени будем обозначать – тепловой поток Q [Дж].

· Тепловой поток отнесенный к единице поверхности, называется плотностью теплового потока – q [Вт/м 2 ]

· Закон Фурье (связь q и grad T). Фурье экспериментально установил что, количество переданного тепла пропорционально падению температуры, времени и площади сечения, перпендикулярного направлению распространению тепла

· λ – коэффициент теплопроводности – представляет собой количество тепла, которое роходит в единицу времени через один квадратный метр изотремической поверхности при температурном градиенте =1

В общем случаи λ зависит от температуры

· С – теплоемкость – количество энергии необходимого для нагрева 1 кг вещества на 1 градус. [Дж/кг 0 С]

dQ_X = q_X * dY * dZ * dτ

dQ₂ = q_V dV dτ, где q_V – количества тепла выделившегося в единице объема в единицу времени (внутренний источник тепла).

dQ = dU = ρ C dV dτ , где ρ – плотность среды [кг/м 3 ]

Из закона Фурье:

а – коэффициент температура проводность [м 2 / 0 С]

Постановка задачи:

1. рассматриваем сплошной цилиндр

3. цилиндрическая система координат

4. теплофизические свойства постоянны

5. внутреннего источника тепла нет (q_V =0)

Переходим от декартовой системы координат к цилиндрической:

Цилиндрические (Ц) и декартовые (Д) координаты связаны следующим образом:
Д ® Ц	Ц ® Д

Читайте также: Рабочий цилиндр сцепления ремонт или замена

Оператор Лапласа для цилиндрической системы координат запишется:

С учетом поставленной задачи получаем:

Охлаждение (нагревание) бесконечного длинного цилиндра.

Цилиндр радиусом г₀ отдает теплоту окружающей среде через свою боковую поверхность; коэффициент теплоотдачи α во всех точках поверхности одинаков и остается постоянным на протяжении всего периода охлаждения. Температура среды Tcp постоянна. В начальный момент времени при τ = 0 температура является некоторой функцией T (r, 0) = f (r). При этих условиях уравнение теплопроводности принимает вид:

Граничные и начальные условия:

· при τ = 0 и 0 0 и r = 0

· при τ > 0 и r = r₀

Сформулированную задачу решим с помощью разделения переменных, т. е.

(r, τ) = φ (τ) ψ (r).

Подставив это выражение в уравнение (*),получим два обыкновенных дифференциальных уравнения вида

Если обозначить kr₀ = μ , тогда частное решение уравнения (*) будет иметь вид:

где — коэффициент температуро-проводность

Постоянная μ определяется из граничных условий (r= r₀), решение которых приводит к характеристическому уравнению:

(2) где J₁, (μ) — функция Бесселя первого рода первого порядка.

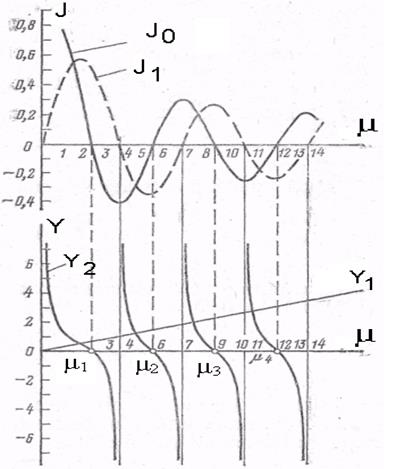
Уравнение (+) является трансцендентным, и его удобно решать графическим способом, обозначив:

· Отметим, что у₂ обращается в нуль в тех точках, для которых Jo (μ) = 0.

· В тех точках, в которых функция J₁ (μ₁) обращается в нуль, функция у₂ претерпевает разрыв непрерывности и становится равной ± оо.

Функции Jo (μ) и J₁ (μ) являются периодическими затухающими функциями.

— Кривая у₂ = напоминает котангенсоиду, но с убывающим периодом.

— Функция у₁ графически представляет прямую линию, проходящую через начало координат.

Выполнив построение, как показано на рис, в точках пересечения функции у₂ с прямой у₁ получим значения корней характеристического уравнения

Из рис следует, что уравнение (2) имеет бесчисленное множество решений, а сами корни, представляют ряд возрастающих чисел, т. е. μ₁ 100) прямая совпадает с осью абсцисс и корни характеристического уравнения не зависят от Bi, а определяются из условий

· Если рассматривать охлаждение цилиндра при условии Bi → 0

· Если Fo ≥ 0,25, при вычислении безразмерной температуры можно ограничиться первым членом ряда. Допускаемая при этом ошибка не превысит 1 %.

Дата добавления: 2016-04-19 ; просмотров: 2665 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ