Дифференциальный цилиндр оказывает большую силу при разжатии чем при сжатии (7 видео)

Содержание

Диаграмма сжатия. особенности разрушения при сжатии
Диаграмма сжатия. особенности разрушения при сжатии
Тема 2.2. Растяжение и сжатие
🎥 Видео

Видео:Как синхронизировать движение гидроцилиндров? Почему происходит перекос?Скачать

Диаграмма сжатия. особенности разрушения при сжатии

Видео:Гидроцилиндр - устройство и принцип работыСкачать

Диаграмма сжатия. особенности разрушения при сжатии

Схема сжатия. особенность Трещина при сжатии Диаграмма сжатия построена для изучения «поведения» материала при сжатии. Испытание на сжатие металла проводят на образце в форме цилиндра с высотой диаметра (обычно d = h == 20 мм, автоматическая

испытательная машина d-h == 6 мм). Для других материалов образец используется в форме история * Более точный способ определить истинную деформацию, например, В.А.Гетев В.Д. Эд в курсе «Сопротивление материала»

48 кубов (стороны куба равны: a = 50 мм Людмила Фирмаль

для дерева, 70 мм для цемента, 200 или 300 мм для бетона). Рассмотрим схему сжатия стали и чугуна. Для ясности нарисуйте эти материалы в одну фигуру с растянутой фигурой (рис. 44) .В первом квартале показана диаграмма растяжения и одного сжатия. В начале загрузки низкоуглеродистая пластмассовая сталь St.3 диаграмма

давления сжатия, а также диаграмма растяжения, простирающаяся прямая линия, и ди. — Рис 45А Аграм округляется и передается в участок с небольшим горизонтальным наклоном — область текучести. При сжатии предел текучести не так выражен, как при растяжении. Пределы пропорциональности, упругости и текучести стали при сжатии практически такие же, как при растяжении. угол Ирис 46А

Поскольку наклон линейной части диаграммы одинаков при растяжении и сжатии, модули упругости равны. Стальные образцы (рис. 45, а) укорачиваются при сжатии, а их боковые размеры увеличиваются, особенно в середине. В конце образца боковая деформация сдерживается наличием трения в контакте с поверхностью испытательной машины, поэтому при сжатии цилиндр принимает форму бочки (рис. 45,6). Постепенно сглаживается (на рис. 45,), но он разрушает неконтролируемый, неспособный установить его конечную долговечность. Обычно

прочность на сжатие такая же, как прочность на растяжение. Образцы из других пластмассовых металлов (медь, алюминий) деформируются при сжатии подобно образцам стали и имеют аналогичную диаграмму напряжений b при сжатии. Диаграмма сжатия чугуна по форме аналогична диаграмме растяжения чугуна. Эти графики искажены с самого начала. Внезапно обрывается в начале и достигает максимальной нагрузки (см. Рисунок 44),

однако вертикальная ось диаграммы напряжений в несколько раз больше при сжатии, чем при растяжении. Прочность на сжатие чугуна AB = Людмила Фирмаль

(50004-15 000) кПсм2 (5004-1500Мн / м2), то есть в 4-5 раз больше, чем натяжение. Таким образом, чугун работает намного лучше при сжатии, чем при растяжении. При сжатии образцов чугуна (рис. 46, а) продольная деформация не имеет значения. Образец принимает слегка бочкообразную форму и слегка выпирает в центральной части, после чего появляются трещины под углом около 45 ° на оси участка с наибольшим касательным напряжением. 46, б). В это время нагрузка быстро падает, и график прерывается. В момент разрушения стороны

Читайте также: Как поступает бензин в цилиндры у иж юпитер 5

образца разделяются, что принимает форму двух срезанных конусов (рис. 46, б). Большинство хрупких материалов (бетон, камень), таких как чугун, разрушаются при сжатии и имеют сходную форму сжатия. Предел прочности при сжатии этих материалов намного больше, чем предел прочности при растяжении (для бетона примерно в 20 раз). Все хрупкие материалы плохо работают при растяжении. история * Поэтому, например, в удлиненной бетонной конструкции усиливающая сила, сила растяжения, которая выстроила восприятие. Эта структура называется железобетоном. На рис. 47, а и б показаны

бетонные кубы до и после разрушения в виде двух усеченных пирамид, которые находятся в форме дробящих бетонных или цементных кубиков в 50 часов. Например, чтобы устранить эффект трения между сжимаемыми бетонными кубиками и плоскостями машин, смажьте эти плоскости парафином и бетоном. Куб разрушается вдоль плоскости, параллельной приложенной силе (рис. 47, б). Поскольку в горизонтальном направлении нет напряжения, характер этого разрушения может быть объяснен только в результате специального исследования этого вопроса, проведенного в главе Xii. При испытании древесины на сжатие необходимо учитывать, что

древесина является анизотропным материалом и работает по-разному вдоль и между волокнами. Наряду с рисунком 1, диаграмма напряжения сжатия древесины по двум волокнам показана на рисунке. 48 Многие породы древесины, сжатые вдоль волокна, выдерживают значительные нагрузки, например, прочность на разрыв сосны достигает 4004-800K Г1см? (404-80L4n / LG2). В этом случае, когда происходит разрушение древесины, некоторые кубики на другом сдвигаются (рис. 49, а). Когда древесина сжимается по волокну, древесина не разрушается, а сильно прижимается (рис. 49, б)

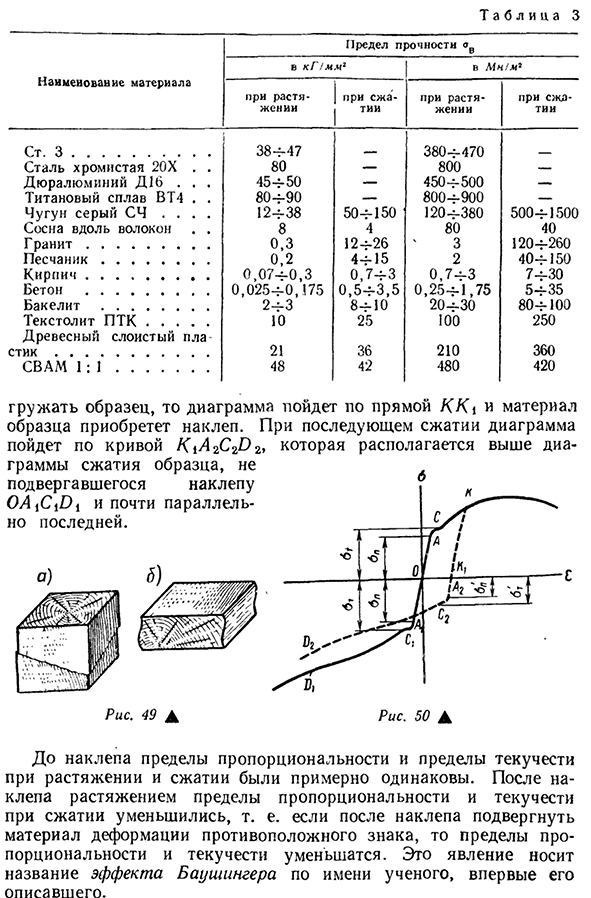
. За столом. 3 Для сравнения приведены пределы прочности на растяжение и сжатие некоторых материалов. Большой интерес представляет поведение образца после разгрузки, достигающего напряжения ниже сжатия (или наоборот) и ниже пластической деформации. Рассмотрим диаграмму напряжений при растяжении и сжатии стали. 50). Если вы начнете несколько точек на диаграмме

растяжения, время 51T a b l I C a3 Название материала Mn / м2 кг / мм2 предел прочности AV Когда растягивается Ся | TII Когда растягивается Во время сжатия Статья 3 … один 384-47 3804-470 Хромированная сталь 20Х. 80-800-дюраль D16. 454-50-4504-500-титановый сплав ВТ4 … 804-90-800-4-900 чугун серый SCH. 124-38 504-150 1204-380 500-4-1500 сосны вдоль зерна. 8 4 80 40G R a I t ………………. до 0,3,124-26 3 120-4-260 Песчаник ………… 0,2 44-15 2 404-150 Кирпич. ……………………………… 0, 0 7 4 -0, 3 0,74-3 0,7 4 -3 74-30 Бетон ……………… 0,0254-0,175 0, 5 4- 3, 5 0,254-1,75 54-35 бакелит ………… 24-3 84th204-30 804-100 Текст Легкий ПТК. ……. 10 25 100 250 Деревянный ламинированный пластик.

………………………………………….. 21 36 210 360 Плавание 1: 1 ………………………. 48 42 480 420 Материал, который находится над образцом с алмазной загрузкой и последующей диаграммой сжатия, является прямым КК \, диаграмма и образец получает наклеп. PR переходит на кривую K iA2C2D2, грамм сжатия образца, который не получил наклепу OAtCfDi и, наконец, почти параллелен. шесть Рис 49 и рисунок. 50D До отверждения предел пропорциональности и предел текучести при сжатии были практически одинаковыми. После отверждения растяжением пределы пропорциональности и

Читайте также: Гидравлический цилиндр 10 т jtc 1035r

текучести при сжатии уменьшаются, то есть если материал подвергается деформации противоположного знака после отверждения, это явление пропорционально ученому, который его первоначально описал. После баушингер эффект называется.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:Гидроцилиндр не держеит навеску. Доработка поршня.Скачать

Тема 2.2. Растяжение и сжатие

Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы N, а прочие силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю.

Это самый простой и часто встречающийся вид деформации. Обычно он наблюдается когда внешняя нагрузка действует вдоль продольной оси стержня. Продольной осью стержня называется линия, проходящая через центры тяжести поперечных сечений.

Обычным является растяжение стержня силами, приложенными к его концам. Передача усилий к стержню может быть осуществлена различными способами, как это показано на рис. 1.

Рис. 1. Растяжение стержня

Во всех случаях, однако, система внешних сил образует равнодействующую F, направленную вдоль оси стержня. Поэтому независимо от условий крепления растянутого стержня, расчетная схема в рассматриваемых случаях (рис. 1, а, б) оказывается единой (рис. 1, в) согласно принципу Сен – Венана.

Если воспользоваться методом сечений (рис. 2), то становится очевидным, что во всех поперечных сечениях стержня возникают нормальные силы N_z, равные силе F (рис. 2, б).

Сжатие отличается от растяжения, формально говоря, только знаком силы N_z. При растяжении нормальная сила N_z направлена от сечения (рис. 2, б), а при сжатии – к сечению.

Рис. 2. Нормальная сила N

Растягивающие продольные силы принято считать положительными (рис. 3, а), а сжимающие – отрицательными (рис. 3, б).

Рис. 3. Знак продольной силы N

При расчете стержней, испытывающий деформацию растяжения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от N_z), возникающих в стержне, и нахождение линейных перемещений в зависимости от внешней нагрузки.

Продольные силы (N_z), возникающие в поперечных сечениях стержня, определяются по внешней нагрузке с помощью метода сечений.

График, показывающий изменение продольных сил по длине оси стержня, называется эпюрой продольных сил (эп. N_z). Он дает наглядное представление о законе изменения продольной силы.

Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.

Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти N_max при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.

Читайте также: Ремонт главного тормозного цилиндра ниссан альмера н16

Перед построением эпюр необходимо освободить брус, в котором будем строить эпюры от опорных связей (выделить объект равновесия) и приложить к нему все действующие внешние силы (активные и реактивные). Затем необходимо установить границы участков, в пределах которых закон изменения внутренних сил постоянный. Границами таких участков являются сечения, где приложены сосредоточенные силы или начинается и кончается распределенная нагрузка, а также сечения, где имеется перелом стержня.

Применяя метод сечений и учитывая правила знаков изложенные выше, получаем уравнения изменения внутренних сил в пределах длины каждого участка бруса. Затем, используя, полученные зависимости строим графики (эпюры) этих усилий. Ординаты эпюр в определенном масштабе откладываем от базисной линии, которую проводим параллельно оси бруса.

На основании метода сечений продольная сила в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций внешних сил, приложенных к стержню по одну сторону от рассматриваемого сечения, на его продольную ось.

Причем проекция внешней силы берется со знаком плюс, если сила растягивает часть стержня от точки ее приложения до рассматриваемого сечения и, наоборот, со знаком минус – если сжимает.

§2. Напряжение в поперечных сечениях стержня

При растяжении или сжатии осевыми силами стержней из однородного материала поперечные сечения, достаточно удаленные от точек приложения внешних сил ,остаются плоскими и перемещаются поступательно в направлении деформации. Это положение называют — гипотезой плоских сечений. На основании указанного можно заключить, что все точки какого-либо поперечного сечения стержня находятся в одинаковых условиях и, следовательно, напряжения распределяются по сечению равномерно. Эти напряжения перпендикулярны поперечному сечению, а значит, являются нормальными напряжениями. Их значения найдем, разделив продольную силу N на площадь А: σ=N/A

Продольная сила N с помощью метода сечений всегда может быть выражена через внешние силы. В формулe следует подставлять алгебраическое значение N т.е со знаком плюс в случае растяжения и со знаком минус в случае сжатия

§3. Расчеты на прочность и жесткость при растяжении-сжатии

Прочность стержня при осевом растяжении и сжатии обеспечена, если для каждого его поперечного сечения наибольшее расчетное (рабочее) напряжение σ не превосходит допускаемого [σ] : σ=N/A≤ [σ],

где N — абсолютное продольной силы в сечении;

А — площадь поперечного сечения;

[σ] — допускаемое напряжение пр растяжении или сжатии для материала стержня.

Данное выражение определяет условие прочности при растяжении или сжатии.

С помощью этой формулы решается три вида зада (выполняется три вида расчета):

1. Проверка прочности (проверочный расчет). При заданных продольной силы N и площади поперечного сечения А определяют рабочее (расчетное) напряжение и сравнивают его с допускаемым [σ].

Превышение рабочего (расчетного) напряжения не должно быть больше 5% , иначе прочность рассчитываемой детали считается недостаточной.

В случаях, когда рабочее напряжения значительно ниже допускаемых σ