Диметрия цилиндра в цилиндре (2 видео)

Прямоугольная диметрия характеризуется тем, что коэффициенты искажения, определенные из выражения (1), u = w = 0,94, a v = 0,47. Определяют их следующим образом:

u 2 + (u/2) 2 + u 2 = 2;
u 2 = 8/9; u = w = √8/9 ≈ 0,94; v = 0,47.

В соответствии с ГОСТ 2.317-69 практические построения в прямоугольной диметрии следует выполнять пользуясь приведенными коэффициентами искажения: u = w = 1 и v = 0,5.

Расположение осей стандартной прямоугольной диметрии показано на рис. 8.

Аксонометрический масштаб для прямоугольной диметрии будет М А 1,06:1.

В прямоугольной диметрии равные окружности диаметра d, лежащие в координатных плоскостях х0у и у0, проецируются в равные эллипсы, большая ось которых 2а = 1,06d, а малая — 2b = 0,35d, если пользуемся приведенными коэффициентами искажения. Окружность, расположенная в плоскости xOz, проецируется эллипс с осями: большая ось 2а’ = 1,066d, малая ось 2b’ = 0,95d (рис. 9).

Диаметры окружности, параллельные координатным осям, спроецируются в отрезки, параллельные осям диметрии l 1 = l 2 = d; l = 0,5d, при этом l 1 ׀׀ Ox; l 2 ׀׀ Oу; l 3 ׀׀ Oz.

Кроме указанных,можно построить еще четыре точки, симметричные точкам, ограничивающим проекции диаметров, параллельных координатным осям. Тогда эллипсы, как диметрию окружности, можно построить по его двенадцати точкам.

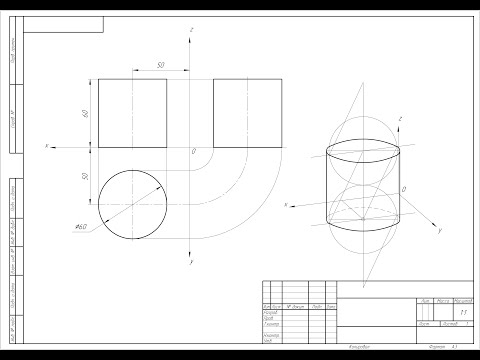
Изображение геометрических поверхностей в прямоугольной диметрии рассмотрим на примере построения стандартной прямоугольной диметрии прямого кругового цилиндра. На рис. 10 приведен пример комплексного чертежа полого цилиндра высотой Н с наружным d и внутренним d₁ диаметрами. Цилиндр расположим в натуральную величину в натуральной системе координат Oxyz, относительно которой построим диметрическую его проекцию.

Как и в случае построения окружностей в изометрии, в диметрии также начнем построение фигуры с эллипсов верхнего и нижнего оснований цилиндра, которые являются изометрическими проекциями окружностей этих оснований. Окружности оснований расположены в плоскостях, параллельных горизонтальной плоскости проекций, поэтому, пользуясь приведенными ранее правилами, определим, что большие оси эллипсов будут перпендикулярны оси Oz. Малые оси эллипсов совпадут с направлением оси Oz, Центры осей эллипсов нижнего и верхнего оснований расположены на расстоянии Н. Величины осей определяем в зависимости от величины наружного и внутреннего диаметров цилиндров. Построив эллипсы, приведем очерковые линии, касательные к внешним эллипсам. Для наглядности построим вырез четверти цилиндра, построение которого видно из (рис. 10). Невидимые линии покажем штриховыми линиями. Для наглядности такими же линиями покажем линии вырезанной части цилиндра. Видимые контурные линии наводят нужной толщиной.

Видео:Как начертить цилиндр в объемеСкачать

Диметрия цилиндра в цилиндре

u 2 + (u/2) 2 + u 2 = 2;
u 2 = 8/9; u = w = √8/9 ≈ 0,94; v = 0,47.

Расположение осей стандартной прямоугольной диметрии показано на рис. 8.

Аксонометрический масштаб для прямоугольной диметрии будет М А 1,06:1.

Читайте также: Расчет кубатуры цилиндра калькулятор

Видео:Построение цилиндра в трех проекциях и его прямоугольной диметрии.Скачать

Диметрия цилиндра в цилиндре

Как построить диметрию детали?

Пять лет назад я написал урок на тему «Как построить изометрию?». Я знал, что пишу очень нужную статью, что такого подробного описания в сети просто нет. Но я и подумать не мог, что этот урок станет бестселлером. Каждый год к нему обращаются более 40 тысяч студентов, и я точно знаю, что не меньше трети из них обретают умение или, как минимум, перестают шарахаться от изометрии как от огня и начинают понимать, с какого бока к ней вообще надо подходить. И в том числе поэтому я крайне не рекомендую браться за урок построение диметрии если построение изометрии является для вас чем-то немыслимым. Дело в том, что в статье «построение изометрии детали» я очень подробно разобрал некоторые моменты, связанные с осями, их приложением к детали, и прочие нюансы, которые уже не будут так тщательно разобраны здесь.

Анализируя запросы, благодаря которым вы попадаете на мой сайт, я понял, что я конечно молодец, но буду в два раза более молодец, если помогу вам разобраться с вопросом Как начертить диметрию детали?. Диметрическая проекция, диметрия, построение диметрии по шагам — это все то, что вы найдете абзацами ниже. Ну что же, прошу к внимательному чтению!

В первую очередь нам нужно разобраться, что такое диметрия, в чем ее особенности и для чего ее удобно использовать. Диметрическая проекция — вид аксонометрических проекций, в котором оси X,Y и Z имеют направления 7°10′ и 41°25′.

При этом, как указано на рисунке, расстояния откладываемые вдоль осей X и Z откладываются без искажений (с приведенным коэффициентом 1), а расстояния вдоль оси Y откладываются с коэффициентом 0.5, т.е. уменьшаются в два раза. Благодаря такому расположению осей и линейным коэффициентам диметрия значительно эффективнее раскрывает наглядный вид деталей, в конструкции которых имеются четырех- и шестиугольные призмы. Кроме того, диметрия несколько экономичнее изометрии в плане занимаемого на листе пространства, но наверное актуальность этого уже в прошлом.

Итак, мы получили задание начертить диметрию вот такой детали. Ее можно описать как нечто похожее на бинокль, но вместо колесика для наведения резкости тут мы имеем сквозное отверстие диаметром 32мм. Сложно? В меру. Не совсем просто, но и не слишком накручено. То, что надо.

Во-первых, мы не сможем обойтись без осей. Казалось бы, вот вам значения углов на первом рисунке, но есть известный способ построения диметрических осей, позволяющий делать это быстро и без использования циркуля. Особенно удобен метод на листке в клетку, но и нам подойдет. Необходимо из точки 0 отложить вправо и влево по 8 частей (например сантиметров или клеток), а вниз — одна часть в левой части и семь частей в правой части рисунка соответственно.

Воспользовавшись указанным способом построим два центра для наших будущих «окуляров». Они должны быть на расстоянии 75 мм отложенных вдоль оси X. (По сути нужно построить один центр по указанной технологии, затем отложить 75мм и через полученную точку провести оси, параллельные исходным)

Читайте также: В одном цилиндре масло дизель

Следующим шагом мы построим изображения окружностей радиусом 20 мм (внешняя окружность по окуляру нашего «бинокля»). В диметрии, как и в изометрии, окружность проецируется в эллипс. Для построения эллипса мы воспользуемся данными из справочника, в котором говорится, что при таком расположении эллипса, его малая ось будет равна 0.35*диаметр_окружности = 0.35*d, а большая ось будет равна 1.06*d. Для наших окружностей диаметром 40 мм это будут оси длиной 14мм и 42.4мм соответственно. При этом по оси X следует отложить расстояние 40мм без искажения, а по оси Y — 20мм (поскольку, как было сказано выше, в диметрии по оси Y расстояния откладываются с коэффициентом 0.5). На картинке я подробно обозначил и текущие размеры для нашей детали, и формулы для них.

Внимание: я не расписываю подробно, как построить красивый эллипс, зная две его оси. Этому у меня посвящен отдельный урок: как построить эллипс. Не совсем наш случай, но очень в тему еще один урок: «как начертить окружность в изометрии». Впрочем, если вы добрались до изучения диметрии, вы уже должны иметь представление о построении эллипсов.

Следующим шагом построим маленькие эллипсы — изображения внутренних окружностей «окуляров». Строим по той же технологии, основываясь на значении диаметра 14мм, а длины большой и малой оси будут 7,42мм и 2,45мм (на картинке размеры не показаны, что касается точности — мы же с вами разумные люди, поэтому всего должно быть в меру).

Согласно исходному чертежу наши «окуляры» на 10мм возвышаются над горизонтальной площадкой. Центр этой площадки расположен на 10 мм ниже середины отрезка, соединяющего центры наших эллипсов. А отложив по 10мм (почему не по 20? Потому что коэффициент 0.5, не забываем! )в каждую сторону вдоль оси Y, мы получим засечки, которые помогут нам прочертить границы этой горизонтальной площадки:

И, собственно, сами границы:

Теперь опустим вертикальные отрезки по 10мм от крайних точек больших эллипсов:

И проведем копию эллипсной дуги на 10 мм ниже уже имеющихся эллипсов. Можно строить, а можно просто из каждой точки отложить вниз точку на удалении 10мм — и соединить их. Основываясь на полученном, обводим наши границы горизонтальной площадки, а так же линии, где из площадки вырастают цилиндры «окуляров»:

Строим центры нижних окружностей «окуляров». Они будут на 54мм ниже верхних центров. Кроме того, мы можем сразу провести крайние вертикальные боковые границы. Сами эллипсы строим или переносим, но пока в тонких линиях:

Пришло время заняться центральным отверстием. В отличии от уже построенных, центральная окружность лежит в другой плоскости, осью вращения в которой является ось Y. Ничего страшного нет, но нужно учесть два момента:
1. Большая ось эллипса будет перпендикулярна оси Y (такой оси мы сегодня еще не обозначали, это новое направление. Чтобы ни с чем не перепутать, оси данного эллипса я обозначил на рисунке красным цветом). Центр будет располагаться на 30 мм ниже горизонтальной площадки:

2. Искажение по малой оси будет 0.95 (0.95*d), что практически дает в результате окружность (большая ось по прежнему равна 1.06*d), но я ни разу в своей практике не заменял этот почти круглый эллипс окружностью, и вам не советую. Преподаватель должен видеть, что вы знаете о том, что это эллипс. Уж если скажет, что можно окружность провести — тогда само собой. Но первично — чертите эллипс, и да похвалит вас преподаватель за ваши знания (и хмыкнет по части вашей скрупулезности). В результате вычислений и мучительных построений должен получиться такой вот эллипс (оси 33,92мм и 30,4мм):

Читайте также: Рулевой цилиндр двухстороннего действия

Остается построить еще один аналогичный эллипс с тем же центром. Исходные данные: диаметр 60мм, большая ось 63,6мм малая ось 57мм

Обозначив набросками наш последний эллипс, обводим его видимую часть, а так же ранее обозначенные нижние границы «окуляров» и стираем лишнее. Так же для приличия проведем отрезок, обозначающий границу цилиндрической поверхности (указан стрелкой). Возможно, про него никто бы и не вспомнил, но он есть, нужно прочертить:

Обратите внимание, у центрального отверстия появилась дальняя граница. Это копия эллипса, смещенная на 20мм вдоль оси Y. (Ширина детали 40мм, коэффициент по оси Y равен 0.5)

По сути, на этом наш урок «пошаговое построение диметрии» закончен. Однако, было бы неправильным, лишить вас самого интересного, и не отрезать четвертушку ? Да, это потребуется не каждому, но зато для тех, кому придется данную процедуру выполнять, следующая картинка даст хороший наглядный материал, и наверняка поможет в неравной борьбе с домашним заданием:

Вот, теперь все. Ничего нового сюда уже не добавить. Если на вашей кафедре требуют, то в свободной зоне нужно вычертить и обозначить оси (направления, углы, названия), а в случае с вырезом четверти, не помешает и обозначение направления штриховки (в данном уроке не разбирается, но там ничего сложного, практически копия самой первой картинки в уроке).

До встречи на новых уроках!

Вы можете сказать «спасибо!» автору статьи:

пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект «White Bird. Чертежи Студентам»

или запишите наш телефон и расскажите о нас своим друзьям — кто-то наверняка ищет способ выполнить чертежи

или создайте у себя на страничке или в блоге заметку про наши уроки — и кто-то еще сможет освоить черчение.

А вот это — не реклама. Это напоминание, что каждый из нас может сделать. Если хотите — это просьба. Мы действительно им нужны:

Автор комментария: Vv
Дата: 2015-11-20

Большое спасибо, добрый человек!

Все-таки приятно, когда тебя называют добрым без сарказма!

Автор комментария: Роман
Дата: 2015-12-24

Очень полезно. Спасибо автору.

Автор комментария: Кир
Дата: 2016-04-01

Автор комментария: ивангай
Дата: 2016-11-21

Приветствую! Начните с урока про изометрию. Без этого у вас нет шансов. К сожалению это очень сложный материал, на него нельзя запрыгнуть на ходу.

Автор комментария: Юлия
Дата: 2017-05-02

Добрый день. Спасибо за урок (тут даже разрез сделан). Он очень полезен. Не нашла правда тут материала по построению триметрии. Будет ли?

Автор комментария: Юлия
Дата: 2017-05-02

Автор комментария: Александр
Дата: 2018-11-22

Статья полезная,но верхний чертёж начерчен неточно: не указана линия пересечения нижней центральной цилиндрической поверхности с нижней плоскостью.

Добавьте свой комментарий:

Антон, спасибо за отлично выполненные чертежи. У меня единственная пятерка на курсе :))). Всем рекомендую обращаться только сюда! Работы выполнены безупречно! Сама рабатаю в комании, где есть конструкторский отдел и решила показать им чертежи Антона. Собрался целый консилиум, говорили где надо подправить, что-то вообще не так, но я решила сдать ничего не исправляя. И это было правильное решение :))). Еще раз спасибо, Антон.

Ирина, я преклоняюсь перед вашим желанием оставить комментарий спустя 3 месяца после нашего сотрудничества. От этого он еще более ценен! И главное — в нем яркий пример того, насколько сильное значение имеет субъективность восприятия чертежа разными людьми. Мы делаем чертежи в соответствии с ГОСТами, но у каждого преподавателя может быть свое видение «более удачного варианта исполнения», и поэтому иногда студентам приходится что-то менять в наших работах.