10. Про прямые круговые цилиндры C1 и C2 известно, что у C1 радиус основания в два раза больше, чем у C2, но у C2 высота в три раза больше, чем у C1. Найдите отношение объёма цилиндра C2 к объёму C1:
а) 1
б) 0,75 +
в) 1,2
11. Если диаметр основания и образующая цилиндра равны друг другу, то осевым сечением является:
а) квадрат +
б) круг
в) прямоугольник
12. В цилиндрический сосуд, в котором находится 10 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 2,4 раза. Чему равен объем детали:
а) 24 л
б) 14 л +
в) 12 л
13. Геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её:
а) цилиндр +
б) конус
в) квадрат
14. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 1. Объем параллелепипеда равен 5. Найдите высоту цилиндра:
а) 1,20
б) 1,5
в) 1,25 +
15. Сечение, проходящее параллельно оси цилиндра, может быть:
а) либо прямоугольником, либо квадратом +
б) только квадратом
в) только прямоугольником
16. В цилиндрическом сосуде уровень жидкости достигает 27 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 3 раза больше первого:
а) 18 см
б) 3 см +
в) 9 см
17. Если диаметр основания и образующая цилиндра не равны друг другу, то осевым сечением является:
а) квадрат
б) круг
в) прямоугольник +
18. В цилиндрический сосуд налили 1200 см3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 10 см. Чему равен объем детали:
а) 1100 см3
б) 1000 см3 +
в) 100 см3
19. Вычислите длину высоты равностороннего цилиндра, площадь осевого сечения которого равна 25:
а) 50
б) 12,5
в) 5 +
20. Пусть V, r, h соответственно объем, радиус и высота цилиндра. Найдите объем, если r=2√2 cм, h=3 см:
а) 43π см3
б) 24π см3 +
в) 31π см3
21. Сколько образующих можно провести в цилиндре:
а) много +
б) одну
в) две
22. Радиус основания цилиндра равен 7, а высота – 10. Найдите площадь боковой поверхности цилиндра, деленную на π:
а) 124
б) 140 +
в) 104
23. Какой вид не может иметь сечение цилиндра:
а) овал
б) квадрат
в) треугольник +
24. Шар вписан в цилиндр. Площадь поверхности шара равна 41. Найдите площадь полной поверхности цилиндра:
а) 60
б) 61,5 +
в) 55
25. Вращением какой геометрической фигуры можно получить цилиндр:
а) прямоугольного треугольника вокруг гипотенузы
б) прямоугольного треугольника вокруг катета
в) прямоугольника вокруг одной из сторон +
26. Площадь боковой поверхности цилиндра равна 18π, а диаметр основания равен 9. Найдите высоту цилиндра:
а) 4
б) 2 +
в) 36
27. Площадь полной поверхности цилиндра:
а) S=2п(r+h) +
б) S= r(r+h)
в) S=пr(r+h)
28. Поверхность, образуемая однопараметрическим семейством параллельных прямых (называемых образующими) и проходящими через точки некоторой кривой (называемой направляющей):
а) поверхность основания цилиндра
б) коническая поверхность
в) цилиндрическая поверхность +
29. Площадь боковой поверхности цилиндра:
а) S=пrh +
б) S=2r
в) S=r2
30. Отрезок, высекаемый плоскостями его оснований на прямой, перпендикулярной им, или длина этого отрезка:
а) сторона цилиндра
б) высота цилиндра +
в) вершина цилиндра
- Тестирование по геометрии 11 класс
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Оставьте свой комментарий
- Подарочные сертификаты
- Методические указания к выполнению практических заданий по теме «Тела вращения»
- Тестовые вопросы к теме «Цилиндр»
- 📹 Видео
Видео:Видеоурок по математике "Цилиндр"Скачать

Тестирование по геометрии 11 класс
Ищем педагогов в команду «Инфоурок»
Г-11 Тест №3. Цилиндр Вариант1.
1. Выберите верное утверждение :
а) Длина образующей цилиндра называется радиусом цилиндра ; б) цилиндрическая поверхность называется боковой поверхностью цилиндра ;
в) сечение цилиндра , перпендикулярное оси цилиндра , называется осевым ;
г) площадь боковой поверхности цилиндра вычисляется по формуле S бок. = π r 2 h ;
д) цилиндр может быть получен в результате вращения треугольника вокруг одной из сторон .
2. Сечение проведено параллельно оси цилиндра , отстоит от него на расстоянии , равным 3 . Найдите площадь сечения , если радиус цилиндра равен 5 , а его высота – 10 .
а) 40 ; б) 80 ; в) 60 ; г) 30 ; д) 10√91 .
3. Площадь осевого сечения равностороннего цилиндра равна 4 см 2 . Найдите площадь основания цилиндра .
Читайте также: Почему не держит гидрозамок цилиндра
а) 2π см 2 ; б) π см 2 ; в) 4π см 2 ; г) 0,5π см 2 ; д) определить нельзя.
4. Диагональ сечения цилиндра , параллельного оси , равна 8√3 , она наклонена к плоскости основания под углом 60˚. Это сечение в основании отсекает дугу в 120˚. Найдите площадь осевого сечения цилиндра .
а) Определить нельзя ; б) 48 ; в) 16√3 ; г) 96√3 ; д) 96 .
5. Радиус r основания цилиндра в три раза меньше его высоты h . Площадь полной поверхности цилиндра равна 288π см 2 . Найдите r и h .
а) r = 18см , h = 6см ; б) r = 6 см , h = 18см ; в) r = 2см , h =6см ; г) определить нельзя ;
Г-11 Тест №3. Цилиндр Вариант 2.
1. Выберите верное утверждение .
а) Радиус цилиндра не может равняться высоте цилиндра ;
б) площадь юоковой поверхности цилиндра равна произведению площади основания цилиндра на его высоту;
в) сечение цилиндра , параллельное оси цилиндра, называется осевым ;
г) площадь полной поверхности цилиндра вычисляется по формуле S цил. = π r ( h + r ) ;
д) цилиндр может быть получен в результате вращения прямоугольника вокруг одной из сторон .
2. В цилиндре параллельно его оси проведено сечение. Диагональ сечения, равная 16, составляет угол 60 0 с плоскостью основания. Радиус основания цилиндра равен 5. Найдите расстояние от оси цилиндра до плоскости сечения.
. 3. Площадь основания равностороннего цилиндра равна 2 π см 2 . Найдите площадь осевого сечения цилиндра .
а) 8π см 2 ; б) 8 см 2 ; в) 2 см 2 ; г) 4 см 2 ; д) определить нельзя .
4. C ечение цилиндра плоскостью , параллельного оси , удалено от нее на √3. Это сечение отсекает в основании дугу в 60 0 . Найдите площадь осевого сечения цилиндра, если площадь данного сечения равна 8.
а) Определить нельзя ; б) 8 ; в) 16√3 ; г) 8√3 ; д) 16 .
5. Площадь боковой поверхности цилиндра вдвое больше площади основания. А площадь полной поверхности равна 256 π см 2 . Найдите радиус r и высоту цилиндра h .
а) r = 8см , h = 6см ; б) r = 6 см , h = 6см ; в) r = 6см , h =8см ; г) r = 8см , h = 8 см ;
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Международная дистанционная олимпиада Осень 2021
Вам будут интересны эти курсы:
Оставьте свой комментарий
В России запустили «Школу общественной дипломатии» для малочисленных народов
Власти Амурской области предложили продлить каникулы в школах в связи с эпидобстановкой
Минобрнауки разрешило вузам перейти на дистанционное обучение
В школе в Пермском крае произошла стрельба
Школьников не планируют переводить на удаленку после каникул
Минобрнауки утвердило перечень олимпиад для школьников на 2021-2022 учебный год
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:№531. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельнойСкачать

Методические указания к выполнению практических заданий по теме «Тела вращения»
Ищем педагогов в команду «Инфоурок»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ НИЖЕГОРОДСКОЙ ОБЛАСТИ
Государственное бюджетное образовательное учреждение
среднего профессионального образования
«ПЕРЕВОЗСКИЙ СТРОИТЕЛЬНЫЙ КОЛЛЕДЖ»
к выполнению практических заданий
Тела вращения: Методические указания к выполнению практических заданий по дисциплине «Математика»/ Перевозский строит. колледж; Сост.: Е.В. Исайчева. — Перевоз, 2013. — 42 с
Методические указания по теме «Тела вращения» предназначены для организации самостоятельной работы обучающихся 1 курса всех специальностей. Их цель — помочь обучающимся освоить тему, систематизировать свои знания, ознакомиться с некоторыми методами решения простейших задач, а также помочь при подготовке к ЕГЭ.
ДИСКРЕТНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА 32
ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ 42
Данные методические указания включают в себя краткий теоретический материал по теме «Тела вращения», практический блок, состоящий из решенных задач и заданий для самостоятельного решения. Методические указания предназначены для обучающихся 1 курса всех специальностей, изучающих дисциплину «Математика», но ими могут воспользоваться и обучающиеся старших курсов при подготовке к ЕГЭ.
Цель методических указаний — помочь обучающимся освоить тему, систематизировать свои знания, ознакомиться с некоторыми методами решения простейших задач.
Попыткой достигнуть этой цели и определяется структура данного пособия: в начале каждого параграфа кратко изложен теоретический материал (определения, основные теоремы и формулы), знание которого необходимо для решения задач данного раздела. Это позволяет использовать пособие, не прибегая к учебникам. Далее указываются методы решения задач какого-либо вида и разбираются конкретные примеры на использование этих методов. Приведенные решения также могут служить иллюстрацией правильного оформления решения в письменных работах. После этого даны задания для самостоятельного решения, причем расположены они по возрастанию их сложности. В конце пособия приведены тестовые вопросы и варианты контрольной работы по данной теме.
Если после изучения темы с использованием данных методических указаний останутся невыясненные моменты, следует обратиться за консультацией (устной или письменной) к преподавателю.
Цели: в ходе изучения данной темы обучающиеся должны освоить основные понятия и определения темы, элементы цилиндра, сечение цилиндра, формулы площади боковой и полной поверхности цилиндра научиться решать задачи; использовать приобретенные знания и умения в практической деятельности
Читайте также: Упала компрессия во всех цилиндрах калина
Изучите теоретический материал:
Определение : Цилиндр – тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
Цилиндр получается при вращении прямоугольника OBB O вокруг стороны OO.
прямая OO — ось цилиндра
отрезок OO— высота,
отрезок АА= ВВ — образующая
круг (О,ОВ) =кругу (O, OВ) – основание цилиндра
Рассмотрим сечение цилиндра различными плоскостями. Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник (рис. 2,а), две стороны которого – образующие, а две другие – диаметры оснований цилиндра. Такое сечение называется осевым.
Если секущая плоскость перпендикулярна к оси, то сечение является
в) сечение цилиндра плоскостью, перпендикулярной к оси цилиндра, то сечение является кругом (рис. 2,б)
Развёртка цилиндра состоит из двух кругов (основания цилиндра) и прямоугольника (боковая поверхность) (рис 3). Длины окружностей равны длине прямоугольника.
Площадь поверхности цилиндра
Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра.
Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований.
2 Рассмотрите задачи с решениями:
Площадь боковой поверхности цилиндра равна 72π, а диаметр основания — 9. Найдите высоту цилиндра.
Площадь боковой поверхности цилиндра находится по формуле:
Площадь боковой поверхности цилиндра равна 64π, а высота — 8 . Найдите диаметр основания.
Площадь боковой поверхности цилиндра находится по формуле:
Диаметр равен двум радиусам. Значит,
Р

Площадь боковой поверхности цилиндра 
Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
Площадь боковой поверхности цилиндра равна 
Найдите площадь полной поверхности цилиндра, если диагональ его осевого сечения, равная 8см, составляет с образующей цилиндра угол величиной 30 градусов.
Поскольку AC = 8 см, а угол ACD = 30°, то
Пояснение . Треугольник ACD — прямоугольный. Соответственно, CD / AC = cos ∠ ACD по свойству тригонометрических функций в прямоугольном треугольнике. Значение cos 30 найдем из таблицы значений тригонометрических функций.
Откуда радиус основания цилиндра равен 4/2 = 2 см
Площадь основания цилиндра, соответственно, равна
S1 = πR 2 = 4π
Площадь боковой поверхности цилиндра равна площади его развертки — произведению длины окружности основания и высоты цилиндра. То есть:
S2 = 2πRh = 2π * 2 * 4√3 = 16π√3
Общая площадь поверхности цилиндра равна:
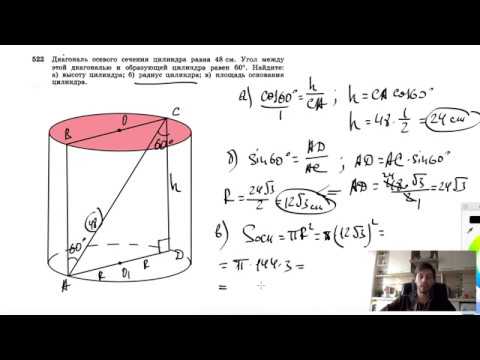
Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующей цилиндра равен . Найдите: а) высоту цилиндра; б) радиус цилиндра; в) площадь основания цилиндра.
Высота цилиндра равна 8 см, радиус равен 5 см. Найдите площадь сечения цилиндра плоскостью, параллельной его оси, если расстояние между этой плоскостью и осью цилиндра равно 3 см.
Осевое сечение цилиндра – квадрат, диагональ которого равна 20 см. Найдите: а) высоту цилиндра; б) So цилиндра
1. Проведем диагональ АС сечения АВС D .
2. D ADC – равнобедренный, прямоугольный, А D = DC , h = 2 r ,
Þ Ð CAD = Ð ACD =45 ° , тогда
3. Найдем радиус основания
4. Найдем площадь основания
Осевое сечение цилиндра − квадрат, площадь которого Q.
Найдите площадь основания цилиндра.
Дано: цилиндр, квадрат − осевое сечение цилиндра, S квадрата = Q.
Сторона квадрата равна . Она равна диаметру основания. Поэтому площадь основания равна .
Высота цилиндра 6см, радиус основания 5см.
Найдите площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4см от нее.
Дано: Н = 6см, R = 5см, ОЕ = 4см.
Треугольник ОКМ − равнобедренный (ОК = ОМ = R = 5 см),
треугольник ОЕК − прямоугольный.
Из треугольника ОЕК, по теореме Пифагора:
Диаметр основания цилиндра 1м.
Найдите площадь боковой поверхности цилиндра.
S бок. = 2π R × 2π R = (2π R ) 2 = 4π 2 ×0,25 = π 2
3 Задания для самостоятельной работы обучающихся
Решите следующие задачи, используя теоретический материал и примеры, приведенные выше:
1. Площадь боковой поверхности цилиндра равна 2п, а высота — 1. Найдите диаметр основания.
2. Площадь боковой поверхности цилиндра равна 2π, а диаметр основания — 1. Найдите высоту цилиндра.
3. Найдите площадь осевого сечения цилиндра, где радиус основания равен 5см, а высота 15 см.
4. Найдите радиус основания цилиндра, если площадь боковой поверхности этого цилиндра равна 80π, а высота цилиндра 10.
5. Найдите высоту цилиндра, если радиус основания цилиндра равен 5 см, а площадь полной поверхности цилиндра равна 90π см 2 .
6. Найдите радиус основания цилиндра, если площадь осевого сечения цилиндра равна 64 дм 2 , а высота цилиндра 16 дм.
7. Радиус основания цилиндра 1,5 см, а высота – 4 см. Чему равна диагональ осевого сечения?
8. Осевое сечения цилиндра квадрат, площадь которого 36 дм 2 . Чему равна площадь основания цилиндра?
9. Квадрат со стороной 4 см вращается вокруг одной из своих сторон. Чему равна площадь основания полученного тела?
10. Высота цилиндра 8 см, радиус основания 1 см. Чему равна площадь осевого сечения?
11. В равностороннем цилиндре радиус основания равен 7,5 см. Чему равна площадь осевого сечения?
12. Определите площадь боковой поверхности равностороннего цилиндра, высота которого 8 см.
13. Площадь боковой поверхности 75π см 2 . Найдите площадь его полной поверхности, если радиус основания равен 5 см.
14. Чему равна площадь развёртки боковой поверхности цилиндра, радиус основания которого 2 см, а высота- 10 см?
15. Какова площадь боковой поверхности равностороннего цилиндра с радиусом основания 5 см?
Читайте также: Что такое цилиндр выключения сцепления
16. Высота цилиндра 20 см, радиус основания 10 см. Найдите площадь сечения, проведённого параллельно оси цилиндра на расстоянии 6 см от неё.
17. Высота цилиндра – 12 см, радиус основания – 7 см. Цилиндр пересечён плоскостью так, что в сечении оказался квадрат. Найдите расстояние от сечения до оси.
Тестовые вопросы к теме «Цилиндр»
1. Диагональ осевого сечения цилиндра равна см, а радиус основания – 3 см. Найдите высоту цилиндра.
а) см; б) 12 см; в) 5 см; г) см;
2. Площадь осевого сечения равностороннего цилиндра равна 4 см². Найдите площадь основания цилиндра.
а) 2π см²; б) π см²; в) 4π см²; г) 0,5π см²;
3. Радиус цилиндра равен х, его высота – 2, площадь боковой поверхности равна у, площадь полной поверхности – 2у. Найдите х и у.
а) х = 2, у = 8π; б) х = 1, у = 4π; в) х = 2, у = 8;
г) х = 6, у = 24; д) х = 4, у = 16π
4. Диагональ сечения цилиндра, параллельного оси, равна 8√3, она наклонена к плоскости основания под углом 60°. Это сечение в основании отсекает дугу в 120°. Найдите площадь осевого сечения цилиндра.
а) определить нельзя; б) 48; в) 16√3; г) 96√3;
5. Выберите верное утверждение.
а) Длина образующей цилиндра называется радиусом цилиндра;
б) цилиндрическая поверхность называется боковой поверхностью цилиндра;
в) сечение цилиндра, перпендикулярное оси цилиндра, называется осевым;
г) площадь боковой поверхности цилиндра вычисляется по формуле ;
д) цилиндр может быть получен в результате вращения треугольника вокруг одной из сторон.
6. Сечение проведено параллельно оси цилиндра и отстает от нее на расстояние, равное 3. Найдите площадь сечения, если радиус цилиндра равен 5, а его высота равна 10.
а) 40; б) 80; в) 60; г) 30; д)
7. Сколько понадобится краски, чтобы покрасить бак цилиндрической формы с крышкой, имеющий диаметр основания 1,25 м и высоту 1,44 м, если на один квадратный метр расходуется 0,25 кг краски (найдите с точностью до 0,1 кг)?
а) 2,0 кг; б) 2,1 кг; в) 2 кг; г) 1,9 кг; д) 2,03 кг.
8. Развертка боковой поверхности цилиндра – квадрат со стороной 1. Найдите площадь полной поверхности цилиндра с точностью до 0,001.
а) 7,283; б) 0,159; в) 1,318; г) 1,159; д) 0,318.
9. Основанием прямой призмы служит треугольник со сторонами 6, 8 и 10. Высота призмы равна 4. Найдите площадь боковой поверхности описанного около призмы цилиндра.
а) 40π; б) 40 ; в) 32π; г) 20π; д) 32.
10. Радиус r основания цилиндра в3 раза меньше его высоты h . Площадь полной поверхности цилиндра равна 288π см². Найдите r и h .
а) r = 18 c м, h = 6 c м; б) r = 6 см, h = 18 см; в) r = 2 см, h = 6 см;
г) определить нельзя; д) r = 12 см, h = 36 см.
1. Диагональ осевого сечения цилиндра равна см, а высота – 5 см. Найдите радиус цилиндра.
а) см; б) 8 см; в) 4 см; г) см;
2. Площадь основания равностороннего цилиндра равна 2π см². Найдите площадь осевого сечения цилиндра.
а) 8π см²; б) 8 см²; в) 2 см²; г) 4 см²; д) определить нельзя.
3. Радиус цилиндра равен 2, его высота – х, площадь боковой поверхности равна у, площадь полной поверхности равна 2у. Найдите х и у.
а) х = 2, у = 8π; б) х = 1, у = 4π; в) х = 2, у = 8; г) х = 6, у = 24; д) х = 4, у = 16π
4. Сечения цилиндра плоскостью, параллельное оси, удалено от нее на √3. Это сечение отсекает в основании дугу в 60°. Найдите площадь осевого сечения цилиндра, если площадь данного сечения равна 8.
а) определить нельзя; б) 8; в) 16√3; г) 8√3; д) 16.
5. Выберите верное утверждение.
а) Радиус цилиндра не может равняться высоте цилиндра;
б) площадь боковой поверхности цилиндра равна произведению площади основания цилиндра на его высоту;
в) сечение цилиндра, параллельное оси цилиндра, называется осевым;
г) площадь полной поверхности цилиндра вычисляется по формуле ;
д) цилиндр может быть получен в результате вращения прямоугольника вокруг одной из его сторон.
6. В цилиндре параллельно его оси проведено сечение. Диагональ сечения, равная 16, составляет угол 60° с плоскостью основания. Радиус основания цилиндра равен 5. Найдите расстояние от оси цилиндра до плоскости сечения.
а) 3; б) 4; в) 8; г) 5; д)
7. Сколько понадобится краски, чтобы покрасить бак цилиндрической формы с крышкой, имеющий диаметр основания 1,44 м и высоту 1,25 м, если на один квадратный метр расходуется 0,25 кг краски (найдите с точностью до 0,1 кг)?
а) 2,0 кг; б) 2,2 кг; в) 2,3 кг; г) 2,1 кг; д) 2,23 кг.
8. Развертка боковой поверхности цилиндра – квадрат со стороной 2. Найдите площадь полной поверхности цилиндра с точностью до 0,001.
а) 5,141; б) 0,159; в) 4,637; г) 2,159; д) 0,318.
9. Основанием прямого параллелепипеда служит ромб со стороной, равной 4, и углом 60°. Высота параллелепипеда равна 5. Найдите площадь боковой поверхности вписанного в параллелепипед цилиндра.
а) 20π√3; б) 10√3; в) 10π; г) 20π; д) 10π√3.
10. Площадь боковой поверхности цилиндра вдвое больше площади основания, а площадь полной поверхности равна 256π см². Найдите радиус r и высоту цилиндра h .
а) r = 8 c м, h = 6 c м; б) r = 6 см, h = 6 см; в) r = 6 см, h = 8 см;
г) r = 8 см, h = 8 см. д) определить нельзя.
📹 Видео
№522. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующейСкачать
№538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевогоСкачать

№523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высотуСкачать

№525. Площадь осевого сечения цилиндра равна 10 м2, а площадь основания — 5 м2.Скачать

11 класс, 15 урок, Площадь поверхности цилиндраСкачать

11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Геометрия В равносторонний конус (диаметр основания конуса равен длине его образующей) вписан шарСкачать

Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

Все типы 3 задания ЕГЭ математика профиль 2024Скачать

РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

ЦилиндрСкачать

ЦИЛИНДР геометрия егэ по математике профильный уровень ЯщенкоСкачать

№550. Осевое сечение конуса — прямоугольный треугольник. Найдите площадь этого сечения, еслиСкачать

№551. Осевое сечение конуса — правильный треугольник со стороной 2г. Найдите площадь сечения,Скачать

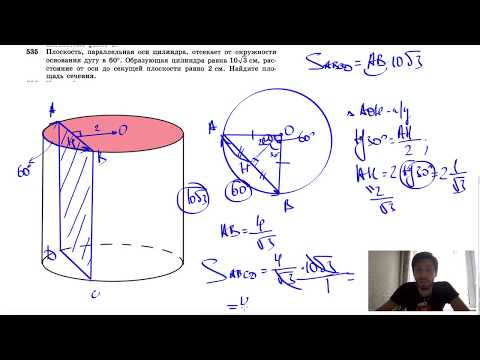
№535. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 60Скачать
Тема 4. Цилиндр. Осевое сечение цилиндра. Развертка боковой поверхности цилиндра. Площадь боковойСкачать

14 ноября 11 классСкачать

КОНУС егэ по геометрии профильный уровень егэ по математикеСкачать



















