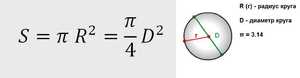Длина окружности поперечного сечения цилиндра что это (7 видео)

Колумнист газеты The Guardian Алекс Беллос опубликовал сегодня задание из выпускного экзамена по математике, вошедшего в экзаменационные материалы 16 стран. Как пишет Беллос, правильно решают эту задачку только 10% экзаменуемых (в Швеции почему-то целых 24%). При этом для того, чтобы решить её, нужно владеть только той математикой, которую осваивают до восьмого класса обычной средней школы.

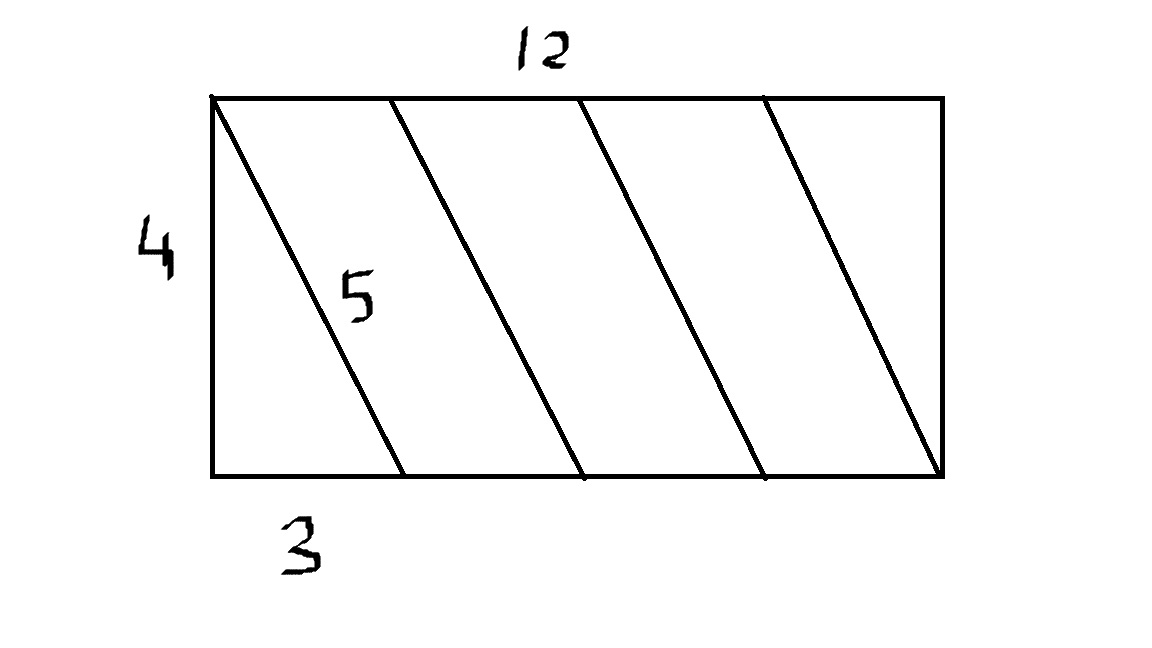
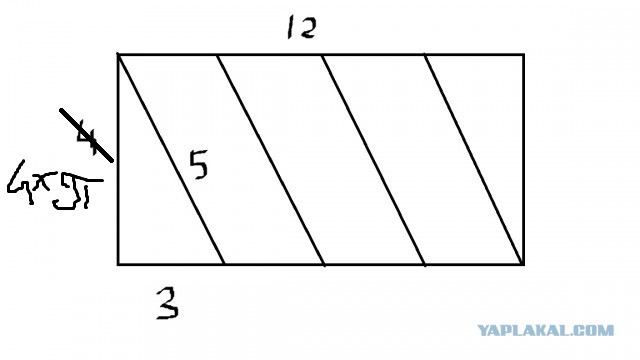
Дано: цилиндр, на которой очень аккуратно и ровно накручена проволока. Проволоки хватило ровно на четыре оборота вокруг цилиндра. Длина цилиндра — 12 сантиметров, длина окружности поперечного сечения — 4 сантиметра. Найдите длину проволоки.

Разверни цилиндр в плоскость и посчитай по теореме пифагора (катеты и гипотенузы).

Только ты цилиндр не развернул, у тебя по прежнему диаметр на рисунке, а должна быть длина окружности.

Очевидно что квадратный корень из суммы квадратов 12 и 4*4, т.е. 20 сантиметров.

Зашибись в 16 странах экзамены. Я поражен сложностью проблемы.

Цитата (maxxxak @ 6.06.2017 — 09:35)

Цитата (ВилийПупкин @ 6.06.2017 — 07:33)

20см

С чего вдруг? Представь что это не проволока, а линия нарисованная синим фломастером, суть задачи не меняется.

Цитата

правильно решают эту задачку только 10% экзаменуемых (в Швеции почему-то целых 24%)

Шведы эту задачу на уроках решают?

Цитата (печник99 @ 6.06.2017 — 09:41)

теперь ты не ВилийПупкин, а ВеликийПупкин!

У меня батарейки в клавиатуре садились когда я на ЯПе регистрировался, поэтому пара букв и пробел не пропечатались ?

Цитата (justwant @ 6.06.2017 — 07:28)

длина окружности поперечного сечения — 4 сантиметра

Они там совсем пизданулись? У нас никогда не было задач, где сразу длина окружности давалась. Давали диаметр, а там дальше сам ебись Пи*Дэ.

имхо, в условии не сказано, что проволока намотана по всей длине цилиндра. говорится только, что очень аккуратно и ровно.
рисунок же сбивает с толку, но неизвестно, имеется ли этот рисунок в оригинале этой задачи.

возможно, что проволока намотана не таким (\\\\) образом, а таким (||||)
тогда просто достаточно будет умножить длину окружности на 4 и получим итоговую длину проволоки

Цитата (justwant @ 6.06.2017 — 07:28)

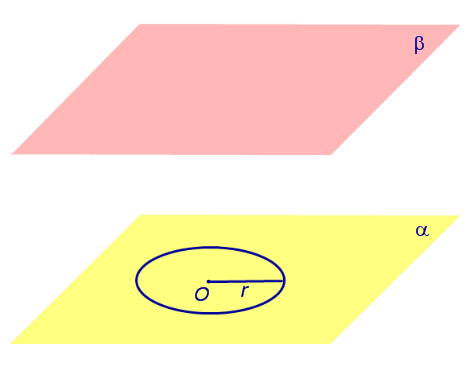
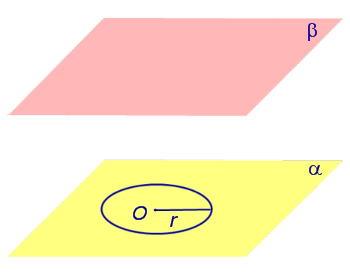
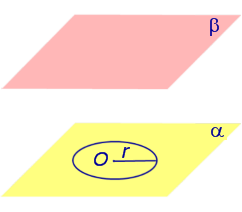
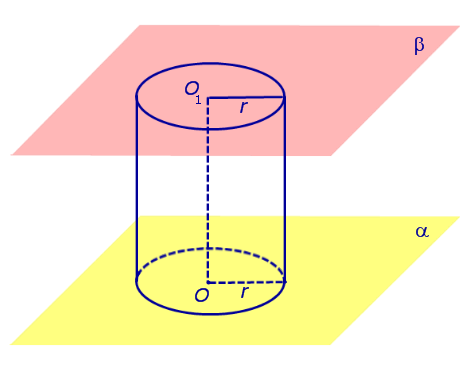
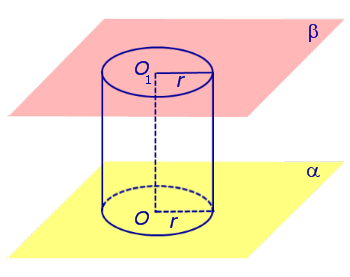
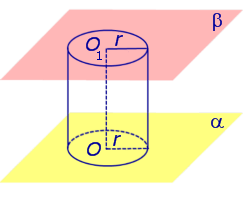
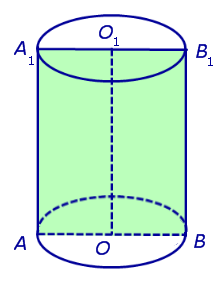
потратил на задачу 3 минуты, из них 2 — искал ручку и листочек. Прочитал бы задачу сразу внимательно, не пошел бы за бумагой, в уме решается.

Моя самооценка повысилась! Вообще не тянет на выпускной экзамен. наверное опять на обманули.

элементарно длина диагонали квадрата 12×16 см (или гипотенуза треугольника с соответствующими катетами)

учтите что в условии уже указана длина окружности а не диаметр — 4 витка по 4 см.

Эх вы, пифагоры античные. Современные компьютерные ~~лентяи~~ школьники всегда должны решать общий случай, чтобы второй раз думать не пришлось!
Длина развёрнутой пружины равна количество витков, умноженное на длину окружности, поделённое на косинус угла витка.
.
Подставляем, получаем = 20 и идём дальше пьянствовать. Делов-то.

псы. в нашем случае длину окружности и вычислять не пришлось. Обычно известен диаметр. Тогда подставляем D*PI.

Содержание

Цилиндры
Основные определения и свойства цилиндра
Сечения цилиндра
Объем цилиндра. Площадь боковой поверхности цилиндра. Площадь полной поверхности цилиндра
Расчет площади поперечного сечения круга
Определение величины
Область применения
Способы расчета
🎥 Видео

Видео:Длина окружности. Математика 6 класс.Скачать

Цилиндры

Видео:Объём цилиндраСкачать

Основные определения и свойства цилиндра

Если из каждой точки окружности опустить перпендикуляр на плоскость β , то основания этих перпендикуляров образуют на плоскости β окружность радиуса r , центр O₁ которой является основанием перпендикуляра, опущенного из точки O на плоскость β (рис.2).

Отрезок перпендикуляра, опущенного из любой точки окружности с центром O на плоскость β , который заключен между плоскостями α и β , называют образующей цилиндра .

Совокупность всех образующих цилиндра называют цилиндрической поверхностью .

Фигуру, ограниченную цилиндрической поверхностью и плоскостями α и β, называют цилиндром .

Отрезок OO₁ называют осью цилиндра .

Радиус окружности Радиус окружности на плоскости α с центром в точке O называют радиусом цилиндра .

Круги с центрами O и O₁ на плоскостях α и β , называют основаниями цилиндра .

Замечание 1. Цилиндрическую поверхность часто называют боковой поверхностью цилиндра . Боковая поверхность цилиндра и основания цилиндра вместе составляют полную поверхность цилиндра .

Замечание 2. Каждая образующая цилиндра параллельна оси цилиндра, а длина каждой образующей цилиндра равна высоте цилиндра.

Замечание 3. Прямая OO₁ является осью симметрии цилиндра, а середина отрезка OO₁ является центром симметрии цилиндра.

Видео:Цилиндр - расчёт площади, объёма.Скачать

Сечения цилиндра

Определение 2. Сечением цилиндра называют пересечение цилиндра с плоскостью.
Если сечение проходит через ось цилиндра, то такое сечение называют осевым сечением цилиндра (рис. 3).

На рисунке 3 изображено одно из осевых сечений цилиндра – прямоугольник AA₁B₁B .

Замечание 4. Каждое осевое сечение цилиндра с радиусом r и высотой h является прямоугольником со сторонами 2r и h .

Определение 3. Перпендикулярным сечением цилиндра называют сечение, перпендикулярное оси цилиндра (рис. 4).

Замечание 5. Любым перпендикулярным сечением цилиндра будет круг радиуса r .

Замечание 6. Более подробно случаи взаимного расположения цилиндра и плоскости рассматриваются в разделе нашего справочника «Взаимное расположение цилиндра и плоскости в пространстве».

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Объем цилиндра. Площадь боковой поверхности цилиндра.
Площадь полной поверхности цилиндра

Для цилиндра с радиусом r и высотой h (рис. 5)

введем следующие обозначения

V	объем цилиндра
S_бок	площадь боковой поверхности цилиндра
S_полн	площадь полной поверхности цилиндра
S_осн	площадь основания цилиндра

Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности цилиндра:

при помощи предельного перехода, когда число сторон правильной призмы n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Расчет площади поперечного сечения круга

В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.

Видео:Лучший способ найти площадь кругаСкачать

Определение величины

Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.

По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.

На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».

С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.

Видео:Видеоурок по математике "Цилиндр"Скачать

Область применения

Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:

Определение объемов емкостей.
Решение задач по сопротивлению материалов и электротехнике.
Расчет количества материалов при проектировании, строительстве и ремонте.
Ведение поливного земледелия.

Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.

Круг имеет ряд характеристик:

радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
длина окружности (C/c/L/l).

Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Способы расчета

Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.

Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.

При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.

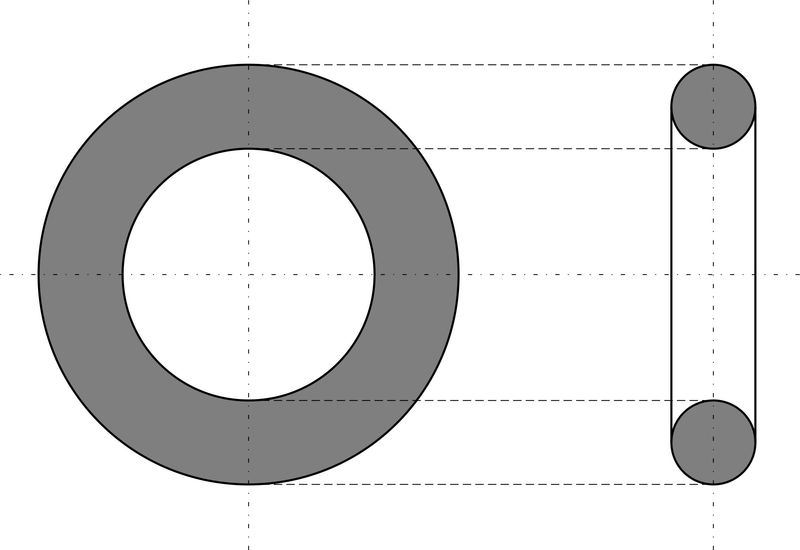
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).

Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:

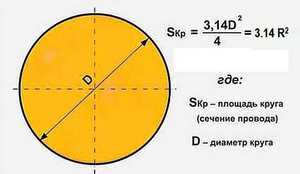
Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.

Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».