- Длинный цилиндр радиуса а заряженный равномерно по поверхности вращается
- Длинный цилиндр радиуса а заряженный равномерно по поверхности вращается
- Чемпионы рейтинга экспертов в этой рассылке
- / НАУКА И ОБРАЗОВАНИЕ / Точные и естественные науки / Физика
- Задать вопрос экспертам этой рассылки »
- Скажите «спасибо» эксперту, который помог Вам!
- Жорина Л., Черноуцан А.И. Решение задач с распределенной силой // Квант
- 💥 Видео
Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Длинный цилиндр радиуса а заряженный равномерно по поверхности вращается
2018-05-14
Длинный цилиндр радиуса $a$, заряженный равномерно по поверхности, вращается вокруг своей оси с угловой скоростью со. Найти энергию магнитного поля, приходящуюся на единицу длины цилиндра, если линейная плотность заряда цилиндра равна $\lambda$ и $\mu = 1$.
Когда цилиндр с линейной плотностью заряда $\lambda$ вращается с круговой частотой $\omega$, плотность поверхностного тока (заряд / длина $\times$ время) $i = \frac $.
Направление поверхностного тока является нормальным к плоскости рисунка при $Q$, а вклад этого тока в магнитное поле в P равно
где $\vec $ — направление тока. По величине, $| \vec \times \vec | = r$, так как $\vec $ нормаль к $\vec $, а направление $d \vec$, показано на рис.
Это компонент, $d \vec_ $ исчезает из-за цилиндрической симметрии. Компонент, который остается,
где мы использовали $\frac > = d \Omega$ и $\int d \Omega = 4 \pi$, общий телесный угол около любой точки
Магнитное поле обращается в нуль вне цилиндра. Полная энергия на единицу длины цилиндра равно,
Видео:Цилиндр крутится - вихревое электрическое поле мутится? | Олимп | Дикая ботва №2Скачать

Длинный цилиндр радиуса а заряженный равномерно по поверхности вращается
Хостинг портала RFpro.ru:
Московский хостер
Профессиональный платный хостинг на базе Windows 2008
Чемпионы рейтинга экспертов в этой рассылке
/ НАУКА И ОБРАЗОВАНИЕ / Точные и естественные науки / Физика
| Номер выпуска: | 877 |
| Дата выхода: | 26.11.2009, 02:00 |
| Администратор рассылки: | Химик CH , Модератор |
| Подписчиков / экспертов: | 239 / 98 |
| Вопросов / ответов: | 1 / 3 |
Вопрос № 174397: Доброго всем времени суток. Прошу помочь с решением следующих задач. Желательно срочно. =) 1. Полубесконечный круглый цилиндр радиуса R заряжен равномерно по поверхности так, что на единицу его длины приходится заряд λ. Найти напряженно. Вопрос № 174397:
Доброго всем времени суток. Прошу помочь с решением следующих задач. Желательно срочно. =)
1. Полубесконечный круглый цилиндр радиуса R заряжен равномерно по поверхности так, что на единицу его длины приходится заряд λ. Найти напряженность электрического поля в центре основания цилиндра.
2. На катоде электролитической ванны выделилось m меди. Определите, какое понадобилось для этого время. Известно, что ток через электроды ванной возрастал линейно от I0 до I1.
Отправлен: 21.11.2009, 01:37
Вопрос задал: D1ver , Посетитель
Всего ответов: 3
Страница вопроса » Отвечает Shvetski , Специалист :
Здравствуйте, D1ver.
2.
Дано:
Медь, для меди известны: Молярная масса M (63,5*10 -3 кг/моль)и валентность z(может быть 1 или 2).
m — масса меди
Токи I0 и I1
Найти: t
Решение:
Согласно первому закону Фарадея для электролиза масса вещества, выделяющаяся на катоде, пропорциональна прошедшему заряду
т.е.
m=k*q=k*(I0+I1)*t/2 (1) (поскольку ток возрастал линейно, среднее значение силы тока I=(I0+I1)/2)
Согласно второму закону Фарадея электрохимический эквивалент
k= (1/F)*(M/z) (2), F=9.65*10 4 Кл/моль — постоянная Фарадея)
Сопоставив выражения (1) и (2) выразим время t
Ответ отправил: Shvetski , Специалист
Ответ отправлен: 21.11.2009, 02:27
Оценка ответа: 5
Комментарий к оценке:
Спасибо за быстрое решение одной из задач ?
| Как сказать этому эксперту «спасибо»? |
| Отправить SMS#thank 256752 на номер 1151 (Россия) | Еще номера » |
| Вам помогли? Пожалуйста, поблагодарите эксперта за это! |
Отвечает Попов Владимир Иванович , Студент :
Здравствуйте, D1ver.
Задача 1.
Для решения вашей задачи выберем на поверхности заряженного цилиндра бесконечно малый участок. Обозначим его площадь как dS. Примем также бесконечно малое смещение вдоль оси цилиндра за dZ, а бесконечно малую дугу окружности произвольного поперечного сечения за dL.
Тогда dS = dL*dZ.
Далее обозначим отрезок, соединяющий выбранный участок с серединой основания цилиндра как (r), угол, который образует этот отрезок с осью цилиндра как (b), а угол поворота радиуса поперечного сечения, проходящего через наш участок как (а).
Тогда r = R / sin(b); dL = R*da; dZ = r*db.
Ошибка! Данное выражение даёт длину отрезка, перпендикулярного отрезку r, тем временем, как отрезок образующей dZ параллелен оси и составляет с отрезком r угол b, следовательно dZ = r*db/sin(b).
Соответственно, последующие вычисления также содержат указанную ошибку
Рассчитаем напряженность поля, создаваемого в заданной точке зарядом dq, сосредоточенным в пределах площадки dS:
dE = dq / (4*pi*e0*r^2) = sigma*dS / (4*pi*e0*r^2), где sigma — поврехностная плотность заряда.
Поскольку sigma = tau / (2*pi*R), то:
dE = tau*dS / (8*pi^2*e0*R*r^2) = tau*dL*dZ / (8*pi^2*e0*R*r^2) = tau*R*da*r*db / (8*pi^2*e0*R*r^2) = tau*da*db / (8*pi^2*e0*r) = tau*da*db / (8*pi^2*e0*(R/sin(b))) = tau*da*sin(b)*db / (8*pi^2*e0*R).
В силу принципа суперпозиции и с учётом осевой симметрии, все поперечные относительно оси цилиндра составляющие напряжённости поля от всех подобных выбранному участков dS в сумме дают 0, а продольные в проеции на ось симметри — интеграл:
Ez = Int[dE*cos(b)] = Int[tau*da*sin(b)*cos(b)*db / (8*pi^2*e0*R)] = Int[2*tau*da*sin(b)*cos(b)*db / (16*pi^2*e0*R)] = Int[tau*da*sin(2b)*db / (16*pi^2*e0*R)].
Подставляя пределы интегрирования по (а) от 0 до 2pi, по (b) — от (pi/2) до 0, получим: Ez = (tau*2pi/(16*pi^2*e0*R))*(-cos(2b)/2)|
= — tau / (8*pi*e0*R), с учётом знака проекции (вектор напряжённости поля будет направлен в сторону, противоположную направлению оси цилиндра).
Таким образом, окночательно имеем ответ: E = tau / (8*pi*e0*R).
Проверка соответствия единиц измерения:
[E] = (Кл/м) / ((Ф/м)*м) = Кл / (м*Ф) = Кл / (м*Кл/В) = Кл*В / (м*Кл) = В / м.
Задача 2.
В соответствии с первым законом электролиза, для бесконечно малого промежутка времени dt на электродах выделится масса вещества dm, равная произведению электрохимического эквивалента этого вещества k на количество прошедшего за этот промежуток времени через электролит заряда dq:
dm = k*dq.
Учитывая, что dq = i*dt, где i — сила тока, проходящего через электролит в данный момент времени, получаем:
dm = k*i*dt.
По условию задачи, ток нарастает линейно. Обозначим коэфициент пропорциональности в линейной зависимости силы тока от времени через В, тогда:
i = I0 + B*t.
Поскольку задано конечное значение силы тока I1, то:
I1 = I0 + B*t1; тогда B = (I1 — I0) / t1.
Окончательно, диффренциальное уравнение электролиза запишется в виде:
dm = k*(I0 + B*t)*dt.
Интегрируя это уравнение по массе от 0 до m, по времени — от 0 до t1, получим:
m = k*I0*t1 + k*B*t1^2 / 2,
m = k*I0*t1 + k*((I1 — I0) / t1)*t1*2 / 2,
2m = 2*k*I0*t1 + k*(I1 — I0)*t1,
2m = t1*k*(2*I0 + I1 — I0),
2m = t1*k*(I0 + I1),
t1 = 2m / (k*(I0 + I1)).
Проверка соответствия единиц:
[t1] = кг / ((кг/Кл)*А) = Кл / А = Кл / (Кл/с) = с.
Успеха. Удачи при сдаче.
Ответ отправил: Попов Владимир Иванович , Студент
Ответ отправлен: 22.11.2009, 13:21
| Как сказать этому эксперту «спасибо»? |
| Отправить SMS#thank 256803 на номер 1151 (Россия) | Еще номера » |
| Вам помогли? Пожалуйста, поблагодарите эксперта за это! |
Отвечает Химик CH , Модератор :
Здравствуйте, D1ver.
Рассмотрим кольцо (отрезок длины цилиндра) шириной dl.
Оно несёт заряд dq=λ*dl.
Пусть направление от центра основания на кольцо составляет с радиусом основания угол φ.
Тогда расстояние от центра основания до точек кольца r=R/cosφ
C учётом суперпозиции (вертикальные составляющие складываются, горизонтальные нейтральзуются) получаем напряжённость
dE=k*dq*sinφ/r 2 =k*λ*dl*sinφ*cos 2 φ/R 2
пусть ширина кольца видна из центра основания под углом dφ
Тогда его ширина dl=r*dφ/cosφ=R*dφ/cos 2 φ
подставляем в выражение напряжённости
dE=k*λ*(R*dφ/cos 2 φ)*sinφ*cos 2 φ/R 2 =k*λ*sinφ*dφ/R
интегрируем от 0 до п/2
E=0 п/2 ∫k*λ*sinφ/R dφ=k*λ/R*(cos(п/2)-cos0)=-k*λ/R=-λ/(4*п*ε0*R)
——
Никогда не просите у химика просто СОЛЬ.
Ответ отправил: Химик CH , Модератор
Ответ отправлен: 22.11.2009, 16:50
Латвия, Рига
Тел.: +37128295428
Абонент Skype: himik_c2h5oh
| Как сказать этому эксперту «спасибо»? |
| Отправить SMS#thank 256809 на номер 1151 (Россия) | Еще номера » |
| Вам помогли? Пожалуйста, поблагодарите эксперта за это! |
Оценить выпуск »
Нам очень важно Ваше мнение об этом выпуске рассылки!
Задать вопрос экспертам этой рассылки »
Скажите «спасибо» эксперту, который помог Вам!
* Стоимость одного СМС-сообщения от 7.15 руб. и зависит от оператора сотовой связи. ( полный список тарифов )
** При ошибочном вводе номера ответа или текста #thank услуга считается оказанной, денежные средства не возвращаются.
*** Сумма выплаты эксперту-автору ответа расчитывается из суммы перечислений на портал от биллинговой компании.
Видео:Урок 224. Напряженность поля неточечных зарядовСкачать

Жорина Л., Черноуцан А.И. Решение задач с распределенной силой // Квант
Жорина Л., Черноуцан А.И. Решение задач с распределенной силой // Квант. — 2004. — № 6. — С. 36-38.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
При решении задач из различных разделов физики приходится встречаться с ситуациями, когда силы непрерывно распределены вдоль какой-нибудь линии или поверхности. Обычно требуется найти или равнодействующую этих сил, или возникающие в объекте их приложения (линейном или плоском) натяжения и деформации.
При решении таких задач удобно использовать один из двух подходов. В первом подходе — назовем его дифференциальным — анализируют силы, действующие на маленький элемент линии или поверхности, при этом размер этого элемента в окончательный ответ не входит. Во втором — инmегральном — подходе производят суммирование по всем элементам, опираясь при этом на симметрию системы и стараясь избежать прямого интегрирования. Впрочем, как мы увидим, эти подходы тесно друг с другом связаны.
Начнем с рассмотрения линейных объектов.
Задача 1. Точечный заряд q находится в центре кольца радиусом R, по которому равномерно распределен одноименный заряд Q. Найдите силу натяжения кольца. Взаимодействие зарядов кольца друг с другом не учитывать.
Разберем два способа решения этой задачи.
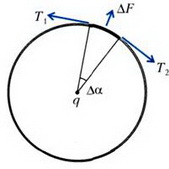
Способ 1. Запишем условие равновесия элемента кольца, видного из центра под маленьким углом Δα (рис. 1).
Заряд этого элемента равен , на него действует сила отталкивания от заряда qи две одинаковые по модулю силы натяжения и (T1 = T2 = Τ), угол между которыми равен . Равнодействующая сил натяжения (с учетом малости Δα) составляет , и условие равновесия этого элемента принимает вид
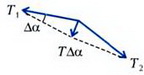
Способ 2. Рассмотрим силы, приложенные к полукольцу (рис. 2).
На него действуют две параллельные силы натяжения. Их сумма, равная 2T, уравновешивается равнодействующей всех электростатических сил, приложенных к различным элементам полукольца. Из симметрии системы очевидно, что равнодействующая электростатических сил направлена по оси у. Получаем
Смысл приведенного расчета состоит в следующем: вместо того чтобы брать проекцию силы, приложенной к элементу кольца, на ось у, мы заменили этот элемент его проекцией на ось х: . Мы как бы «выпрямили» полуокружность, после чего все силы стали параллельны друг другу. Отметим, что, в соответствии с третьим законом Ньютона, мы одновременно вычислили силу, действующую на точечный заряд qсо стороны полукольца, т.е. нашли напряженность поля, создаваемую полукольцом с зарядом в своем центре:
На первый взгляд, второй способ решения выглядит более громоздким и искусственным. Однако в некоторых случаях, особенно при вычислении равнодействующей силы, он имеет определенные преимущества.
Задача 2. Плоский контур расположен в однородном магнитном поле с индукцией В перпендикулярно линиям индукции. По контуру течет ток силой I. Найдите натяжение провода контура в двух случаях: а) контур имеет форму окружности радиусом R; б) контур имеет форму эллипса с полуосями a и b. Во втором случае следует найти натяжение в точках пересечения эллипса с осями. Силой магнитного взаимодействия частей контура пренебречь.
Первый случай очень похож на задачу 1, и его можно решать любым из двух способов. При решении первым способом получаем уравнение, связывающее силу натяжения провода с магнитной силой (силой Ампера), действующей на контур со стороны магнитного поля:
Однако ясно, что такое решение не применимо к контуру в форме эллипса. Что же касается второго подхода, то он применим как в первом, так и во втором случаях.
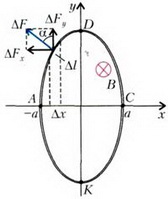
Чтобы найти натяжение провода в точках А и С эллипса (рис. 3), надо вычислить магнитную силу , действующую на примыкающую к этим точкам половину эллипса.
Проекции этой силы на оси x и yравны, соответственно,
Поскольку магнитная сила равна двум силам натяжения, получаем
Аналогично найдем натяжение провода в точках D и К:
Можно заметить, что такой же расчет применим к участку контура любой формы. Сформулируем утверждение: сила, действующая со стороны однородного магнитного поля на участок контура с током любой формы, соединяющий какие-то две точки, равна силе, действующей на соединяющий эти точки прямой провод с таким же током. Физический смысл этого утверждения состоит в том, что полная сила, действующая на замкнутый контур с током со стороны однородного магнитного поля, должна быть равна нулю (иначе бы нарушался закон сохранения энергии).
Задача 3. Тонкое кольцо массой m и радиусом R вращается вокруг своей оси с угловой скоростью ω. Найдите натяжение кольца.
Запишем второй закон Ньютона для малого элемента кольца. Равнодействующая двух сил натяжения сообщает этому элементу центростремительное ускорение:
Это решение аналогично первому, т.е. дифференциальному, подходу в статических задачах. А применим ли в этом случае интегральный подход? Если мы запишем второй закон Ньютона для половины кольца, то в формулу для центростремительного ускорения центра масс полукольца войдет расстояние rц от центра масс до оси:
Если бы мы знали rц, то нашли бы натяжение Τ вторым способом. Однако можно использовать это уравнение именно для вычисления rц: подставив сюда T, вычисленное первым способом, получим
Задача 4. Тонкое алюминиевое кольцо радиусом R = 10 см вращается вокруг своей оси. При какой угловой скорости кольцо разорвется, если разрыв происходит при механическом напряжении σκρ = 2•10 7 Н/м 2 . Плотность алюминия ρ = 2700 кг/м 3 .
Условие разрыва кольца запишем в виде
где Τ — натяжение кольца, S — площадь сечения. Подставим Τ из решения предыдущей задачи и учтем, что .
Интересно, что ответ не зависит от толщины кольца.
Перейдем теперь к рассмотрению не линейных, а плоских объектов. Обычно в этих задачах удобнее применять второй (интегральный) подход. Однако попробуйте самостоятельно решить их и с помощью дифференциального метода.
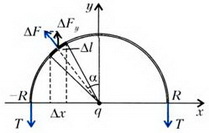
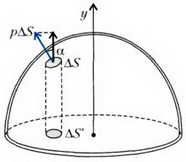
Задача 5. Внутри тонкой сферы радиусом R создано избыточное давление р. Какой должна быть толщина сферы, чтобы она при этом не разорвалась, если разрыв происходит при напряжении σκρ?
Из условия равновесия полусферы следует, что сила упругости в диаметральном сечении равна равнодействующей сил давления:
Для вычисления равнодействующей сил давления отметим, что она направлена вдоль оси симметрии полусферы (рис. 4):
Как и в задачах 1 и 2, мы, вместо того чтобы проецировать силу на ось симметрии, взяли проекцию площади площадки ΔS на плоскость, на которую опирается полусфера (т.е. как бы «выпрямили» полусферу). Подставив в предыдущую формулу, получим
💥 Видео
Билет №02 "Теорема Гаусса"Скачать

Визуализация гравитацииСкачать

Теорема Гаусса для расчета полей цилиндра (нити) и плоскостиСкачать

3.250 ирСкачать

Электромагнетизм Пр3.4. Теорема Гаусса. Поле бесконечного цилиндра.Скачать

Лекция 1-4 Теорема Гаусса Формулировка и примерыСкачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Как решать задачи на нахождение магнитного поля.Скачать

ВзаимоиндукцияСкачать

Магнитное поле соленоидаСкачать

Физика 8 класс. §57-62. Электромагнитные явленияСкачать

Физика 2 (Электромагнетизм) 6 лекция (12.12.2020)Скачать

Кокшаров Ю. А. - Электромагнетизм - Теорема Остроградского — ГауссаСкачать

Астроитоги 2022Скачать

Лекция №7 "Закон Био-Савара-Лапласа. Соленоидальные поля"Скачать

Магнитное поле на оси цилиндрического магнитаСкачать

Поляков П. А. - Электромагнетизм - Теорема о циркуляции. Электрический дипольСкачать