Цилиндр представляет собой тело, состоящее из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов (Рис.1).
Два круга, лежащих в параллельных плоскостях, называются основаниями цилиндра. Отрезки, соединяющие соответствующие точки окружностей кругов, называются образующими.
Так как основания совмещаются параллельным переносом, то они равны. И так как они лежат в параллельных плоскостях, то образующие цилиндра параллельны и равны.
Если образующие перпендикулярны основанию, то цилиндр называется прямым.
Поверхность цилиндра состоит из двух оснований и боковой поверхности. Боковая поверхность состоит из образующих.
Осью цилиндра называется прямая, проходящая через центры оснований. Радиусом цилиндра называется радиус его основания. А высотой цилиндра называется расстояние между плоскостями его оснований.
- Сечение цилиндра плоскостями
- 2.Конус
- Сечение конуса плоскостями
- 3. Вписанная и описанная призма
- 4.Вписанная и описанная пирамида
- 5. Шар
- Сечение шара плоскостью
- 6. Симметрия шара
- 7. Пример 1
- Пример 2
- Пример 3
- Пример 4
- Пример 5
- Докажите что плоскость параллельная плоскости основания цилиндра
- Докажите что плоскость параллельная плоскости основания цилиндра
- 💥 Видео
Видео:№528. Докажите, что если секущая плоскость параллельна оси цилиндра и расстояние междуСкачать

Сечение цилиндра плоскостями
Если взять сечение цилиндра плоскостью, проходящей по его оси, то получится прямоугольник. (Рис.1) Такое сечение называется осевым. Сечение цилиндра плоскостью, параллельной его оси, также представляет собой прямоугольник. Две его стороны — образующие цилиндра, а две другие стороны — параллельные хорды оснований.
Теорема. Плоскость сечения цилиндра, параллельная его плоскости основания, пересекает его боковую поверхность по окружности, равной окружности основания. (Рис.1.1)
Пусть плоскость α — секущая плоскость, параллельная основанию. Подвергнем плоскость α движению в верх вдоль оси цилиндра. Параллельным переносом совместим плоскость α с плоскостью верхнего основания цилиндра. Таким образом сечение боковой поверхности совпадет с окружностью верхнего основания. Теорема доказана.
Рис. 1.1 Сечения цилиндра плоскостями.
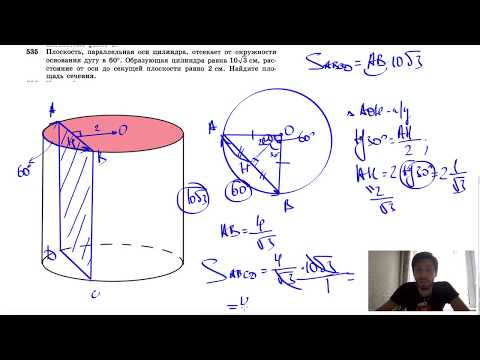
Видео:№535. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 60Скачать
2.Конус
Конусом называется тело, которое состоит из круга — основания конуса, точки, не лежащей в плоскости основания этого конуса — вершины конуса и всех отрезков, соединяющих вершину с точками основания (Рис.2).
Точка, не лежащая в плоскости основания, называется вершиной конуса. Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.
Конус называется прямым, если прямая, проведенная из вершины конуса в центр основания, перпендикулярна плоскости основания.
Высотой конуса называется перпендикуляр, опущенный из вершины конуса на плоскость основания. Осью прямого кругового конуса называется прямая, содержащая его высоту.
Видео:№534. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 120Скачать

Сечение конуса плоскостями
Сечение прямого конуса плоскостью, которая проходит через его вершину, представляет собой равнобедренный треугольник. Боковые стороны этого треугольника являются образующими конуса. Сечение, которое проходит через ось конуса, называется осевым.
Теорема. Сечение конуса плоскостью, параллельной основанию, есть круг с центром на оси конуса.
Доказательство. Пусть α — плоскость, параллельная основанию (Рис 2.1). Плоскость α пересекает конус по кругу. Подвергнем сечение конуса гомотетии относительно вершины конуса. Т.е. совместим плоскость α с плоскостью основания конуса. Сечение конуса полностью совпадет с основанием. Следовательно сечение конуса плоскостью есть круг, а сечение боковой поверхности — окружность с центром на оси конуса.
Видео:ЗАДАНИЕ 8 из ЕГЭ_50Скачать

3. Вписанная и описанная призма
Призма, вписанная в цилиндр, называется призма, у которой плоскости основания совпадают с плоскостями оснований цилиндра, а боковые ребра являются образующими цилиндра.
Читайте также: Снять тормозной цилиндр урал 4320
Призма, описанная около цилиндра, называется призма, у которой плоскости оснований совпадают с плоскостями оснований цилиндра, а боковые грани касаются цилиндра (Рис.3).
Если плоскость проходит через образующую цилиндра и перпендикулярна осевому сечению, то она называется касательной плоскостью к цилиндру.
Рис. 3 Описанная и вписанная призма.
Видео:№521. Докажите, что осевое сечение цилиндра является прямоугольником, две противоположныеСкачать

4.Вписанная и описанная пирамида
Пирамида, вписанная в конус, называется пирамида, у которой вершина совпадает с вершиной конуса, а многоугольник в основании вписан в окружность основания конуса.
Пирамидой, описанной около конуса, называется пирамида, у которой вершина совпадает с вершиной конуса, а в многоугольник основания вписано основание окружности конуса.
Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса (плоскость α) и перпендикулярная плоскости осевого сечения (плоскость β), проходящей через эту образующую (Рис.4).
Рис. 4 Вписанная и описанная пирамида.
Видео:Задание №528 — ГДЗ по геометрии 11 класс (Атанасян Л.С.)Скачать

5. Шар
Шар это геометрическое тело, состоящее из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки. (Рис.5). Точка, от которой все остальные точки находятся на расстоянии не большем данного, называется центром шара.
Граница шара называется сферой. Совокупность всех точек сферы удалена от центра на расстояние, равное радиусу. Таким образом, любой отрезок, соединяющий центр шара с точкой сферы, называется радиусом.
Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром. Концы любого диаметра называются диаметрально противоположными точками шара.
Видео:Задание №603 — ГДЗ по геометрии 11 класс (Атанасян Л.С.)Скачать

Сечение шара плоскостью
Если секущая плоскость проходит через центр шара, например плоскость α, то она называется диаметральной плоскостью. А сечение называется большим кругом (Рис.5.1).
Если секущая плоскость не проходит через центр шара, то в сечении получится также круг. Сформулируем следующую теорему.
Теорема. Любое сечение шара представляет собой круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.
Пусть β — секущая плоскость. Проведем перпендикуляр из центра шара точки O на плоскость β. Обозначим основание перпендикуляра точкой O’.
Рис. 5.1 Сечение шара плоскостью.
Видео:Видеоурок по математике "Цилиндр"Скачать

6. Симметрия шара
Теорема. Центр шара является его центром симметрии, а любая диаметральная плоскость является его плоскостью симметрии.
Доказательство. Пусть α — диаметральна плосксоть шара, а Y его произвольная точка (Рис.6). Построим точку Y’, симметричную точке Y относительно плоскости α. Так как отрезок YY’ перпендикулярен плоскости α и делится этой плоскостью пополам точкой пересечения А, то треугольники OYA и OY’A равны по двум сторонам и углу между ними, т.е. OY=OY’. Отрезки OY и OY’ принадлежат шару, так как OY = OY’ ≤ R.
Отложим отрезок OY» симметрично относительно центра шара точки О. Тогда OY = OY» ≤ R. Т.е. точка Y» также принадлежит шару. Следовательно точка О является точкой симметрии шара, а диаметральная плоскость — плоскостью симметрии.
7. Пример 1
Радиус основания цилиндра 2 м, высота 3 м. Найдите диагональ осевого сечения.
Пусть дан цилиндр высотой 3 м и радиусом 2 м (Рис.7). По теореме Пифагора найдем АС:
AС 2 = AD 2 + CD 2 = 4 2 + 3 2 = 25
Рис.7 Задача. Радиус основания цилиндра 2 м.
Пример 2
Высота цилиндра 6 м, радиус основания 5 м. Концы отрезка DC’, длина которого 10 м, лежат на окружностях оснований. Найдите расстояние от этого отрезка до оси цилиндра.
Пусть дан цилиндр высотой 6 м с радиусом основания 5 м и отрезком DC’ = 10 м (Рис. 8). Проведем два перпендикуляра C’C и D’D. Так как эти перпендикуляры параллельны, то проведем через них плоскость α. Теперь проведем плоскость β через ось O’O, параллельную плоскости α.
Читайте также: Диаметр цилиндров ваз классика
Таким образом, получается, что через две скрещивающиеся прямые OO’ и DC’ проходят две параллельные плоскости α и β. Расстояние между скрещивающимися прямыми равно расстоянию между двумя параллельными плоскостями, в которых эти прямые лежат.
Отсюда следует, что длина перпендикуляра ОЕ и будет расстояние от отрезка DC’ до оси цилиндра OO’.
Найдем хорду DC из прямоугольного треугольника DC’C:
DC 2 = 10 2 — 6 2 = 64, DC = 8 м.
Теперь из прямоугольного треугольника OED найдем ОЕ:
ОЕ 2 = OD 2 — DE 2 = 5 2 — 4 2 = 9
Рис.8 Задача. Высота цилиндра 6 м.
Пример 3
Высота конуса 20 м, радиус основания 25 м. Найдите площадь сечения, проведенного через вершину, если расстояние от него до центра основания конуса равно 12 м.
Пусть дан конус высотой 20 м с радиусом основания 25 м. OF = 12 м (Рис. 9). Найдем синус угла OSF из прямоугольного треугольника OSF.
sin OSF = OF / SO = 12 / 20 = 3/5, следовательно, cos OSF = 4/5
Из прямоугольного треугольника OSC найдем SC:
cos OSC = SO / SC, SC = SO / cos OSC = 20/4/5 = 25 м
По теореме Пифагора найдем ОС:
ОC 2 = SC 2 — SO 2 = 25 2 — 20 2 = 225, OC = 15 м.
Из прямоугольного треугольника АОС найдем АC:
АC 2 = АО 2 — ОС 2 = 25 2 — 15 2 = 400, АC = 20 м.
Таким образм, площадь сечения равна:
SASB = AC * SC = 20 * 25 = 500 м 2 .
Рис.9 Задача. Высота конуса 20 м.
Пример 4
Высота конуса 10 м. Радиус основания 6 м. На каком расстоянии от вершины необходимо провести плоскость, параллельную основанию, чтобы площадь сечения была равна половине площади основания.
Пусть дан конус высотой 10 м и радиусом основания 6 м (Рис. 10). Обозначим площадь основания как Sб, а площадь сечения как Sм. Найдем площадь большего основания Sб:
Sб = π R 2 = π 6 2 = 36π м 2
Соответственно площадь малого основания Sм будет равна:
Sм = Sб / 2 = 36π / 2 = 18π м 2
Отсюда, радиус сечения СА равен
Рассмотрим треугольники BOS и CAS. Они подобны. Коэффициент подобия составляет k = CA / BO = / 6
Отсюда следует, что SA = k SO = 10 

Таким образом, для того чтобы площадь сечения составляла половину площади основания, расстояние от вершины конуса до плоскости сечения должно составлять 5 м.
Рис.10 Задача. Высота конуса 10 м.
Пример 5
Радиусы оснований усеченного конуса 4 м и 12 м, образующая 10 м. Найдите площадь осевого сечения.
Пусть дан усеченный конус. Образующая АС = 10 м и радиусы оснований СЕ = 4 м, АО = 12 м (Рис. 11). Осевое сечение усеченного конуса представляет собой равнобокую трапецию. Отсюда следует, что площадь сечения можно найти как сумму площадей прямоугольника CFTP и двух равных треугольников АСР и TFB.
Найдем площадь двух треугольников АСР и TFB:
По теореме Пифагора найдем СР:
СР 2 = AC 2 — AР 2 = 10 2 — 8 2 = 36, CP = 6 м
SACP + STFP = 2 SACP = 2 * АР * СР / 2 = 2 * 8 * 6 / 2 = 48 м 2
Теперь найдем площадь прямоугольника SCFTP:
SCFTP = CF * CP = 2 CE * CP = 2 * 4 * 6 = 48 м 2
Таким образом, площадь сечения усеченного конуса составляет:
SАCFВ = SCFTP + 2 SACP = 48 + 48 = 96 м 2 .
Читайте также: Из чего состоит мерный цилиндр
Рис.11 Задача. Радиусы оснований усеченного конуса 4 м и 12 м.
Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Докажите что плоскость параллельная плоскости основания цилиндра
· рассмотреть основные виды сечений цилиндра
Время реализации занятия: 45 минут
II Проверка домашнего задания
III Изучение нового материала
Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник (рис. 1, а). Две его стороны — образующие цилиндра, а две другие — параллельные хорды оснований. В частности, прямоугольником является осевое сечение. Это — сечение цилиндра плоскостью, проходящей через его ось (рис. 1, б).
Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.
Пусть β — плоскость, параллельная плоскости основания цилиндра (рис. 2). Параллельный перенос в направлении оси цилиндра, совмещающий плоскость Р с плоскостью основания цилиндра, совмещает сечение боковой поверхности плоскостью Р с окружностью основания. Теорема доказана.
IV Закрепление изученного материала
Осевое сечение цилиндра — квадрат, площадь которого Q. Найдите площадь основания цилиндра.
Сторона квадрата равна IQ . Она равна диаметру основания. Поэтому площадь основания равна:
Видео:Вопросы к § 6 - Геометрия 10-11 класс ПогореловСкачать

Докажите что плоскость параллельная плоскости основания цилиндра
Высота цилиндра равна 5, а радиус основания 10.
а) Докажите, что площадь боковой поверхности цилиндра равна площади его основания.
б) Найдите площадь сечения цилиндра плоскостью, проходящей параллельно оси цилиндра на расстоянии 6 от неё.
а) Вспомним, что площадь боковой поверхности цилиндра вычисляется по формуле , где — радиус основания, — высота цилиндра. В данном случае , поэтому , откуда и следует требуемое.
б) Сечение цилиндра плоскостью, проходящей параллельно его оси OO1, — прямоугольник ABB1A1 (O и AB — соответственно центр и хорда нижнего основания цилиндра), AA1 = 5. Расстояние от оси цилиндра до плоскости сечения равно высоте OH треугольника OAB. OA = OB = 10, OH = 6, откуда
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 2 |
| Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено, или при правильном ответе решение недостаточно обосновано. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
В условии сказано, что дан цилиндр: «Высота цилиндра. «, а в решении рассмотрен прямой цилиндр. Действительно, ответ такой же получится при решении задачи с наклонным цилиндром, но тем не менее, в сечении образуется параллелограмм, а не прямоугольник: прямая АА1 параллельна и равна прямой ВВ1, как образующие, которые параллельны, в свою очередь оси цилиндра — прямой ОО1. По признаку параллельности прямой и плоскости получаем, что ОО1 параллельна плоскости (АА1ВВ1). И уже нельзя говорить, что ОО1 является высотой, ведь цилиндр может быть и наклонным. Прямая ОО1 является осью цилиндра. А условная прямая О1М может являться высотой цилиндра (точка М может совпасть с точкой О, если цилиндр прямой). Она будет являться и высотой параллелограмма (это может быть и прямоугольник, который по определению также является параллелограммом).
Таким образом, ответ хотя и верный, но рассмотрено частное решение данной задачи. Либо составители допустили ошибку не указав, что дан прямой цилиндр (в 2018-ом же писали: «. образующая перпендикулярна плоскости основания»), либо решение данной задачи следует подправить.
В школьном курсе задачи о наклонных цилиндрах не рассматриваются.
💥 Видео
№58. Докажите, что если плоскость γ пересекает одну из параллельных плоскостей α и β,Скачать

Ответы на вопросы к главе 6 - Геометрия 10-11 класс ПогореловСкачать

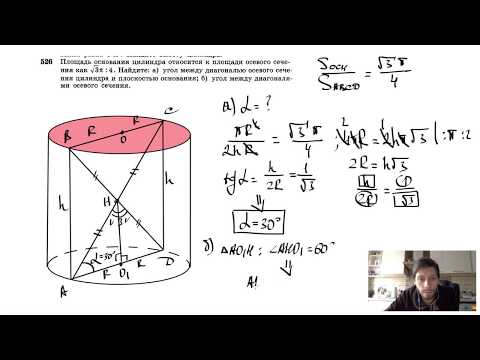
№526. Площадь основания цилиндра относится к площади осевого сечения как √3π:4. Найдите:Скачать
Докажите, что радиус основания цилиндра в 6 раз меньше высоты основания пирамидыСкачать

9 класс, 41 урок, ЦилиндрСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

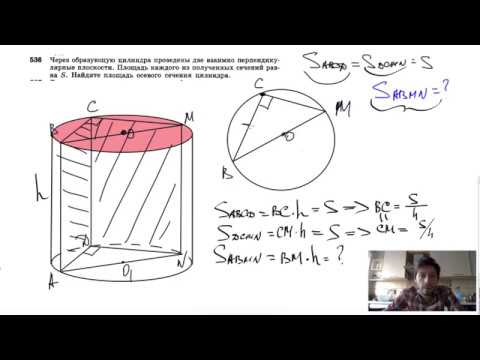
№536. Через образующую цилиндра проведены две взаимно перпендикулярные плоскости.Скачать
№537. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длинеСкачать




















