Два бесконечно длинных коаксиальных цилиндра с радиусами 10 (8 видео)

Содержание

Главная категория => КОНСУЛЬТАЦИИ ПО ВСЕМ ПРЕДМЕТАМ => Тема начата: AdminZiGzag от 10 Октябрь 2010, 17:25:32
Два бесконечно длинных коаксиальных цилиндра с радиусам
Продавец
Описание товара
Дополнительная информация
Отзывы
С товаром «Два бесконечно длинных коаксиальных цилиндра с радиусам» также смотрят:
Политика использования файлов cookie
Что такое cookies?
Какие типы файлов cookie мы используем?
Необходимые файлы cookie
Функциональные файлы cookie
Два бесконечно длинных коаксиальных цилиндра с радиусами 10
Два бесконечно длинных коаксиальных цилиндра с радиусами 10
📺 Видео

Видео:Лекция 2-2 Потенциал - примерыСкачать

Главная категория => КОНСУЛЬТАЦИИ ПО ВСЕМ ПРЕДМЕТАМ => Тема начата: AdminZiGzag от 10 Октябрь 2010, 17:25:32

Условие немного некорректно: если орбиты круговые, то Земля должна находиться в их центре, поэтому окружности — концентрические, а, значит, расстояние между спутниками постоянное. Рассчитать его можно из формулы:
v=(GM/(R+h))^0.5
h=GM/v^2 — R
здесь v — скорость спутника, h — высота над Землёй, G = 6,67*10^(-11) — гравитационная постоянна, M = 6*10^24 кг- масса Земли, R = 6,4*10^6 м- радиус Земли
v1=7600 м/с
v2=7800 м/с
h1=0,53*10^6 м = 530 км
h2=0,18*10^6 м = 180 км
Значит, разница между высотами равна 370 км!

Уточните условие, тогда, возможно, сможем помочь более детально=)

контрольная на заочном.
с физикой на вежливое «Вы». из серии «я Вас не знаю, Вы меня то же»
помогите, пожалуйста.

1. Два бесконечно длинных коаксиальных цилиндра с радиусами R1 = 10 мм и R2 = 20 мм заряжены одноименными зарядами. Поверхностная плотность зарядов на внутреннем цилиндре — d1 = 3,33 нКл/м2, на внешнем цилиндре — d2 = 6,66 нКл/м2. Найти разность потенциалов j1 — j2 между цилиндрами.
2. Какой заряд пройдет по проводнику сопротивлением R = 1 кОм при равномерном нарастании напряжения на его концах от U1 = 15 В до U2 = 25 В в течение Dt = 20 с?
3. Круговой виток, изготовленный из проволоки длиной l = 12,56 см, помещен в однородное магнитное поле индукцией В = 4 мТл. По витку течет ток J = 0,6 А. Нормаль к плоскости витка составляет угол a = 45градусов с направлением линий магнитной индукции. Определить вращающий момент сил М, действующих на виток.
4. Определить фотоэлектрический порог l0(лямбда 0) для металла, если при его облучении фиолетовым светом с длиной волны l(лямбда) = 400 нм максимальная скорость vmax фотоэлектронов равна 0,65 Мм/с.
5. Поток энергии излучения раскаленного металла Ф¢ = 0,67 кВт. Температура поверхности Т = 2500 К, площадь S = 10 см2. Каков был бы поток Ф, если бы эта поверхность была черной?

спасибо большое!
остальные задачи нужно.
но вот позвонить не получится (поправьте, если я ошибаюсь) .
телефон в посте выше — Харьковский? (я из Санкт-Петербурга)

Видимо речь идет о законе колебаний мощности переменного тока.
Первая форму ла — это обащая запись, зависящая от момента времени.
Вторая получается, если подставить время t=T/8 (восьмая чать периода колебаний напряжения в цепи).
Это легко получается, если приравнять обе формулы для мощности и решить получившееся тригонометрическое уравнение.

Если надо показать, как оно решается, то напишите

Определить полное ускорение а в момент времени t=3c точки, находящейся на ободе колеса радиусом R=0,5м, вращающегося согласно уравнению фи=A*t+B*t^3, где А=2рад\с, B=0,2рад\с^3.

ну, если не ошибаюсь, то ускорение равно e * R, где е — угловое ускорение, равное второй производной от фи по времени:
е=фи два штриха=6*В*t=3,6
а = е*R=3,6*0,5 = 1,8 м/с в квадрате

вроде так, но пусть ВОСХОД перепроверит=))

Ну тут-то все верно, только не полное решение.
Найдено только так называемое тангенсальное ускорение, которое изменяет модуль вектора скорости, а надо найти еще нормальное ускорение (в простонародье центростремительное), которое меняет направление вектора скорости.
Продолжим:

Читайте также: При износе зеркала цилиндров

а/полное/=корень(а/тангенсальное/^2 + a/нормальное/^2)
а/нормальное/=V^2/R, где V=w*R, V — линейная скорость точки обода в момент времени, а w — угловая скорость колеса в момент времени (она равна первой производной от фи).
Первая производная от фи=A+3*B*t^2, а момент времени t=3 (c) она равна w=7,4 (рад/с).
Тогда скорость V=7,4*0,5=3,7 (м/с)
а/нормальное/=(3,7^2)/0,5=27,38 (м/с^2)
а/полное/=корень(1,8^2+27,38^2)=27,44 (м/с^2)

Видео:Электромагнетизм Пр3.4. Теорема Гаусса. Поле бесконечного цилиндра.Скачать

Два бесконечно длинных коаксиальных цилиндра с радиусам

Продаж: 6 последняя 12.12.2020
Возвратов: 0

Загружен: 20.06.2017
Содержимое: 31621.PNG 30,74 Кбайт

Видео:ЧК_МИФ_ФМЛ_30 _ 3_1_4_7 (L2) ПОЛЕ РАВНОМЕРНО ЗАРЯЖЕННОГО ЦИЛИНДРАСкачать

Продавец

Видео:Теорема Гаусса - доказательство.Скачать

Описание товара

Два бесконечно длинных коаксиальных цилиндра с радиусами R1 = 10 мм и R2 = 20 мм заряжены: на внутреннем цилиндре поверхностная плотность зарядов равна 3,33 нКл/м^2, на внешнем 6,67 нКл/м^2. Найти разность потенциалов между цилиндрами.

Видео:43. Применение теоремы ГауссаСкачать

Дополнительная информация

Задача 31621. Подробное решение с краткой записью условия, формул и законов, используемых в решении, выводом расчетной формулы и ответом.
Если возникнут вопросы по решению, пишите. Постараюсь помочь.

Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Отзывы

Видео:ЭЛЕКТРОСТАТИКА.Задачи на применение теоремы Гаусса. 2022-2Скачать

С товаром «Два бесконечно длинных коаксиальных цилиндра с радиусам» также смотрят:

В целях противодействия нарушению авторских прав и права собственности, а также исключения необоснованных обвинений в адрес администрации сайта о пособничестве такому нарушению, администрация торговой площадки Plati (http://www.plati.market) обращается к Вам с просьбой — в случае обнаружения нарушений на торговой площадке Plati, незамедлительно информировать нас по адресу support@plati.market о факте такого нарушения и предоставить нам достоверную информацию, подтверждающую Ваши авторские права или права собственности. В письме обязательно укажите ваши контактные реквизиты (Ф.И.О., телефон).

В целях исключения необоснованных и заведомо ложных сообщений о фактах нарушения указанных прав, администрация будет отказывать в предоставлении услуг на торговой площадке Plati, только после получения от Вас письменных заявлений о нарушении с приложением копий документов, подтверждающих ваши авторские права или права собственности, по адресу: 123007, г. Москва, Малый Калужский пер. д.4, стр.3, Адвокатский кабинет «АКАР №380».

В целях оперативного реагирования на нарушения Ваших прав и необходимости блокировки действий недобросовестных продавцов, Plati просит Вас направить заверенную телеграмму, которая будет являться основанием для блокировки действий продавца, указанная телеграмма должна содержать указание: вида нарушенных прав, подтверждения ваших прав и ваши контактные данные (организиционно-правовую форму лица, Ф.И.О.). Блокировка будет снята по истечение 15 дней, в случае непредставления Вами в Адвокатский кабинет письменных документов подтверждающих ваши авторские права или права собственности.

Этот сайт использует cookie (куки) для обеспечения более эффективного пользовательского опыта. Подробнее читайте в нашей Политике использования файлов cookie.

Видео:Задача №2. Потенциал проводящей сферы.Скачать

Пожалуйста, внимательно ознакомьтесь с данной политикой использования файлов cookie, прежде чем пользоваться услугами plati.ru. Посещая сайт plati.ru вы соглашается с тем, что plati.ru может использовать файлы cookie для их последующей обработки системами Google Analytics, Яндекс.Метрика.

Что такое cookies?

Cookies — это простые текстовые файлы, которые хранятся на вашем компьютере или мобильном устройстве сервером веб-сайта. Каждый файл cookie уникален для вашего веб-браузера. Он содержит некоторую анонимную информацию, такую как уникальный идентификатор, доменное имя сайта, некоторые цифры и числа.

Необходимые файлы cookie позволяют нам предложить вам наилучший возможный опыт при доступе и навигации по нашему сайту и использовании его функций. Например, эти файлы cookie позволяют нам узнать, что вы создали учетную запись и вошли в нее.

Функциональные файлы cookie позволяют нам управлять сайтом в соответствии с вашим выбором. Например, мы узнаем ваше имя пользователя и запоминаем, как вы настраивали сайт при последующих посещениях.

Видео:Электрическое поле. Напряженность электрического поля. Силовые линии электрического поля. 10 класс.Скачать

Два бесконечно длинных коаксиальных цилиндра с радиусами 10

Работа поля. Напряженность. Потенциал

2101. Два электрона, находящиеся в начальный момент далеко друг от друга, движутся на встречу вдоль одной прямой с одинаковыми по модулю скоростями v _o = 1000 км/с. На какое наименьшее расстояние они сблизятся? решение

2102 . Два электрона находятся на большом расстоянии друг от друга. Вначале один электрон неподвижен, а другой приближается к нему с начальной скоростью v _o = 1000 км/с, направленной вдоль соединяющей электроны прямой. На какое наименьшее расстояние они сблизятся? С какими скоростями они разлетятся? решение

2103 . Четыре шарика, имеющие одинаковые заряды расположены вдоль одной прямой так, что расстояние между соседними шариками равно a. Какую работу A нужно совершить, чтобы разместить эти шарики: а) в вершинах квадрата со стороной a; б) в вершинах тетраэдра с ребром a? решение

2104 . Два одинаковых металлических шарика радиуса R = 1 мм соединены длинным тонким проводом. Один из них размещен в разреженном воздухе, а другой – посередине большой вакуумной камеры. На расположенный в вакууме шарик падает с большого расстояния поток электронов с начальной скоростью v _o = 3000 км/с. Какой заряд Q можно накопить таким способом на шариках? Каким будет ответ, если увеличить начальную скорость электронов до v _o / = 10000 км/с? Электрический пробой воздуха происходит при напряженности электрического поля E _o = 3 × 10 4 В/м. решение

2105 . По тонкому металлическому кольцу радиуса R равномерно распределен заряд q. определить напряженность поля E и потенциал j в точке A, расположенной на оси кольца на расстоянии h от его центра. решение

2106 . Электрон находится на оси тонкого кольца радиуса R на расстоянии h от его центра. Кольцо получает положительный заряд q и начинает притягивать электрон. Обязательно ли электрон пролетит через центр кольца? С какой скоростью v он может пролететь вблизи этой точки? решение

2107 . Чему равна напряженность электрического поля на поверхности проводника, если плотность поверхностного заряда s . решение

2108 . Внутри шара радиуса R имеется объемный заряд постоянной плотности r .

1) Найти зависимость напряженности электрического поля от расстояния до центра шара.

2) Найти зависимость потенциала от расстояния до центра шара. решение

2109 . Найти напряженность электрического поля внутри и вне бесконечно длинного цилиндра, заряженного объемной плотностью r . Радиус цилиндра R . решение

2110 . На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями s ₁ и s ₂. Требуется:

1) Используя теорему Остроградского-Гаусса: найти зависимость E(r) напряженности электрического поля от расстояния для трех областей I, II, III. Принять s ₁ = s , s ₂ = – s ;

2) Напряженность E в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора E, принять s = 30 нКл/м 2 , r = 4R;

Смотрите новый сайт В. Грабцевича по физике, а также шутки про школу.

Видео:Поле заряженной нитиСкачать

Два бесконечно длинных коаксиальных цилиндра с радиусами 10

Продемонстрируем возможности теоремы Остроградского-Гаусса на нескольких примерах.

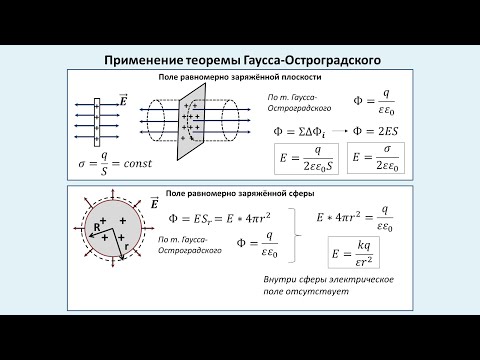
Поле бесконечной однородно заряженной плоскости

Поверхностная плотность заряда на произвольной плоскости площадью S определяется по формуле:

где d q – заряд, сосредоточенный на площади d S; d S – физически бесконечно малый участок поверхности.

Пусть σ во всех точках плоскости S одинакова. Заряд q – положительный. Напряженность во всех точках будет иметь направление, перпендикулярное плоскости S (рис. 2.11).

Очевидно, что в симметричных, относительно плоскости точках, напряженность будетодинакова по величине и противоположна по направлению.

Представим себе цилиндр с образующими, перпендикулярными плоскости, и основаниями ΔS, расположенными симметрично относительно плоскости (рис. 2.12).


Рис. 2.11	Рис. 2.12

Применим теорему Остроградского-Гаусса. Поток Ф_Е через боковую часть поверхности цилиндра равен нулю, т.к . Дляоснования цилиндра

Суммарный поток через замкнутую поверхность (цилиндр) будет равен:

Внутри поверхности заключен заряд . Следовательно, из теоремы Остроградского–Гаусса получим:

откуда видно, что напряженность поля плоскости S равна:

Полученный результат не зависит от длины цилиндра. Это значит, что на любом расстоянии от плоскости

Поле двух равномерно заряженных плоскостей

Пусть две бесконечные плоскости заряжены разноименными зарядами с одинаковой по величине плотностью σ (рис. 2.13).

Результирующее поле, как было сказано выше, находится как суперпозиция полей, создаваемых каждой из плоскостей .

Вне плоскостей напряженность поля

Полученный результат справедлив и для плоскостей конечных размеров, если расстояние между плоскостями гораздо меньше линейных размеров плоскостей (плоский конденсатор).

Между пластинами конденсатора действует сила взаимного притяжения (на единицу площади пластин):

Механические силы, действующие между заряженными телами, называют пондермоторными.

Тогда сила притяжения между пластинами конденсатора:

где S – площадь обкладок конденсатора. Т.к. , то

Это формула для расчета пондермоторной силы.

Поле заряженного бесконечно длинного цилиндра (нити)

Пусть поле создается бесконечной цилиндрической поверхностью радиуса R, заряженной с постоянной линейной плотностью , где d q – заряд, сосредоточенный на отрезке цилиндра (рис. 2.14).

Из соображения симметрии следует, что Е в любой точке будет направлена вдоль радиуса, перпендикулярно оси цилиндра.

Представим вокруг цилиндра (нити) коаксиальную замкнутую поверхность (цилиндр в цилиндре) радиуса r и длиной l (основания цилиндров перпендикулярно оси). Для оснований цилиндров для боковой поверхности т.е. зависит от расстояния r.

Следовательно, поток вектора через рассматриваемую поверхность, равен

При на поверхности будет заряд По теореме Остроградского-Гаусса , отсюда

Если , т.к. внутри замкнутой поверхности зарядов нет (рис.2.15).

Если уменьшать радиус цилиндра R (при ), то можно вблизи поверхности получить поле с очень большой напряженностью и, при , получить нить.

Поле двух коаксиальных цилиндров с одинаковой линейной плотностью λ, но разным знаком

Внутри меньшего и вне большего цилиндров поле будет отсутствовать (рис. 2.16) .

В зазоре между цилиндрами, поле определяется так же, как и в предыдущем случае:

Это справедливо и для бесконечно длинного цилиндра, и для цилиндров конечной длины, если зазор между цилиндрами намного меньше длины цилиндров (цилиндрический конденсатор).

Поле заряженного пустотелого шара

Пустотелый шар (или сфера) радиуса R заряжен положительным зарядом с поверхностной плотностью σ. Поле в данном случае будет центрально симметричным, – в любой точке проходит через центр шара. ,и силовые линии перпендикулярны поверхности в любой точке. Вообразим вокруг шара – сферу радиуса r (рис. 2.17).

Если то внутрь воображаемой сферы попадет весь заряд q, распределенный по сфере, тогда

Внутри сферы, при поле будет равно нулю, т.к. там нет зарядов: