- Урок по математике на тему : «Цилиндр и конус. Осевые сечения и сечения, параллельные основанию».
- Два сечения цилиндра параллельные основаниям
- Осевое сечение цилиндра прямого и наклонного. Формулы для площади сечения и его диагоналей
- Геометрическая фигура
- Прямой и наклонный цилиндры
- Осевое сечение прямого цилиндра
- Осевое сечение наклонного цилиндра
- Задача с прямым цилиндром
- Два сечения цилиндра параллельные основаниям
- 💡 Видео
Видео:№525. Площадь осевого сечения цилиндра равна 10 м2, а площадь основания — 5 м2.Скачать

Урок по математике на тему : «Цилиндр и конус. Осевые сечения и сечения, параллельные основанию».
Ищем педагогов в команду «Инфоурок»
Урок на тему « Цилиндр и конус. Осевые сечения и сечения, параллельные основанию.»
Познакомить учащихся с сечением, рассмотреть виды сечений цилиндра и конуса. Усеченный конус.
Сформировать у учащихся умения и навыки построения сечений
Применять полученные знания при решении задач.
Развивать: образное мышление, память, речь.
Воспитывать: интерес к предмету, самостоятельность, аккуратность.
Оборудование: Интерактивна доска, презентация на тему » Цилиндр и конус. Осевые сечения и сечения, параллельные основанию.»
Тип урока: Практическая работа
Организационный момент (2-3 мин)
Актуализация знаний. Повторение: (фронтальный опрос 5мин)
Объяснение нового материала: ввести понятие сечения, рассмотреть виды сечения (презентация 15 минут) ( приложение1 )
Работа в тетради построение сечений: Решение задач. (проверка знаний 15 мин) ( приложение2 )
1. Организационный момент. Приветствие учащихся.
2. Повторение: проверка усвоения материала
Объясните что такое круговой цилиндр (образующая цилиндра, основания и боковая поверхность цилиндра)
Какой цилиндр называется прямым?
Что такое радиус цилиндра
Что такое высота цилиндра
Что такое ось цилиндра.
Какая фигура называется конусом?
Что такое образующая конуса? Что можно сказать о них?
Что такое высота конуса?
Какой конус называется прямым?
Что такое ось конуса?
При помощи вращения какой фигуры можно получить конус?
Из чего состоит поверхность конуса?
3. Объяснение нового материала:
1. Рассмотреть виды сечения цилиндра (Слайд 3-6)
2. Рассмотреть касательную плоскости цилиндра (Слайд 7)
3.Рассмотреть конические сечения (Слайд 8-10)
4. Усеченный цилиндр. Обозначить его элементы (Слайд 11)
— Сложить руки в замок, обхватить ими затылок, направить локти вперёд. Подтянуть голову к локтям, не сопротивляясь, растягивать шейный отдел позвоночника. Тянуть 10-15 секунд.
— Растереть ладонями уши – сначала только мочки, а затем всё ухо целиком, вверх-вниз, взад-вперёд.
— При решении устных упражнений встать, потянуться наверх, если ответ верный, или наклониться вниз, если ответ неверный.
Нарисовать глазами стереометрические фигуры (пирамиду, призму, конус, цилиндр).
5. Закрепление изученного материала:
Задача№1. Осевое сечение конуса – прямоугольный треугольник. Найти площадь этого сечения, если радиус основания конуса равен 5 см.
Рис. 6. Иллюстрация к задаче
Дано: 

Найти:
Так как в осевом сечении всегда лежит равнобедренный треугольник, то 


Медиана SO в прямоугольном треугольнике, опущенная из прямого угла, равна половине гипотенузы:
Так как треугольник равнобедренный, то медиана равна высоте, следовательно:
Площадь треугольника равна:
Ответ:
Задача №2. Высота конуса равна 8, а длина образующей — 10. Найдите площадь осевого сечения этого конуса.
Читайте также: Цилиндр для накладного замка зн1 м1
Решение. Пусть образующая это L, высота это H, радиус основания это R.
Найдём диаметр основания и используя формулу площади треугольника вычислим площадь. По теореме Пифагора:
Вычисляем площадь сечения:
6. Итог урока: Назовите виды сечений конуса и цилиндра. Выставление оценок.
7. Домашнее задание: Решить задачи.
Найдите площадь сечения, если радиус цилиндра равен 2см, а высота цилиндра равна 3см.
В цилиндре проведено сечение через две образующие. Высота цилиндра Н, радиус r . Сечение отсекает от направляющей дугу в 60 0 . Найдите площадь сечения.
Видео:ЕГЭ Задание 14 Сечение цилиндраСкачать
Два сечения цилиндра параллельные основаниям
@ Цилиндрической поверхностью называется поверхность, образованная вращением прямой, параллельной оси вращения.
Прямым круговым цилиндром называется тело, ограниченное цилиндрической поверхностью и двумя плоскостями, перпендикулярными оси цилиндра. В дальнейшем такое тело будем называть просто цилиндром .
Часть поверхности между этими плоскостями называется боковой поверхностью цилиндра, круги, полученные в секущих плоскостях – основаниями цилиндра, часть образующей между основаниями называется образующей цилиндра .
Сечение, проходящее через ось цилиндра – осевое сечение , есть прямоугольник со сторонами, равными высоте цилиндра и диаметру основания.
Сечение, параллельное оси цилиндра – прямоугольник, стороны которого равны высоте цилиндра и хорде основания, не проходящей через центр.
Сечение, не перпендикулярное оси цилиндра, пересекающее боковую поверхность и не пересекающее основания цилиндра, представляет часть плоскости, ограниченную эллипсом.
Если боковую поверхность цилиндра разрезать вдоль образующей и развернуть, то получится прямоугольник, называемый разверткой боковой поверхности цилиндра, стороны которого равны высоте цилиндра и длине окружности основания.
Основные параметры, связанные с цилиндром: радиус основания (R), высота (Н), образующая (L), площадь основания ( ), площадь осевого сечения ( ), площадь боковой поверхности ( ), площадь полной поверхности ( ), объем цилиндра (V).
Любые пары перечисленных параметров кроме пар: высота и образующая, радиус основания и площадь основания, площадь осевого сечения и площадь боковой поверхности задают цилиндр, т.е. определяют его однозначно.
К формулам, связывающим эти понятия, относятся
Полезно по паре заданных параметров с помощью приведенных формул находить остальные.
Ответ: 1. , 2 p RH , 2 p (R + H) , .
Многие задачи, связанные с телами вращения, очевидным образом и сразу сводятся к задачам планиметрии.
Осевое сечение цилиндра – квадрат, площадь которого равна Q . Найти площадь основания. Решение Так как сторона данного квадрата равна диаметру основания, то . Тогда S осн .
Площадь осевого сечения цилиндра равна Q . Найти площадь боковой поверхности. Решение
Из определения осевого сечения следует, что его стороны равны Н и 2R . Тогда Q = 2 RH , S бок = 2 p RH = p Q .
Боковая поверхность и объем цилиндра выражаются одним числом. Определить диаметр цилиндра. Решение
Видео:Задача, которую боятсяСкачать

Осевое сечение цилиндра прямого и наклонного. Формулы для площади сечения и его диагоналей
Цилиндр — это симметричная пространственная фигура, свойства которой рассматривают в старших классах школы в курсе стереометрии. Для его описания используют такие линейные характеристики, как высота и радиус основания. В данной статье рассмотрим вопросы касательно того, что такое осевое сечение цилиндра, и как рассчитать его параметры через основные линейные характеристики фигуры.
Видео:№531. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельнойСкачать

Геометрическая фигура
Сначала дадим определение фигуре, о которой пойдет речь в статье. Цилиндр представляет собой поверхность, образованную параллельным перемещением отрезка фиксированной длины вдоль некоторой кривой. Главным условием этого перемещения является то, что отрезок плоскости кривой принадлежать не должен.
На рисунке ниже показан цилиндр, кривая (направляющая) которого является эллипсом.
Здесь отрезок длиной h является его образующей и высотой.
Видно, что цилиндр состоит из двух одинаковых оснований (эллипсы в данном случае), которые лежат в параллельных плоскостях, и боковой поверхности. Последней принадлежат все точки образующих линий.
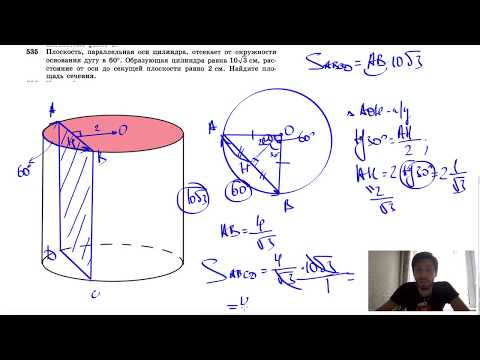
Видео:№535. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 60Скачать
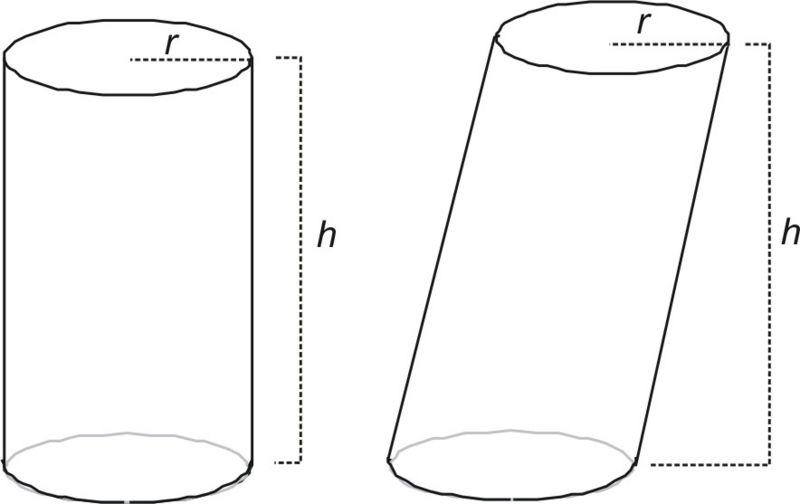
Прямой и наклонный цилиндры
Перед тем как переходить к рассмотрению осевого сечения цилиндров, расскажем, какие типы этих фигур бывают.
Если образующая линия перпендикулярна основаниям фигуры, тогда говорят о прямом цилиндре. В противном случае цилиндр будет наклонным. Если соединить центральные точки двух оснований, то полученная прямая называется осью фигуры. Приведенный рисунок демонстрирует разницу между прямым и наклонным цилиндрами.
Видно, что для прямой фигуры длина образующего отрезка совпадает со значением высоты h. Для наклонного цилиндра высота, то есть расстояние между основаниями, всегда меньше длины образующей линии.
Далее охарактеризуем осевые сечения обоих типов цилиндров. При этом будем рассматривать фигуры, основаниями которых является круг.
Видео:№523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высотуСкачать

Осевое сечение прямого цилиндра
Осевым называется любое сечение цилиндра, которое содержит его ось. Это определение означает, что осевое сечение будет всегда параллельно образующей линии.
В цилиндре прямом ось проходит через центр круга и перпендикулярна его плоскости. Это означает, что рассматриваемое сечение круг будет пересекать по его диаметру. На рисунке показана половинка цилиндра, которая получилась в результате пересечения фигуры плоскостью, проходящей через ось.
Не сложно понять, что осевое сечение прямого круглого цилиндра представляет собой прямоугольник. Его сторонами являются диаметр d основания и высота h фигуры.
Запишем формулы для площади осевого сечения цилиндра и длины hd его диагонали:
Прямоугольник имеет две диагонали, но обе они равны друг другу. Если известен радиус основания, то не сложно переписать эти формулы через него, учитывая, что он в два раза меньше диаметра.
Видео:🔴 Радиус основания цилиндра равен 15, а его ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

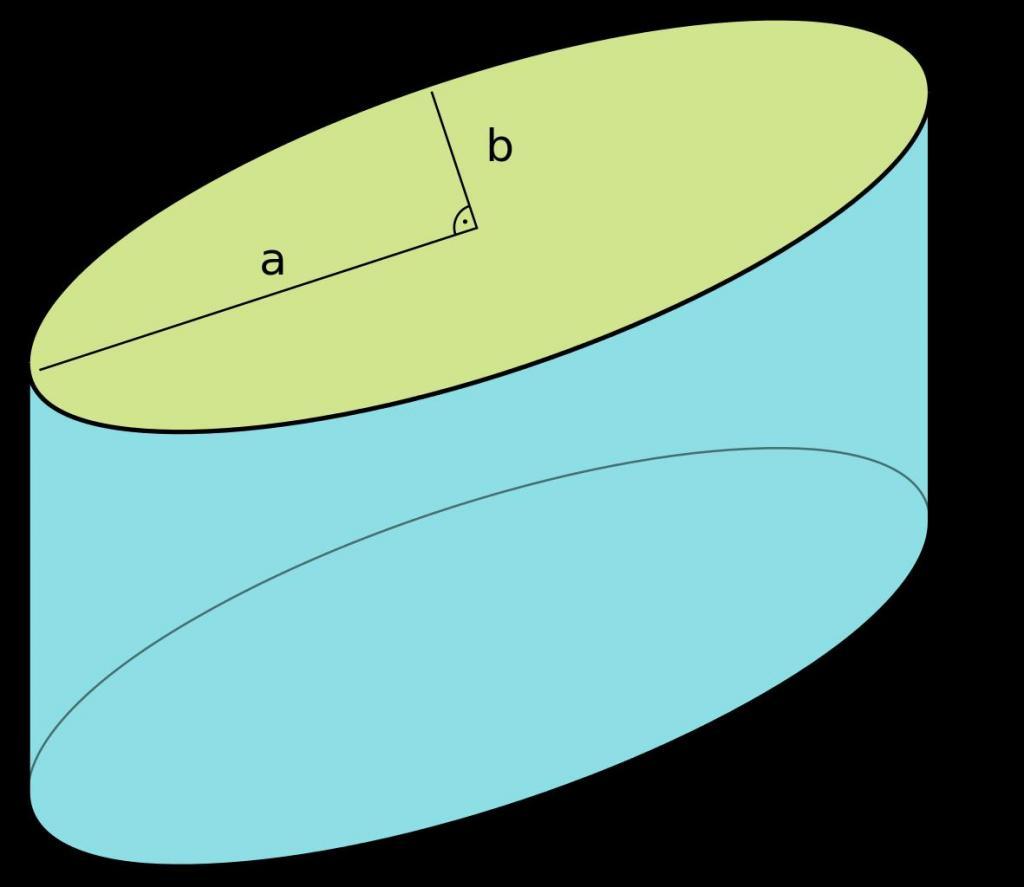
Осевое сечение наклонного цилиндра
Рисунок выше демонстрирует наклонный цилиндр, изготовленный из бумаги. Если выполнить его осевое сечение, то получится уже не прямоугольник, а параллелограмм. Его стороны — это известные величины. Одна из них, как и в случае сечения прямого цилиндра, равна диаметру d основания, другая же — длина образующего отрезка. Обозначим ее b.
Для однозначного определения параметров параллелограмма недостаточно знать его длины сторон. Необходим еще угол между ними. Предположим, что острый угол между направляющей и основанием равен α. Он же и будет углом между сторонами параллелограмма. Тогда формулу для площади осевого сечения наклонного цилиндра можно записать следующим образом:
Диагонали осевого сечения цилиндра наклонного рассчитать несколько сложнее. Параллелограмм имеет две диагонали разной длины. Приведем без вывода выражения, позволяющие рассчитывать диагонали параллелограмма по известным сторонам и острому углу между ними:
Здесь l1 и l2 — длины малой и большой диагоналей соответственно. Эти формулы можно получить самостоятельно, если рассмотреть каждую диагональ как вектор, введя прямоугольную систему координат на плоскости.
Видео:Видеоурок по математике "Цилиндр"Скачать

Задача с прямым цилиндром
Покажем, как использовать полученные знания для решения следующей задачи. Пусть дан круглый прямой цилиндр. Известно, что осевое сечение цилиндра — квадрат. Чему равна площадь этого сечения, если площадь поверхности всей фигуры составляет 100 см2?
Для вычисления искомой площади необходимо найти либо радиус, либо диаметр основания цилиндра. Для этого воспользуемся формулой для общей площади Sf фигуры:
Поскольку сечение осевое представляет собой квадрат, то это означает, что радиус r основания в два раза меньше высоты h. Учитывая это, можно переписать равенство выше в виде:
Теперь можно выразить радиус r, имеем:
Поскольку сторона квадратного сечения равна диаметру основания фигуры, то для вычисления его площади S будет справедлива следующая формула:
Мы видим, что искомая площадь однозначно определяется площадью поверхности цилиндра. Подставляя данные в равенство, приходим к ответу: S = 21,23 см2.
Видео:№521. Докажите, что осевое сечение цилиндра является прямоугольником, две противоположныеСкачать

Два сечения цилиндра параллельные основаниям
Высота цилиндра равна 3, а радиус основания равен 13.
а) Постройте сечение цилиндра плоскостью, проходящей параллельно оси цилиндра, так, чтобы площадь этого сечения равнялась 72.
б) Найдите расстояние от плоскости сечения до центра основания цилиндра.
а) Пусть OO1 — ось цилиндра. Проведем AB и CD параллельно оси цилиндра. Проведем BD и AC. Так как через две параллельные прямые проходит единственная плоскость, то прямоугольник BDCA — искомое сечение (см. рис.).
б) В этом прямоугольнике одна сторона будет равняться высоте цилиндра, а вторая — хорде окружности, лежащей в основании. Так как то где x — хорда AC. Проведем OH перпендикулярно AC. В силу того, что треугольник ACO равнобедренный, точка H также будет являться серединой AC. Тогда из прямоугольного треугольника, у которого гипотенуза — радиус OC, а один катет — половина этой хорды, находим второй катет OH по теореме Пифагора.
Таким образом, расстояние от центра окружности до сечения равно 5.
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
💡 Видео
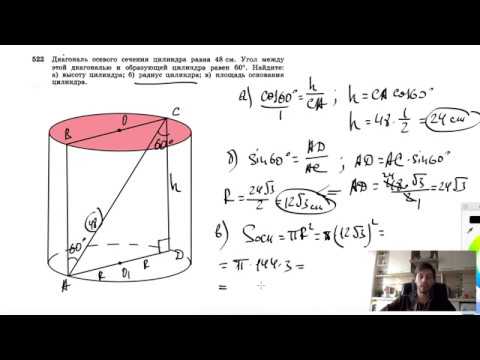
№522. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующейСкачать
Объём цилиндраСкачать

Тема 4. Цилиндр. Осевое сечение цилиндра. Развертка боковой поверхности цилиндра. Площадь боковойСкачать

2 задание ЕГЭ профиль стереометрияСкачать

11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

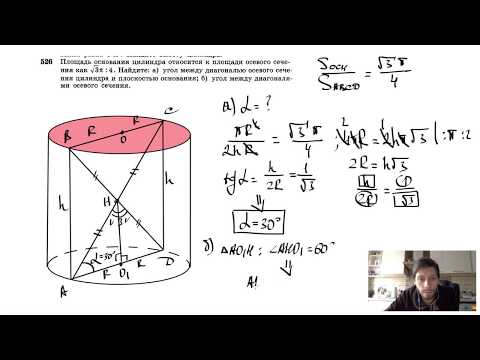
№526. Площадь основания цилиндра относится к площади осевого сечения как √3π:4. Найдите:Скачать
2 задание ЕГЭ профиль стереометрияСкачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

ЕГЭ. Математика. База . Задача 16.Площадь осевого сечения цилиндраСкачать

11 класс, 27 урок, Сечения цилиндрической поверхностиСкачать

№529. Высота цилиндра равна 8 см, радиус равен 5 см. Найдите площадь сечения цилиндраСкачать