Два цилиндра под прямым углом

На рис. 197 приведен случай пересечения двух цилиндров под прямым углом. Горизонтальные проекции линий пересечения совпадают с контуром вертикально расположенного цилиндра. Пересечение фронтальных проекций крайних образующих линий цилиндров определяет точки 1₂, 2₂, 3₂ и 4₂ С помощью горизонтальных проекций 5₁ и 6₁ находят фронтальные проекции 5₂ и 6₂ передних точек линий пересечения. Для нахождения промежуточных точек проводят горизонтальную плоскость ?. Эта плоскость пересечет вертикальный цилиндр по окружности, горизонтальная проекция которой совпадает с контуром этого цилиндра. Горизонтально расположенный цилиндр пересечется с плоскостью ? по образующим, которые удобнее найти с помощью третьей проекции (точки 73, 83). При отсутствии третьей проекции пользуются вспомогательной полуокружностью плоскости П₂. Она позволяет определить расстояние у от образующих до оси цилиндра. Получив горизонтальную проекцию 7₁ находят ее фронтальную проекцию 7₂ на фронтальной проекции ?₂ плоскости-посредника ?. Задачу решают путем проведения ряда таких плоскостей.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284966965_two-cylinders.jpg|—>TEnd—>

Линию пересечения в изометрической проекции строят с помощью одного из оснований цилиндров, в данном случае с помощью левого основания горизонтального цилиндра. От соответствующих точек этого основания по образующим откладывают величины, взятые с фронтальной или горизонтальной проекций цилиндра. Таким путем на чертеже построены точки 7′, 5′ и обведена четвертая часть передней (левой) линии пересечения; другие точки линии пересечения находятся аналогично; задняя (правая) линия пересечения в этом примере будет невидимой.

Видео:Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Пересечение двух цилиндров

Пересечение двух цилиндров является одной из основных задач начертательной геометрии, выполнение которой требует знания основ создания проекций.

Рассмотрим пример пересечения двух цилиндров под прямым углом из курса начертательной геометрии. Они параллельны профильной плоскости проекции (подразумевается, что оси вращения не пересекаются, а смещены друг от друга на некоторую величину а).

Ось малого цилиндра является перпендикулярной к горизонтальной плоскости проекции. Фронтальная проекция пересечения совпадает с очертанием большего цилиндра на отрезке между точками 1 и 7.

Таким образом, задача сводится к нахождению точек линии пересечения на проекции (профильной).

1. Для этого удобно применить вспомогательные секущие плоскости уровня. Для их равномерного расположения, проекцию основания вертикального цилиндра делят на 12 частей.
2. Затем через точки деления проводятся образующие, после чего выявляются точки их пересечений с поверхностью горизонтального цилиндра (фронтальная проекция).
3. Профильные линии точек находятся по линиям связи.
4. Для начала построения аксонометрии пересекающихся цилиндров необходимо изобразить их очерки (рисунок б).
5. Для нахождения опорных точек на горизонтальном цилиндре можно построить контур нормального сечения вокруг точки В.
6. Для нахождения точек, которые принадлежат линии перехода, необходимо рассечь цилиндры вспомогательными плоскостями уровня. Они пересекут оба цилиндра по образующим.
7. В пересечениях соответствующих образующих находятся промежуточные (рис. в-д) и характерные точки (1,4,7,10) линии перехода, которую ищем.
8. Найденные точки соединяются плавной кривой.
9. Готовый изометрический вид пересечения двух цилиндров изображен на рисунке е.

Читайте также: Замок управление от цилиндра

Видео:Задача, которую боятсяСкачать

Тело пересечения цилиндров

Видео:Как построить ЛИНИЮ ПЕРЕСЕЧЕНИЯ двух ЦИЛИНДРОВСкачать

Взаимное пересечение поверхностей

Видео:СОЕДИНЕНИЕ ЦИЛИНДРОВ В BLENDER/РАЗНЫЕ СПОСОБЫСкачать

6. ОСОБЫЕ СЛУЧАИ ПЕРЕСЕЧЕНИЯ. ТЕОРЕМА МОНЖА

1. Поверхности в точках касания имеют общие касательные плоскости.

Теорема (о двойном соприкосновении)

Если две поверхности второго порядка имеют две точки соприкосновения и общие касательные плоскости в этих точках, то линия их пересечения распадается на две плоские кривые второго порядка.

Сфера и эллиптический цилиндр пересекаются по двум окружностям. Они имеют две общие точки А и В и две общие касательные плоскости в этих точках. Пространственная линия пересечения распалась на две плоские кривые — окружности (рисунок 128).

2. Две пересекающиеся поверхности касаются третьей поверхности второго порядка.

Теорема (теорема Г.Монжа)

Если две пересекающиеся поверхности второго порядка могут быть описаны вокруг третьей поверхности второго порядка или вписаны в нее, то они пересекаются по двум плоским кривым второго порядка.

Теорема Монжа — частный случай теоремы о двойном соприкосновении. Например, поверхности конуса и цилиндра с общей фронтальной плоскостью симметрии касаются сферы по окружностям 1″—2″ и 3″—4″. Линия пересечения поверхностей представляет собой два эллипса, плоскости которых перпендикулярны фронтальной плоскости проекций (рисунок 129).

На рисунок 130 даны два конуса, описанные вокруг одного и того же шара. Оси которых пересекаются под прямым углом. Построить линию пересечения заданных поверхностей.

Наивысшие 1, 3 и наинизшие 2, 4 точки линии перехода находят в пересечении крайних образующих на фронтальной проекции заданных поверхностей. Если сфера касается обеих поверхностей, то линия их пересечения распадается на две плоские кривые (в нашем примере — на два различных эллипса). На фронтальной проекции эти эллипсы изображаются отрезками прямых, а на горизонтальной — эллипсами.

Точки 5 и 6 пересечения эллипсов находят на окружности радиуса c» / 2. Построение промежуточных точек ясно из чертежа.

Для определения видимости линий пересечения на горизонтальной проекции проводят секущую плоскость Р (через ось конуса с вершиной S ). Точки 7, 8 и 9, 10 служат границами раздела между видимой и невидимой частями линий пересечения. На фронтальной проекции невидимая часть линии пересечения сливается с видимой.

На рисунок 131 даны два цилиндра с одинаковыми диаметрами. Оси цилиндров пересекаются под прямым углом.

Здесь в пересечении цилиндров получаются два одинаковых эллипса 1—2 и 3—4, которые проецируются на плоскость V в виде прямых, а на плоскость Н — в виде окружностей, сливающихся с проекцией основания одного из цилиндров.

Видео:Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Кратчайшие линии на поверхности цилиндра

Рубрика: Технические науки

Дата публикации: 09.04.2016 2016-04-09

Статья просмотрена: 477 раз

Библиографическое описание:

Эгамов, Н. М. Кратчайшие линии на поверхности цилиндра / Н. М. Эгамов. — Текст : непосредственный // Молодой ученый. — 2016. — № 8 (112). — С. 361-363. — URL: https://moluch.ru/archive/112/28358/ (дата обращения: 31.10.2021).

Известно, что поверхность цилиндра имеет систему прямых линий, параллельных оси цилиндра, а следовательно, и друг другу. Эти прямые называются образующими цилиндра.

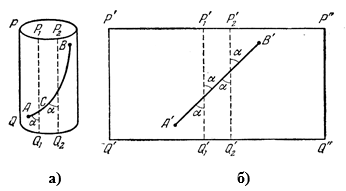
Зададим на поверхности цилиндра две точки Аи В (рис.1-а). Будем искать среди кривых, расположенных на цилиндре и соединяющих точки Аи В, ту, которая обладает наименьшей длиной. Обозначим эту кратчайшую кривую, соединяющую точки Аи В, через АВ. Сначала рассмотрим случай, когда Аи В не лежат на одной образующей.

Читайте также: Цилиндр найти площадь поверхности цилиндра если объем равен

Разрежем боковую поверхность цилиндра по некоторой образующей РQ (не пересекающей АВ) и развернем ее на плоскость; получим некоторый прямоугольник (рис.1-б) (одна пара сторон прямоугольника, Р′Р″ и Q″Q″, получилась от развертывания окружностей, ограничивающих боковую поверхность цилиндра; друга пара P′Q′ и P″Q″, образовалась из двух краев разреза РQ). Образующие цилиндра перейдут в прямые, параллельные стороне Р′Q′ прямоугольника. Точки Аи В перейдут в точки А′и B′ лежащей внутри прямоугольника. Линии, соединяющие на цилиндре точки Аи В, перейдут в плоские линии, соединяющие точки А′ и B′ внутри прямоугольника. Дуга АВ — кратчайшая из линий на цилиндре, соединяющих точки Аи В — перейдет в кратчайшую из плоских линий, соединяющих точки А′ и B′ т. е. в прямолинейный отрезок А′ B′. Таким образом, после развертывания боковой поверхности цилиндра в плоский прямоугольник кратчайшая дуга АВ на поверхности цилиндра переходит в прямолинейный отрезок А′B′. Образующие цилиндра Р₁Q₁, Р₂Q₂ … переходит в прямые Р₁′Q₁′, Р₂′Q₂′ …, параллельные сторонам Р′Q′, Р″Q″ прямоугольника Р′Q′, Q″Р″. Углы, которые образует отрезок А′B′ с этими прямыми, равны как соответственные углы при параллельных линиях. Обозначим величину каждого из них через α.

Теперь свернем прямоугольник Р′Q′, Q″Р″ (склеив его противоположные стороны Р′Q′ и Р″ Q″) так, чтобы он вновь принял первоначальную форму цилиндра. Точки А′ и В′ перейдут вновь в точки А и В цилиндра, а прямолинейный отрезок А′В′, их соединяющий- в кратчайшую дугу АВ на поверхности цилиндра; углы отрезка А’В’ с прямыми Р₁′Q₁′, Р₂′Q₂′ перейдут в равные им углы между дугой АВ и образующими Р₁′Q₁′, Р₂″ Q₂″ …цилиндра. Так как прямая А’В’ пересекла все прямые, параллельные Р′Q′, под равными углами α, то кратчайшая дуга АВ в которую переходит А′В′, пересекает все образующие цилиндра под равными углами α (рис.1-а).

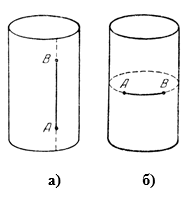
Рассмотрим особый случай, когда точки Аи В лежат на одной образующей (рис.2-а). В этом случае, очевидно, отрезок АВ образующей будет кратчайшим расстоянием между точками А и В на поверхности цилиндра.

Выделим еще случай, когда точки Аи В лежат на одном круговом сечении цилиндра (рис.2-б). Дуга АВ этого сечения перпендикулярна ко всем образующим. Она служим кратчайшей дугой, соединяющей точки А и В.

Если разрезать цилиндр по образующей, не пересекающей дуги АВ, и развернуть его в плоский прямоугольник, то в двух особо рассмотренных случаях кратчайшая дуга перейдет в отрезок, параллельный сторонам прямоугольника. Во всех остальных случаях кратчайшая линия пересекает образующие под углом, отличным от прямого (и не равным нулю).

Винтовой линией называется линия на поверхности цилиндра, которая пересекает все образующие цилиндра под равными углами, отличными от прямого.

Будем обозначать угол между винтовой линией и образующие через α. Линия, пересекающая образующие цилиндра под прямым углом, есть круговое сечение. Можно рассматривать круговое сечение как предельный случай винтовой линии, когда α обращается в прямой угол. Точно так же образующую цилиндра можно рассматривать как другой предельный случай, когда α обращается в нуль.

Читайте также: Шайбы под ваз цилиндры

Рассмотрим два движения по поверхности цилиндра: движение параллельное оси (по образующей), и вращение вокруг оси (по круговому сечению) с постоянными скоростями.

Каждое из этих движений можно вести в двух противоположных направлениях. Будем считать на вертикальном цилиндре движение вверх положительным вращением вращение на вертикальном цилиндре справа налево (для того, кто стоит вдоль оси головой вверх), или против движения часовой стрелки. Будем считать отрицательным вращением вращение слева направо — движению часовой стрелки.

Движение по винтовой линии получается в результате складывания двух движений: движения, параллельного оси цилиндра, и вращения вокруг оси. Винтовая линия называется правой, если по ней движение вверх сочетается с положительным вращением — справа налево (рис. 3), левой, если по ней движение вверх сопровождается отрицательным вращением (слева направо).

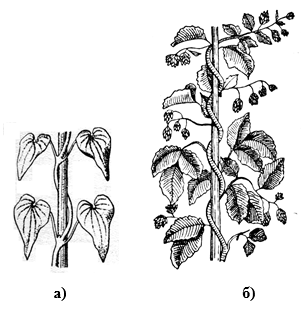
Большинство вьющихся растений (вьюнок, фасоль), завиваясь вокруг вертикальной опоры, принимает форму правых винтовых линий (рис.4-а). С другой стороны, хмель, например, принимает форму левой винтовой линии (рис.-4б).

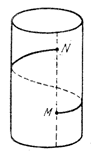
Пусть, двигаясь по винтовой линии, точка пересечет некоторую образующую в точке М, а при продолжении движения по винтовой линии она вновь пересечет эту же образующую в точке N; когда точка прошла дугу MN винтовой линий, она совершила полный оборот вокруг оси цилиндра; в это же время она прошла вверх расстояние, равное длине отрезка MN (рис.3). Если скорость вращательного движения равно нулю, и точка перемещается только параллельно оси цилиндра по образующей, наступает первый предельный случай; другой предельный случай наступит, если скорость перемещения, параллельного оси цилиндра, равна нулю и точка только вращается вокруг оси по окружности.

Видео:Сложная 2-я задача Профиля #егэ #математика #геометрия #стереометрия #цилиндр #шар #репетиторСкачать

Калькулятор развертки усеченного плоскостью цилиндра онлайн

Видео:ТЕМА 3. ПРИНЦИПЫ ПЕРЕСЕЧЕНИЯ ЦИЛИНДРА И ШАРА С ПРЯМЫМИ ПЛОСКОСТЯМИСкачать

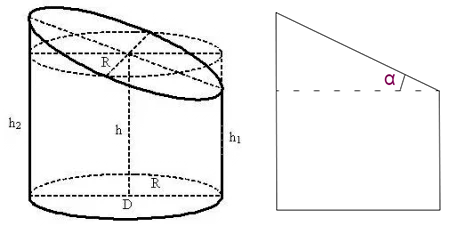
Обозначения

• R — радиус основания цилиндра;
• D — диаметр основания цилиндра;
• h — средняя высота усечённого цилиндра;
• h1 — наименьшая высота усечённого цилиндра;
• h2 — наибольшая высота усечённого цилиндра;
• α — угол сечения, град.
• X_{1 .. n} — координаты для построения развёртки по оси X;
• Y_{1 .. n} — координаты для построения развёртки по оси Y;

Числовые значения в таблице заполняются числом (5; 5.16; -3.12), либо математическим выражением (5/7; (1-5)*2.13)

Введите радиус или диаметр *:

Введите высоты * и (или) угол:

Без макс. и мин. высоты можно посчитать только площади боковой поверхности и основания и объём

Или введите одну из высот и угол сечения (рис.)

Округление:

Построение развёртки:

Видео:ОБЪЕМ ЦИЛИНДРА #shorts #егэ #огэ #математика #профильныйегэСкачать

Графики

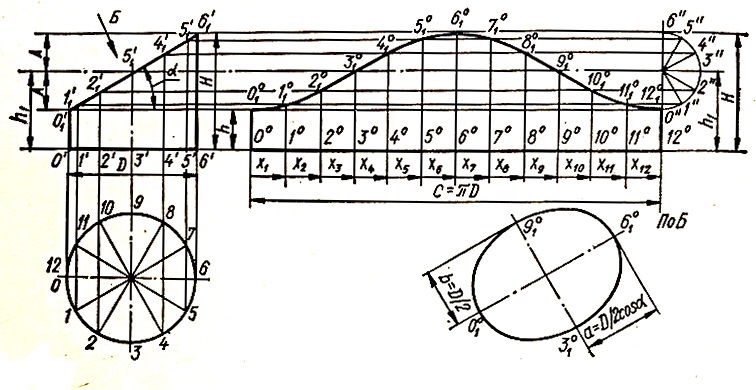
Чертится развертка усеченного плоскостью цилиндра, как показано на рисунке:

Видео:Пересечение двух цилиндров. Инженерная графикаСкачать

Формулы

Формула для вычисления значений Y:

Y_i = D * tg(α) * sin (i * (180 / n)) , здесь: i — номер точки, α — угол сечения, n — количество точек развертки, D — диаметр цилиндра;

Формула для вычисления значений X:

X_i = ((π * R 2 ) / n) * i , здесь: i — номер точки, α — угол сечения, n — количество точек развертки, R — радиус цилиндра, π — число Пи (прим. 3.14);

🎦 Видео

Гениальная доработка дрели, которая позволит сверлить строго вертикально / DIY drill upgradeСкачать

День студента мехмата МГУ #мгу #умскул #физика #математика #учеба #подготовкаогэ #подготовкакегэСкачать

усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать

Центр кругаСкачать

ТРИ ПРИЗНАКА РАВЕНСТВА ТРЕУГОЛЬНИКОВ НА ЕГЭ #shorts #математика #егэ #огэ #профильныйегэ #геометрияСкачать

ЗАБУДЬ О КРИВЫХ ОТВЕРСТИЯХ ТЕПЕРЬ ТОЧНО ПРОСВЕРЛИШЬ ЛЮБОЙ ДРЕЛЬЮСкачать

Как отрезать и соединить трубу под любым углом без расчётов и спец инструмента.Скачать

Сперматозоид-чемпион | наглядно показано оплодотворениеСкачать

СТРОГО ПО ЦЕНТРУ !!! БЕЗ СТАНКА И ТОКАРЯ, как просверлить отверстие в болтеСкачать

Студенты российского вуза разработали вечный двигатель #вечныйдвигатель #изобретенияСкачать

Геометрия. Цилиндр. Задача 2Скачать