Два цилиндра в изометрии

Видео:Как начертить цилиндр в объемеСкачать

Урок 8. Построение линии пересечения поверхностей цилиндров

Здравствуйте! На сегодняшнем уроке мы построим линию пересечения поверхностей двух цилиндров.

Исходное задание берем из задачника С. К. Боголюбова, 1989 год, стр. 141, вар. 1.

При выполнении задания воспользуемся безосным способом проецирования, т. е. без обозначения осей координат.

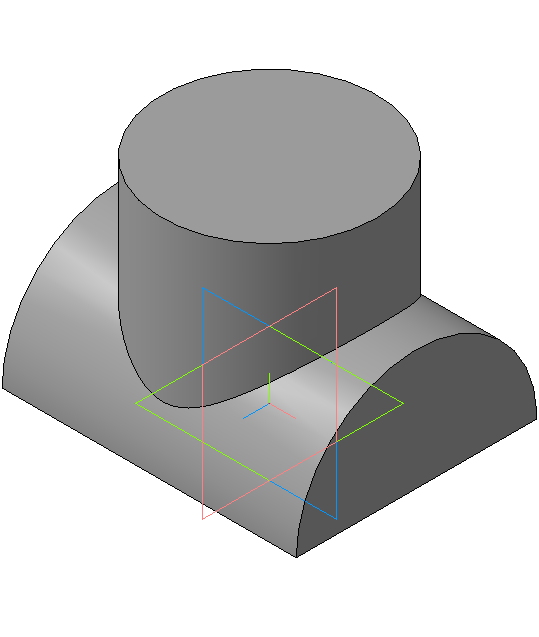
Я предлагаю вам сначала сделать 3d модель пересекающихся цилиндров, а затем, на ассоциативном чертеже построить линию пересечения цилиндров.

Видео:Как построить ЛИНИЮ ПЕРЕСЕЧЕНИЯ двух ЦИЛИНДРОВСкачать

Создание ассоциативного чертежа пересекающихся цилиндров

1. Сначала на плоскости zx (горизонтальной) вычерчиваем окружность диаметром 80 мм, выдавливаем на 80 мм.

2. Затем на плоскости zy создаем эскиз полуцилиндра радиусом 45 мм.

Выдавливаем эскиз на длину 110 мм, направление выдавливания – средняя плоскость .

3. Создаем чертеж, вставляем стандартные виды и изометрию детали. Щелкнув правой кнопкой мыши по габаритному прямоугольнику, разрушаем связи проекций с моделью. Это нам нужно для того, чтобы перестроить линии пересечения вручную.

4. Удаляем линии пересечения на фронтальной проекции и изометрии. Конечно, можно все оставить и так, Компас построил линию пересечения цилиндров очень точно. Но так как нам нужно показать свои знания, мы перестроим линию вручную.

Как построить линию пересечения цилиндров?

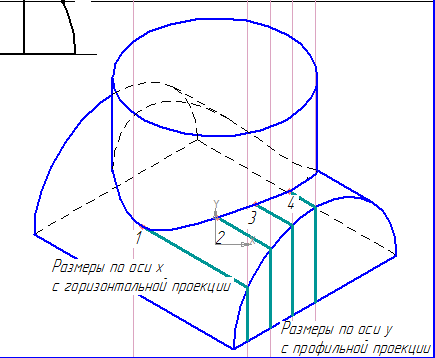
Построение линии пересечения двух цилиндров начинаем с нахождения проекций очевидной точки 4 и характерной точки 1. Делаем это по линиям связи.

Затем на профильной проекции проводим две вспомогательные секущие плоскости Pw и Pw1 произвольно.

Далее находим проекции точек пересечения плоскостей с контуром детали, по линиям связи.

При помощи кривой Безье соединяем полученные точки на фронтальной проекции.

На изометрии точки находятся путем перенесения соответствующих координат точек по осям x и y и соединения их кривой Безье.

Координаты точки 1 находим, проведя вспомогательную прямую через середину нижнего основания модели.

Готовый чертеж с вновь построенной линией пересечения поверхностей цилиндров.

Возможно, вас заинтересует урок по моделированию корпуса водопроводного крана, в нем также реализовано построение линии пересечения поверхностей вращения.

Пример подробно разобран в видеоуроке. Посмотрите его.

Итак, сегодня вы научились строить линию пересечения двух цилиндров на ортогональных проекциях и в изометрии.

Видео:Построение изометрии цилиндраСкачать

Изометрическая проекция (окончание)

Видео:2 2 3 построение изометрии окружностиСкачать

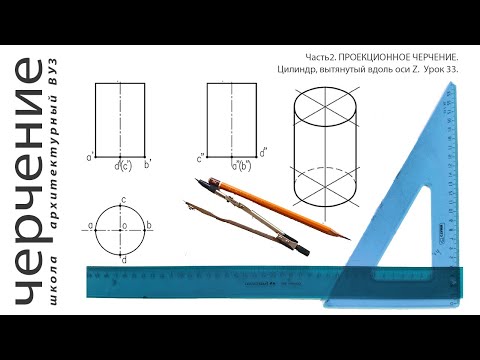
Изометрия окружности

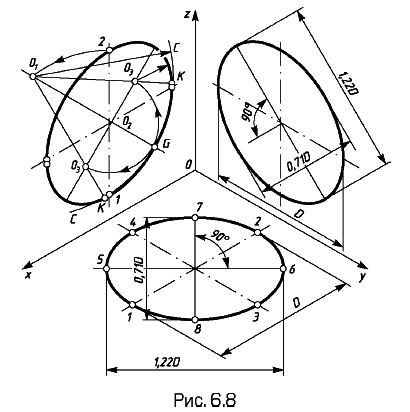
Окружности в изометрии изображаются в виде эллипсов (рис. 6.8) с указанием величин осей эллипсов для приведенных коэффициентов искажения, равных единице.

Большая ось эллипсов расположена под углом 90° для эллипсов, лежащих в плоскости xOz к оси у, в плоскости yOz к оси х, в плоскости xOy к оси z.

При построении изометрического изображения от руки (как рисунка) эллипс выполняют по восьми точкам. Например, по точкам 1, 2, 3, 4, 5, 6, 7 и 8 (см. рис. 6.8). Точки 1, 2, 3 и 4 находят на соответствующих аксонометрических осях, а точки 5, 6, 7 и 8 строят по величинам соответствующих большой и малой осей элипса. При вычерчивании эллипсы в изометрической проекции можно заменять овалами и строить их следующим образом 1 . Построение показано на рис. 6.8 на примере эллипса, лежащего в плоскости xOz. Из точки 1 как из центра, делают засечку радиусом R = D на продолжении малой оси эллипса в точке О₁ (строят также аналогичным образом и симметричную ей точку, которая на чертеже не показана). Из точки O₁ как из центра проводят дугу CGC радиуса D, которая является одной из дуг, составляющих контур эллипса. Из точки О₂ как из центра проводят дугу радиуса O₂G до пересечения с большой осью эллипса в точках О₃. Проводя через точки О₁, O₃ прямую, находят в пересечении с дугой CGCточку K, которая определяет O₃K — величину радиуса замыкающей дуги овала. Точки K являются также точками сопряжения дуг, составляющих овал.

Видео:2 2 1 изометрия по чертежуСкачать

Изометрия цилиндра

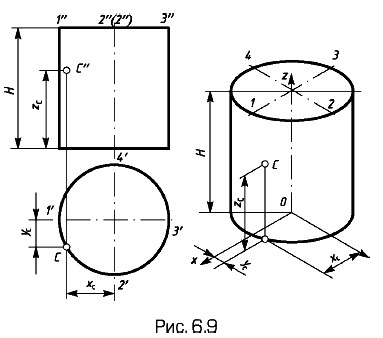
Изометрическое изображение цилиндра определяется изометрическими изображениями окружностей его основания. Построение в изометрии цилиндра высотой Н по ортогональному чертежу (рис. 6.9, слева) и точки С на его боковой поверхности показано на рис. 6.9, справа.

Пример построения в изометрической проекции круглого фланца с четырьмя цилиндрическими отверстиями и одним треугольным приведен на рис. 6.10. При построении осей цилиндрических отверстий, а также ребер треугольного отверстия использованы их координаты, например координаты х₀ и y₀.

Видео:Цилиндр, вытянутый вдоль оси Z. Урок33.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Два цилиндра в изометрии

Видео:Изометрическая проекция цилиндра. Чертим вместе.Скачать

§ 13. Построение аксонометрических проекций

Построение аксонометрических проекций начинают с проведения аксонометрических осей.

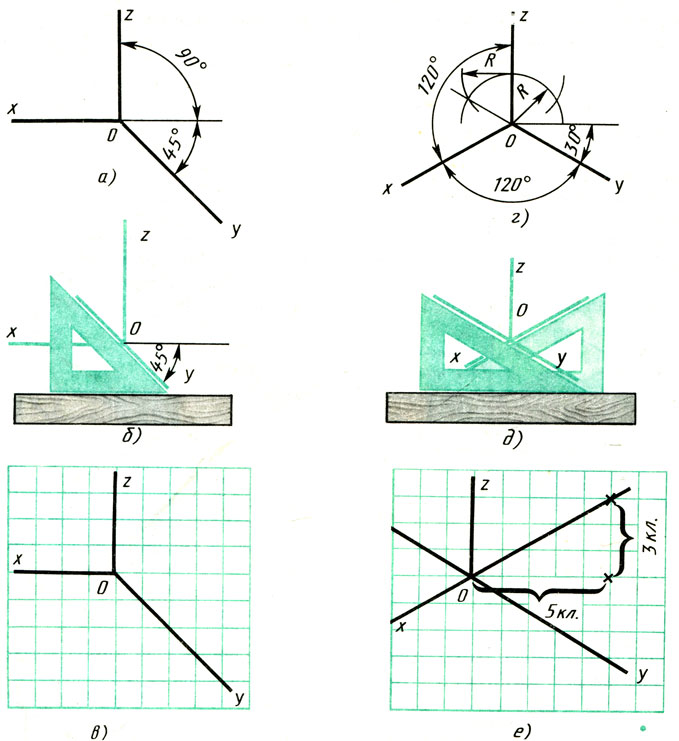
Положение осей. Оси фронтальной ди-метрической проекции располагают, как показано на рис. 85, а: ось х — горизонтально, ось z — вертикально, ось у — под углом 45° к горизонтальной линии.

Угол 45° можно построить при помощи чертежного угольника с углами 45, 45 и 90°, как показано на рис. 85, б.

Положение осей изометрической проекции показано на рис. 85, г. Оси х и у располагают под углом 30° к горизонтальной линии (угол 120° между осями). Построение осей удобно проводить при помощи угольника с углами 30, 60 и 90° (рис. 85, д).

Чтобы построить оси изометрической проекции с помощью циркуля, надо провести ось z, описать из точки О дугу произвольного радиуса; не меняя раствора циркуля, из точки пересечения дуги и оси z сделать засечки на дуге, соединить полученные точки с точкой О.

При построении фронтальной диметрической проекции по осям х и z (и параллельно им) откладывают действительные размеры; по оси у (и параллельно ей) размеры сокращают в 2 раза, отсюда и название «диметрия», что по-гречески означает «двойное измерение».

При построении изометрической проекции по осям х, у, z и параллельно им откладывают действительные размеры предмета, отсюда и название «изометрия», что по-гречески означает «равные измерения».

На рис. 85, в и е показано построение аксонометрических осей на бумаге, разлинованной в клетку. В этом случае, чтобы получить угол 45°, проводят диагонали в квадратных клетках (рис. 85, в). Наклон оси в 30° (рис. 85, г) получается при соотношении длин отрезков 3 : 5 (3 и 5 клеток).

Рис. 85. Способы построения осей аксонометрических проекций

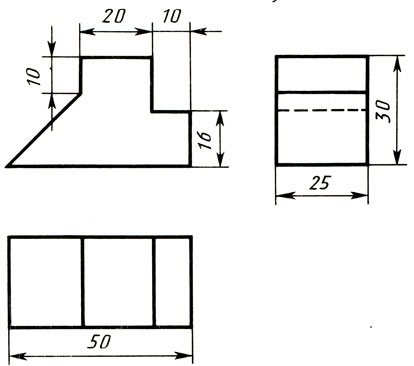
Построение фронтальной диметрической и изометрической проекций. Построить фронтальную диметрическую и изометрическую проекции детали, три вида которой приведены на рис. 86.

Рис. 86. Комплексный чертеж детали

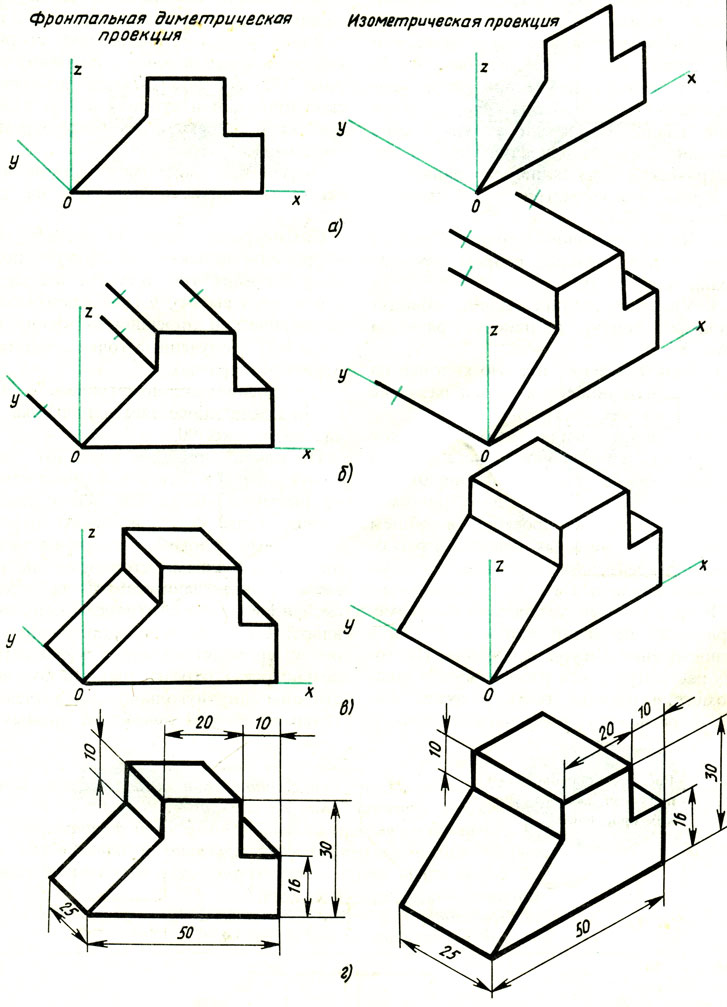
Порядок построения проекций следующий (рис. 87):

1. Проводят оси. Строят переднюю грань детали, откладывая действительные величины высоты — вдоль оси z, длины — вдоль оси х (рис. 87, а).

2. Из вершин полученной фигуры параллельно оси v проводят ребра, уходящие вдаль. Вдоль них откладывают толщину детали: для фронтальной ди-метрической проекции — сокращенную в 2 раза; для изометрии — действительную (рис. 87, б).

3. Через полученные точки проводят прямые, параллельные ребрам передней грани (рис. 87, в).

4. Удаляют лишние линии, обводят видимый контур и наносят размеры (рис. 87, г).

Сравните левую и правую колонки на рис. 87. Что общего и в чем различие данных на них построений?

Рис. 87. Способ построения аксонометрических проекций

Из сопоставления этих рисунков и приведенного к ним текста можно сделать вывод о том, что порядок построения фронтальной диметрической и изометрической проекций в общем одинаков. Разница заключается в расположении осей и длине отрезков, откладываемых вдоль оси у.

В ряде случаев построение аксонометрических проекций удобнее начинать с построения фигуры основания. Поэтому рассмотрим, как изображают в аксонометрии плоские геометрические фигуры, расположенные горизонтально.

Построение аксонометрической проекции квадрата показано на рис. 88, а и б.

Вдоль оси х откладывают сторону квадрата а, вдоль оси у — половину стороны а/2 для фронтальной диметрической проекции и сторону а для изометрической проекции. Концы отрезков соединяют прямыми.

Рис. 88. Аксонометрические проекции квадрата: а — фронтальная диметрическая; б — изометрическая

Построение аксонометрической проекции треугольника показано на рис. 89, а и б.

Симметрично точке О (началу осей координат) по оси х откладывают половину стороны треугольника а/2, а по оси у — его высоту h (для фронтальной диметрической проекции половину высоты h/2). Полученные точки соединяют отрезками прямых.

Рис. 89. Аксонометрические проекции треугольника: а — фронтальная диметрическая; б — изометрическая

Построение аксонометрической проекции правильного шестиугольника показано на рис. 90.

По оси х вправо и влево от точки О откладывают отрезки, равные стороне шестиугольника. По оси у симметрично точке О откладывают отрезки s/2, равные половине расстояния между противоположными сторонами шестиугольника (для фронтальной диметрической проекции эти отрезки уменьшают вдвое). От точек m и n, полученных на оси у, проводят вправо и влево параллельно оси х отрезки, равные половине стороны шестиугольника. Полученные точки соединяют отрезками прямых.

Рис. 90. Аксонометрические проекции правильного шестиугольника: а — фронтальная диметрическая; б — изометрическая

Ответьте на вопросы

1. Как располагают оси фронтальной диметрической и изометрической проекций? Как их строят?

Читайте также: Бмв нет искры во всех цилиндрах

2. Какие размеры откладывают вдоль осей фронтальной диметрической и изометрической проекций и параллельно им?

3. Вдоль какой аксонометрической оси откладывают размер уходящих вдоль ребер предмета?

4. Назовите общие для фронтальной диметрической и изометрической проекций этапы построения.

Задания к § 13

Упражнение 40

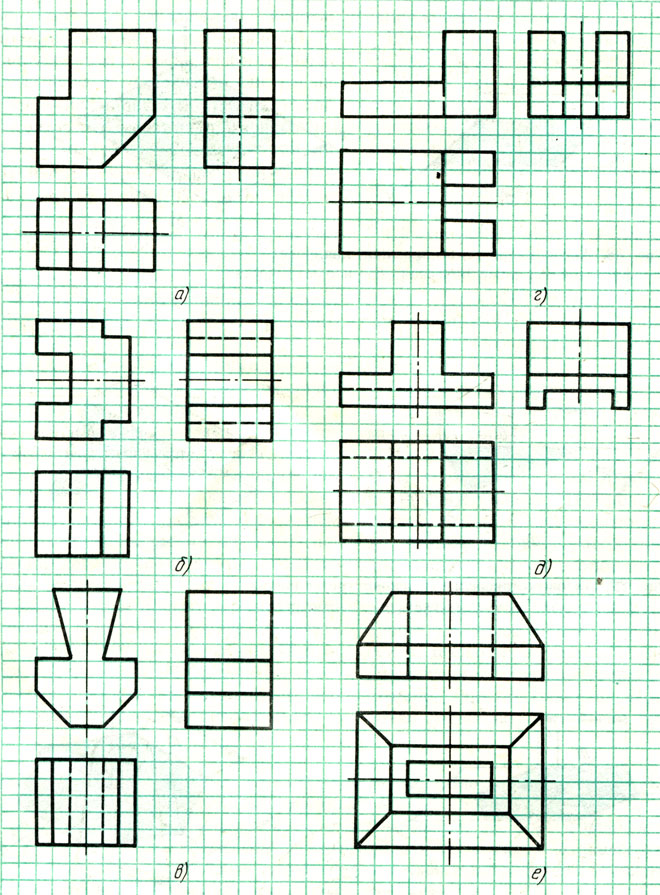
Постройте аксонометрические проекции деталей, приведенных на рис. 91, а, б, в — фронтальные диметрические, для деталей на рис. 91, г, д, е — изометрические.

Размеры определите по числу клеток, считая, что сторона клетки равна 5 мм.

В ответах дано по одному примеру последовательности выполнения заданий.

Рис. 91. За типе на построение аксонометрических проекций

Упражнение 41

Постройте в изометрической проекции правильные четырехугольную, треугольную и шестиугольную призмы. Основания призм расположены горизонтально, длина сторон основания 30 мм, высота 70 мм.

В ответах дан пример последовательности выполнения задания.

Видео:Задание 50. Построение ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ЦИЛИНДРОВСкачать

Взаимное пересечение поверхностей тел с примерами и образцами выполнения

Взаимное пересечение поверхностей. Поверхности могут взаимно пересекаться. При этом линии одной поверхности пересекаются с другой поверхностью и образуют точки, которые в совокупности представляют линию пересечения.

Видео:Цилиндр, вытянутый вдоль оси X. Урок 35.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

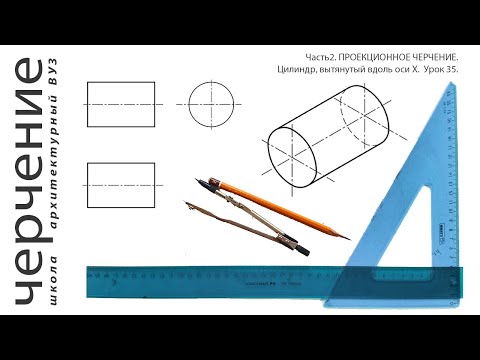
Пересечение прямой линии с поверхностями тел

Конструкции деталей можно рассматривать как сочетание различных геометрических тел. Необхо­димо уметь строить линии пересечения поверхнос­тей этих тел. Пример, где требуется подобное по­строение, показан на рис. 195, на котором изо­бражен бункер, ограниченный цилиндрической поверхностью А, пересекающейся с конической поверхностью Б и поверхностью пирамиды В.

В зависимости от вида поверхностей тел линии пересечения могут быть лекальными кривыми или ломаными.

Для решения задач на построение линий пере­сечения поверхностей необходимо предварительно усвоить построение точек пересечения прямой с поверхностями различных геометрических тел.

Если прямая пересекается с поверхностью тела, получаются две точки, одновременно принадлежа­щие как поверхности тела, так и прямой линии. Такие точки называются точками входа и выхода (рис. 196. а; точки N и М). Для нахождения этих точек выполняются построения в следующем по­рядке.

Через данную прямую проводят вспомогатель­ную плоскость (обычно проецирующую). Напри­мер, на рис. 196, а, где изображено пересечение прямой АВ с поверхностью пирамиды, через пря­мую проведена вспомогательная горизонтально-проецирующая плоскость Р. Затем находят линии пересечения вспомогательной плоскости с повер­хностью данного геометрического тела (линии КС и ЕD). На пересечении полученных линий с за­данной прямом находят искомые точки (точки N и М).

На комплексном чертеже точки входа и выхода определяют следующим образом (рис. 196. б). Горизонтальные проекции kс и ed прямых КС и ED совпадают с горизонтальным следом плоскости Р_H. Фронтальные проекции точек k‘, с’, е’ и d‘ определяют, пользуясь вертикальными линиями связи, проведенными из точек k, с, е и d до пере­сечения с фронтальными проекциями основания пирамиды. Соединяют точки k‘ с с’ и е’ с d‘ прямыми. На пересечении фронтальных проекций найденных прямых с проекцией а’Ь’ данной пря­мой получают фронтальные проекции n‘ и т’ искомых точек входа и выхода. Проведя через них вертикальные линии связи, находят горизонталь­ные проекции п и т этих точек.

В некоторых частных случаях можно обой­тись без применения вспомогательной плоскос­ти. Например, точки входа и выхода прямой АВ с поверхностью прямого кругового цилин­дра (рис. 197, а) определяют следующим образом.

Горизонтальная проекция цилиндрической по­верхности представляет собой окружность, поэто­му горизонтальные проекции всех точек, располо­женных на цилиндрической поверхности, в том числе и двух искомых точек, будут расположены на этой окружности (рис. 197, а).

Фронтальные проекции n‘ и m‘ искомых точек определяют, проводя через точки n и m верти­кальные линии связи до встречи с данной фрон­тальной проекцией а’Ь’ прямой АВ.

На рис. 197, б, в показано построение точек входа и выхода прямой АВ и поверхности прямого кругового конуса. Через прямую АВ проводят вспомогательную плоскость Р, проходящую через вершину конуса. Плоскость Р пересечет конус по образующим SH₃ SH_4.

На комплексном чертеже изображение плос­кости Р строят следующим образом. На прямой АВ берут произвольную точку К и соединяют ее с вершиной S конуса прямой линией. Две пересе­кающиеся прямые АВ и SK определяют плоскость Р.

Чтобы найти точки входа и выхода, необходимо построить горизонтальные проекции образующих SH₃ и SH₄. Для этого продолжим s’k’ и а’b‘ до пересечения с осью х в точках h‘₂ и h‘₁. Опустим линию связи из точки k‘ до пересечения с ab, полученную точку k соединим с s. Продлим гори­зонтальную проекцию прямой SK до пересечения с линией связи, опушенной из точки h‘₂, получим точку h₂. Из точки h‘₁ проведем линию связи до пересечения с продолжением прямой ab, получим точку h₁. Через следы h₁ и h₂ пройдет горизон­тальный след плоскости Р. Точки h₁ и h₂ соеди­ним прямой и получим горизонтальный след Р_Н плоскости Р.

Основание конуса является горизонтальным следом конической поверхности. Поэтому, опреде­лив точки пересечения этого следа со следом Р_Н плоскости Р, можно найти и те две образующие, по которым коническая поверхность пересекается вспомогательной плоскостью Р. На комплексном чертеже горизонтальная проекция основания ко­нуса (окружность) пересекается со следом Р_Н в точках h₃ и h₄. Эти точки соединяют с вершиной s и получают следы sh₃ и sh₄ образующих SH₃ и SH₄.

На пересечении найденных образующих с дан­ной прямой АВ находят искомые точки М и N — точки входа и выхода прямой АВ с конической поверхностью.

Горизонтальные проекции точек т и n находят на пересечении горизонтальных проекций обра­зующих sh₃ и sh₄ с горизонтальной проекцией прямой ab. Через точки m и n проводят вертикальные линии связи до пересечения а’b‘ и нахо­дят фронтальные проекции т‘ и n‘ точек входа и выхода.

Точки входа и выхода прямой АВ с повер­хностью сферы (рис. 198) находят, проведя через прямую АВ вспомогательную фронтально-проецирующую плоскость Р.

Вспомогательная плоскость Р пересекает сферу по окружности, которая проецируется на плос­кость Н в виде эллипса, что затрудняет построе­ние. Поэтому в данном случае необходимо приме­нить способ перемены плоскостей проекций. Но­вую плоскость проекций выбирают так, чтобы вспомогательная плоскость Р была бы ей парал­лельна, т.с. следует провести новую ось проекций x₁ так. чтобы она была параллельна фронтальной проекции а’b‘ прямой АВ (для упрощения по­строении на рис. 198 ось x₁ проведена через про­екцию а’b‘).

Затем необходимо построить новую горизон­тальную проекцию a₁b₁ прямой АВ и новую го­ризонтальную проекцию окружности диаметра D, по которой плоскость Р пересекает сферу. На пересечении новых горизонтальных проекций двух искомых точек m_> и n_> Обратным построе­нием определяем фронтальные т’ и n‘ и горизон­тальные т и п проекции точек входа и выхода.

Видео:Усеченный цилиндр: проекции сечения, изометрия, развертка поверхностиСкачать

Линии пересечения и перехода

Многие детали машин представляют собой кон­струкции из пересекающихся геометрических тел. Общая линия пересекающихся поверхностей на­зывается линией пересечения.

На чертежах линии пересечения поверхностей изображаются сплошной основной линией (рис. 199, а). В местах перехода поверхностей литых и штампованных деталей нет четкой линии пересечения. Воображаемая линия пересечения называется линией перехода и условно изобража­ется на чертежах сплошной тонкой линией. Эта линия начинается и заканчивается в точках пере­сечения продолжения контура взаимно пересека­ющихся поверхностей (рис. 199. б).

Встречаются детали, имеющие всевозможные линии пересечения и перехода поверхностей. Особенно много линий перехода у поверхностей дета­лей, изготовленных литьем.

На рис. 200, а на приборе для испытания твер­дости видны линии переходов различных повер­хностей.

Кожух и крышка смесительного аппарата (рис. 200. б) имеют разнообразные линии перехо­да. Здесь можно видеть линии взаимного пересе­чения цилиндрических и других поверхностей.

Построение линий пересечения и перехода поверхностей при выполнении чертежей трубопрово­дов, вентиляционных устройств, резервуаров, кожухов машин, станков требует точности.

Видео:усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать

Общие правила построения линий пересечения поверхностей

Метод построения линий пересечения повер­хностей тел заключается в проведении вспомога­тельных секущих плоскостей и нахождении от­дельных точек линий пересечения данных повер­хностей в этих плоскостях.

Построение линии пересечения поверхностей тел начинают с нахождения очевидных точек. Например, на рис. 201, где изображены линии пересечения призмы с конусом, такими точками являются точки А и В. Затем определяют харак­терные точки, расположенные, например, на очерковых образующих поверхностей вращения или крайних ребрах, отделяющих видимую часть линий перехода от невидимой. На рис. 201 это точки С и D. Они располагаются на крайних ребрах верхней горизонтальной грани призмы.

Все остальные точки линии пересечения назы­ваются промежуточными (например, точки Е и F). Обычно их определяют с помощью вспомога­тельных параллельных секущих плоскостей (рис. 201, а).

В качестве вспомогательных плоскостей выби­рают такие плоскости, которые пересекают обе заданные поверхности по простым линиям — пря­мым или окружностям, причем окружности до­лжны располагаться в плоскостях, параллельных плоскостям проекций.

В данном примере плоскость Р рассекает конус по окружности (рис. 201, в), с помощью которой находят горизонтальные проекции точек е и f.

Во всех случаях. перед тем как строить линию пересечения поверхностей на чертеже, необходи­мо представить себе эту линию в пространстве (рис. 201, б).

Видео:Задание 38. Как начертить ИЗОМЕТРИЮ усеченного цилиндраСкачать

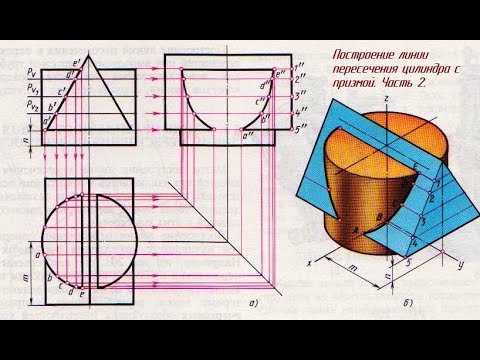
Пересечение поверхностей цилиндра и призмы

На рис. 202 показано построение проекции линий пересечения поверхности треугольной при­змы с поверхностью прямого кругового цилиндра. Боковые грани призмы перпендикулярны плоскос­ти V (рис. 202, а), поэтому фронтальная проекция линий пересечения поверхностей этих тел совпа­дает с фронтальной проекцией основания призмы. Горизонтальные проекции линий пересечения поверхностей совпадают с горизонтальной проек­цией цилиндра и являются окружностью. Про­фильные проекции точек А и Е находим по гори­зонтальным и фронтальным проекциям с по­мощью линий связи. Для построения проекций промежуточных точек В, С, D используем вспомо­гательные секущие плоскости Р_V, Р_V1 и Р_V2, c помощью которых находим фронтальные проек­ции b‘, с’. d‘ точек B, С. D.

В данном примере можно обойтись без вспомо­гательных секущих плоскостей, намечая произво­льно на фронтальной проекции точки b‘, с’, d‘.

Опуская линии связи на горизонтальную проек­цию, находим горизонтальные проекции с, Ь, d точек С, В, D. На профильной проекции с помощью линий связи находим проекции Ь», с”, d«.

На рис. 202, б показано построение изометри­ческой проекции. После построения изометричес­кой проекции цилиндра, используя размеры т и п (рис. 202, а), строят изометрическую проекцию основания призмы, на котором находят точки 1, 2. 3. 4. 5. От этих точек откладывают расстояния 1«е». 2“d« и т.п., взятые с профильной проекции комплексного чертежа, и находят точки А, В. С, D. Е

На изометрической проекции линия пересече­ния поверхностей цилиндра и призмы получается соединением точек А, В. С, D, Е, которые строят­ся но координатам, взятым с комплексного чертежа.

Читайте также: Момент инерции полого толстостенного цилиндра

Видео:Задание 54. Аксонометрия ЛИНИИ ПЕРЕСЕЧЕНИЯ цилиндра и призмы трехгранной Часть 2Скачать

Пересечение цилиндрических поверхностей

При выполнении машиностроительных черте­жей наиболее часто встречается случай пересече­ния двух цилиндрических поверхностей, оси кото­рых расположены под углом 90 0 .

Разберем пример построения линии пересече­ния поверхностей двух прямых круговых цилин­дров. оси которых перпендикулярны к плоскостям проекций (рис. 203, а).

В начале построения, как известно, находим проекции очевидных точек 1, 7 и 4.

Построение проекций промежуточных точек показано на рис. 203, б. Если в данном примере применить общий способ построения линий пере­сечения с помощью вспомогательных взаимно параллельных плоскостей, пересекающих обе цилин­дрические поверхности по образующим, то на пересечении этих образующих будут найдены искомые промежуточные точки линии пересече­ния (например, точки 2, 3, 5 на рис. 203, а). Од­нако в данном случае выполнять такое построение нет необходимости по следующим соображениям.

Горизонтальная проекция искомой линии пере­сечения поверхностей совпадает с окружностью — горизонтальной проекцией большого цилиндра. Профильная проекция линии пересечения также совпадает с окружностью — профильной проекци­ей малого цилиндра. Таким образом, фронталь­ную проекцию искомой линии пересечения легко найти по общему правилу построения кривой линии по точкам, когда две проекции точек извес­тны. Например, по горизонтальной проекции точ­ки 3 (рис. 203, б) находят профильную проекцию 3″. Но двум проекциям 3 и 3″ определяют фрон­тальную проекцию 3′ точки 3. принадлежащей линии пересечения цилиндров.

Построение изометрической проекции пересека­ющихся цилиндров начинают с построения изометрической проекции вертикального цилин­дра. Далее через точку а₁ параллельно оси х про­водят ось горизонтального цилиндра. Положение точки О₁ определяется величиной h₁, взятой с комплексного чертежа (рис. 203, б). Отрезок, равный h, откладываем от точки О вверх по оси z (рис. 203, в). Откладывая от точки О₁ по оси горизонтального цилиндра отрезок l, получим точку О₂ — центр основания горизонтального цилиндра.

Изометрическая проекция линии пересечения поверхностей строится по точкам с помощью трех координат. Однако в данном примере искомые точки можно построить иначе.

Так, например, точки 3 и 2 строят следующим образом. От центра О₂ (рис. 203, в) вверх, парал­лельно оси z, откладывают отрезки т и п, взятые с комплексного чертежа. Через концы этих отрез­ков прямые, параллельные оси у, до пересечения с основанием горизонтального цилиндра в точках 3₁ и 2₁. Затем из точек 1. 3 проводят прямые, параллельные оси х, и на них откладывают отрез­ки, равные расстоянию от основания горизонтального цилиндра до линии пересечения, взятые с фронтальной или горизонтальной проекции комплексного чертежа. Конечные точки этих отрезков будут принадлежать линии пересечения. Через полученные точки проводят по лекалу кривую, выделяя се видимые и невидимые части.

Пример взаимного пересечения цилиндрических поверхностей с осями, перпендикулярными друг к другу, приведен на рис. 204, а. Одна цилиндрическая поверхность корпуса имеет вертикальную ось, а другая (половина цилиндра) — горизонталь­ную.

Если диаметры пересекающихся цилиндричес­ких поверхностей одинаковы. то профильная про­екция линии пересечения представляет собой две пересекающиеся прямые (рис. 204, б).

Если пересекающиеся цилиндрические поверхности имеют оси, расположенные под углом, отличным от прямого угла, то линию их пересечения строят с помощью вспомогательных секущих плоскостей или другими способами (например, способом сфер).

Видео:Построение прямоугольной изометрии детали (ДГР-5)Скачать

Пересечение поверхностей многогранников

При пересечении двух многогранников линия пересечения поверхностей представляет собой ломаную линию.

Если ребра двух призм взаимно перпендикуляр­ны (рис. 205, а), то линия пересечения призм строится следующим образом.

Горизонтальная и профильная проекции линии пересечения совпадают соответственно с горизон­тальной проекцией пятиугольника (основания одной призмы) и с профильной проекцией четырехугольника (основания другой призмы). Фрон­тальную проекцию ломаной линии пересечения строят по точкам пересечения ребер одной призмы с гранями другой.

Например, взяв горизонтальную 1 и про­фильную 1″ проекции точки 1 пересечения ребра пятиугольной призмы с гранью четырех­угольной (рис. 205, а) и пользуясь известным приемом построения, с помощью линии связи можно легко найти фронтальную проекцию 1′ точки 1, принадлежащей линии пересечения призм.

Изометрическая проекция двух пересекающих­ся призм (рис. 205, б) может быть построена по координатам соответствующих точек.

Например, изометрическую проекцию двух точек 5 и 5₁, симметрично расположенных на левой грани пятиугольной призмы, строят так. Принимая для удобства построений за начало координат точку О, лежащую на верхнем основа­нии пятиугольной призмы, откладываем влево от О по оси х отрезок ОЕ, величину которого берут с комплексного чертежа на фронтальной или горизонтальной проекции. Далее из точки Е вниз параллельно оси z откладываем отрезок EF, рав­ный а, и, наконец, от точки F влево и вправо параллельно оси у откладываем отрезки F5 и F5_1, равные с/2.

Далее от точки F параллельно оси х откладыва­ем отрезок n, взятый с комплексного чертежа. Через его конец проводим прямую, параллельную оси у, и откладываем на ней отрезок, равный с. Вниз параллельно оси z откладываем отрезок, равный Ь, и параллельно у — отрезок, равный k. В результате получаем изометрию основания че­тырехугольной призмы.

Точки 1 и 4 на ребрах пятиугольной призмы можно построить, используя только одну коорди­нату z.

Примеры, где требуются подобные построения, показаны на рис. 206, на которых видны линии пересечения поверхностей призм.

Линию пересечения поверхностей четыреху­гольной призмы с четырехугольной пирамидой (рис. 207, а) строят по точкам пересечения ребер одного многогранника с гранями другого многогранника.

Например, проекции точек 1 и 3 искомой ли­нии пересечения находят следующим образом. Фронтальные проекции 1‘ и 3′ очевидны. Про­фильные проекции 1“ и 3“ и горизонтальные 1 и 3 находят с помощью линий связи. Аналогично находят точки 2 и 4.

Линию пересечения поверхностей четыреху­гольной призмы с четырехугольной пирамидой (рис. 207, а) строят по точкам пересечения ребер одного многогранника с гранями другого многогранника.

Например, проекции точек 1 и 3 искомой ли­нии пересечения находят следующим образом. Фронтальные проекции 1‘ и 3′ очевидны. Про­фильные проекции 1“ и 3“ и горизонтальные 1 и 3 находят с помощью линий связи. Аналогично находят точки 2 и 4.

На рис. 207, б и в показана последовательность построения диметрической проекции. Сначала строят пирамиду. Для построения призмы от точ­ки О откладывают отрезок ОО₁, взятый с фрон­тальной проекции комплексного чертежа (О’ О’₁ ). и получают точку О₁ (рис. 207, б). Через точку О₁ проводят параллельно оси х ось симметрии призмы и по ней от точки откладывают вправо и влево половины высоты призмы. Через точки О₂ и О₃ проводят прямые, параллельные осям у и z, на которых откладывают соответственно половину и целую длину диагоналей четырехугольника основания призмы. Соединив концы диагоналей прямыми, получают диметрическую проекцию основания призмы.

Диметрические проекции точек пересечения 2. 4, б. 8 ребер призмы и пирамиды получаются без дополнительных построений (рис. 207, в).

Диметрические проекции точек пересечения 1, 3, 5. 7 ребер пирамиды с гранями призмы находят по координатам известным способом.

В этом примере диметрические проекции точек 1, 3, 5 и 7 можно построить иначе. От середины левого основания призмы — точки О₂ — отклады­ваем вверх и вниз по оси z соответственно отрезки т и n, взятые с комплексного чертежа. Через концы отрезков т и n проводят прямые, парал­лельные оси у, до пересечения с контуром основания призмы в точках А, В, С и D. Через эти точ­ки проводят прямые, параллельные оси х, до пе­ресечения с ребрами пирамиды. В результате по­лучают искомые точки 1, 3, 5 и 7.

На рис. 208 показан корпус оптического компа­ратора, который имеет элементы пересечения поверхностей пирамид и призм. На рисунке видна линия пересечения поверхностей этих тел.

Видео:Цилиндр, вытянутый вдоль оси Y. Урок 34.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Пересечение поверхностей цилиндра и конуса

Пример пересечения поверхностей цилиндра и конуса показан на рис. 209, б. Построение линии пересечения поверхностей прямого кругового усе­ченного конуса, имеющего вертикальную ось, с цилиндром, расположенным горизонтально, пока­зано на рис. 209, а. Оси цилиндра и конуса пере­секаются в точке О₁ и лежат в одной плоскости.

Как и ранее, сначала определяют проекции очевидных 1, 7 и характерных 4, 10 точек линии пересечения.

Для определения промежуточных точек прово­дят вспомогательные горизонтальные секущие плоскости Р₁…Р₅. (рис. 209, а). Они будут рассе­кать конус по окружности, а цилиндр по образую­щим (рис. 209, б). Искомые точки линии пересе­чения находятся на пересечении образующих с окружностями.

Читайте также: Замена рабочего цилиндра сцепления бмв е39

Для определения горизонтальных проекций точек пересечения из центра O₁ проводят горизонтальные проекции дуг окружностей (рис. 209, а), по которым вспомогательные плос­кости Р₁…Р₅ пересекают конус. Размеры радиусов этих дуг окружностей взяты с профильной про­екции.

Так как профильные проекции точек 1“… 12“ известны, то, проводя линии связи до пересечения с соответствующими дугами окружностей, находят горизонтальные проекции точек 1… 12. Используя линии связи, по двум имеющимся проекциям, профильной и горизонтальней, находим фронталь­ные проекции точек пересечения 1‘. 12’.

Полученные на фронтальной и горизонтальной проекциях точки, принадлежащие к линии пере­сечения. обводят по лекалу.

На горизонтальной проекции часть линии пере­сечения будет видимой, а часть — невидимой. Границу этих частей линии пересечения определяют с помощью вспомогательной секущей плос­кости Р₃, проведенной через ось цилиндра. Точки, расположенные над плоскостью Р₃ (см. профиль­ную проекцию), будут на плоскости Н видимы, а точки, расположенные под плоскостью Р_3,— неви­димы.

Изометрическую проекцию пересекающихся поверхностей цилиндра и конуса вычерчивают в такой последовательности. Вначале выполняют изометрическую проекцию конуса (рис. 209, в). Затем от центра О нижнего основания конуса по его оси вверх откладывают координату ОО₁ = h и получают точку О₁, через которую проводят ось цилиндра параллельно изометрической оси х. От точки О₁ по этой оси откладывают координату х = О₁О₂ точки О₂ — центра окружности основания цилиндра.

Для построения линии пересечения находят изометрические проекции точек этой линии с помощью их координат, взятых с комплексного чертежа. За начало координат принимается точка О₂ (центр основания цилиндра). Параллельно оси у проводят до пересечения с овалом следы плос­костей сечения с координатами по оси z, взятых с профильной проекции. Из полученных точек А, В, С. параллельно оси х проводят прямые — об­разующие цилиндра, на них откладывают ко­ординаты Al, В2, . взятые с фронтальной проекции комплексного чертежа, и получают точки 2. 12, принадлежащие искомой линии пере­сечения.

Через найденные точки проводят кривую ли­нию по лекалу.

На рис. 210 показана деталь. Линию пересечения конической поверхности с цилиндрической строят описанным выше спосо­бом.

Построение линии пересечения поверхностей цилиндра и конуса, оси которых параллельны (рис. 211), аналогично построению, рассмотренно­му на рис. 209.

Выбирают вспомогательные горизонтальные плоскости, например Р₁, Р₂ и Р₃, которые пересекают конус и цилиндр по окружностям (рис. 211, б). Диаметр окружностей, образованных в результате пересечения этих плоскостей с ци­линдрам, одинаков и равен D; диаметры окруж­ностей, полученных в результате пересечения плоскостей с конусом, — различные. Взаимное пересечение горизонтальных проекций этих ок­ружностей дают искомые горизонтальные проек­ции точек 1. 9 линии пересечения (рис. 211, а). Фронтальные проекции 1′. 9′ этих точек находят с помощью линий связи на фронтальных следах Р_V1, Р_V2, Р_V3 вспомогательных плоскостей. Про­фильные проекции точек строят по двум их извес­тным проекциям.

Характерными точками в данном примере явля­ются: высшая точка линии пересечения — точка 5, нахождение проекций которой начинают с име­ющейся горизонтальной проекции, и точки 1, 9

Точки 1 и 9 получились от пересечения основа­ний цилиндра и конуса.

Построение изометрической проекции пересекающихся конуса и цилиндра (рис. 211, в) выполня­ется по этапам, подробно описанным в предыдущем примере (см. рис. 209, в). Построение начи­нается проведением изометрических осей конуса и цилиндра, затем их оснований (эллипсов) с центрами на расстоянии друг от друга, определяе­мом координатой n₃. Для построения линий пере­сечения находят изометрические проекции точек этой линии с помощью координат, взятых с чер­тежа.

На рис. 212 показана деталь, имеющая форму двух цилиндров, пересекающихся с конусом. Оси цилиндра и конуса параллельны.

Примеры пересечения поверхностей даны на рис. 213. Линии пересечения показаны красным цветом.

Видео:Виды и изометрия цилиндраСкачать

Пересечение поверхностей сферы и цилиндра

Прямой круговой цилиндр, расположенный перпендикулярно плоскости Н, пересекается с шаром, центр которого расположен на оси цилин­дра, по окружности, которая изображается на фронтальной проекции отрезком прямой (рис 214). Проводя через точки А и В пересече­ния контурных образующих цилиндра и очерка шара вспомогательную горизонтальную плоскость Р, заметим следующее. Плоскость Р пересечет как цилиндр, так и шар по окружности одинакового диаметра, которая расположена в проецирующей плоскости. Следовательно, се фронтальная проек­ция будет изображаться в виде прямой а’b’.

При пересечении поверхности конуса или по­верхности вращения с шаром, центр которого расположен на оси этих поверхностей, также по­лучается окружность (рис. 214, а).

Если центр шара расположен вне оси цилиндра (рис. 214, б), то для построения линии пересече­ния применяют вспомогательные горизонтальные плоскости. Например, вспомогательная горизонтальная плоскость Р пересекает цилиндр по ок­ружности радиуса r, а шар — по окружности ради­уса R. Точки пересечения а и b горизонтальных проекций этих окружностей принадлежат горизонтальной проекции линии пересечения. Фронтальные проекции а’ и b‘ строят, используя ли­нии связи.

Одной из характерных точек данной линии пересечения является верхняя точка D. Горизон­тальная проекция этой точки находится на пере­сечении прямой, соединяющей центры окружнос­тей радиусов r и R с горизонтальной проекцией основания цилиндрической поверхности. Для по­строения фронтальной проекции точки D через точку d проводят дугу радиуса r₁, строят фрон­тальную проекцию дуги (отрезок прямой, парал­лельной оси х) и с помощью линии связи находят точку d’.

Видео:Часть 1. Изометрическая проекция. (стр. 29)Скачать

Пересечение поверхностей тора и цилиндра

Патрубок, форма которого образована пересека­ющимися поверхностями тора и цилиндра, пока­зан на рис. 215. Выполнен комплексный чертеж с построением линии пересечения поверхностей и тора, и цилиндра. В этом примере очевидные точки 1 и 5. Для определения проекций промежу­точных точек используют вспомогательные плос­кости Р_Н и P_Н1, параллельные фронтальной плос­кости проекции. Например, плоскость Р_Н пересе­кает поверхность тора по окружности радиуса R, а поверхность цилиндра — по двум образующим Взаимное пересечение этих образующих с дугою окружности радиуса R дает на фронтальной про­екции две точки 2′ и 4′, принадлежащие искомой линии пересечения.

Видео:Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Построение линий пересечения поверхностей способом вспомогательных сфер

Для построения линии пересечения поверхнос­тей вместо вспомогательных секущих плоскостей при определенных условиях удобно применять вспомогательные сферические поверхности.

В отличие от метода вспомогательных секущих плоскостей метод вспомогательных сфер имеет преимущество, так как при построении фронтальной проекции линии пересечения поверхностей не используются две другие проекции пересекающих­ся поверхностей (рис. 216).

Вспомогательные сферические поверхности для построения линий пересечения поверхностей тел можно применять лишь при следующих условиях:

а) пересекающиеся поверхности должны быть поверхностями вращения;

б) оси поверхностей вращения должны пересе­каться; точка пересечения осей является центром вспомогательных сфер;

в) оси поверхностей вращения должны быть параллельны какой-либо плоскости проекций.

Примеры применения вспомогательных сфери­ческих поверхностей показаны на рис. 216, а и б.

На рис. 216, а дано построение фронтальных проекций линии пересечения поверхностей двух цилиндров, оси которых пересекаются под острым углом.

Вспомогательные сферические поверхности проводят из точки О’ пересечения осей цилин­дров.

Построим, например, фронтальную проекцию некоторой промежуточной точки линии пересече­ния. Для этого из точки О’ проводят сферичес­кую поверхность радиуса R, которая на данной проекции изобразится в виде окружности этого же радиуса. Окружность радиуса R пересечет горизонтальный цилиндр по окружностям диаметра АС и ВD, а наклонно расположенный цилиндр — по окружностям диаметра АВ.

В пересечении полученных проекций окружнос­тей — отрезков а’b’ и c‘d‘— находят проекцию 2′ промежуточной точки линии пересечения.

Вводя еще целый ряд вспомогательных сфери­ческих поверхностей, можно построить необходи­мое число точек линии пересечения.

Пределы радиусов сферических поверхностей находят следующим образом (рис. 216, а и б): наибольшая окружность сферической поверхности должна пересекаться с контурными образующими 1—1 и II— II цилиндра и наименьшая должна быть касательной к одной из данных пересекающихся поверхностей и пересекаться с образующими дру­гой поверхности.

Если поверхности двух конусов (рис. 217, а) описаны около шара, то они касаются шара по двум окружностям; эти окружности пересекаются в двух точках, которые проецируются на фрон­тальную плоскость проекций в точку р’. Плоскости, в которых лежат эти окружности, пересекают­ся по прямой, соединяющей точки пересечения линий касания конусов с шаром. Окружности проецируются на фронтальную плоскость проек­ций в виде прямых линий.

Соединив очевидную точку s’ пересечения конусов с точкой р‘, получим линию пересечения конусов с шаром, которая представляет собой фронтальную проекцию эллипса.

Разберем второй подобный пример. Если два прямых круговых цилиндра с осями, пересекаю­щимися в точке О’ (рис. 217, б), описаны около шара с центром в точке О, то фронтальная про­екция шара будет окружностью, касательной к контурным образующим цилиндров. Линии пере­сечения поверхностей этих цилиндров представля­ют собой эллипсы, фронтальные проекции кото­рых изображаются в виде прямых линий а’b‘ и c’d’.

Примеры и образцы решения задач:

Услуги по выполнению чертежей:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.