Движение шарика в наклонном цилиндре (3 видео)

Содержание

Лабораторная работа № 1 «Измерение ускорения тела при равноускоренном движении»
Решебник по физике за 9 класс Кикоин: решения задач, самое важное и лабораторные работы
Исследование скатывания тел по наклонной плоскости
💡 Видео

Видео:Шарик в струеСкачать

Лабораторная работа № 1 «Измерение ускорения тела при равноускоренном движении»

Цель работы: вычислить ускорение, с которым скатывается шарик по наклонному желобу. Для этого измеряют длину перемещения s шарика за известное время t. Так как при равноускоренном движении без начальной скорости

то, измерив s и t, можно найти ускорение шарика. Оно равно:

Никакие измерения не делаются абсолютно точно. Они всегда производятся с некоторой погрешностью, связанной с несовершенством средств измерения и другими причинами. Но и при наличии погрешностей имеется несколько способов проведения достоверных измерений. Наиболее простой из них — вычисление среднего арифметического из результатов нескольких независимых измерений одной и той же величины, если условия опыта не изменяются. Это и предлагается сделать в работе.

Средства измерения: 1) измерительная лента; 2) метроном.

Материалы: 1) желоб; 2) шарик; 3) штатив с муфтами и лапкой; 4) металлический цилиндр.

Порядок выполнения работы

1. Укрепите желоб с помощью штатива в наклонном положении под небольшим углом к горизонту (рис. 175). У нижнего конца желоба положите в него металлический цилиндр.

2. Пустив шарик (одновременно с ударом метронома) с верхнего конца желоба, подсчитайте число ударов метронома до столкновения шарика с цилиндром. Опыт удобно проводить при 120 ударах метронома в минуту.

3. Меняя угол наклона желоба к горизонту и производя небольшие передвижения металлического цилиндра, добивайтесь того, чтобы между моментом пуска шарика и моментом его столкновения с цилиндром было 4 удара метронома (3 промежутка между ударами).

4. Вычислите время движения шарика.

5. С помощью измерительной ленты определите длину перемещения s шарика. Не меняя наклона желоба (условия опыта должны оставаться неизменными), повторите опыт пять раз, добиваясь снова совпадения четвертого удара метронома с ударом шарика о металлический цилиндр (цилиндр для этого можно немного передвигать).

найдите среднее значение модуля перемещения, а затем рассчитайте среднее значение модуля ускорения:

7. Результаты измерений и вычислений занесите в таблицу:

Видео:Скатывание цилиндров с наклонной плоскостиСкачать

Решебник по физике за 9 класс Кикоин: решения задач, самое важное и лабораторные работы

Лабораторная работа № 1 «Измерение ускорения тела при равноускоренном движении».

то, измерив s и t, можно найти ускорение шарика. Оно равно:

Средства измерения: 1) измерительная лента; 2) метроном.

Материалы: 1) желоб; 2) шарик; 3) штатив с муфтами и лапкой; 4) металлический цилиндр.

Порядок выполнения работы

4. Вычислите время движения шарика.

найдите среднее значение модуля перемещения, а затем рассчитайте среднее значение модуля ускорения:

7. Результаты измерений и вычислений занесите в таблицу:

При прямолинейном равноускоренном движении без начальной скорости

где S — путь, пройденный телом, t — время прохождения пути. Средства измерения: измерительная лента (линейка), метроном (секундомер).

Лабораторная установка и порядок выполнения работы подробно описаны в учебнике.

№ опыта	t, с	S, м
1	6	0,5	0,028
2	5,5	0,5	0,033

3	5	0,49	0,039
4	5,5	0,49	0,032
5	6,5	0,51	0,024
среднее значение	5,7	0,5	0,03

Точность приборов: Измерительная лента:

Вычислим абсолютные погрешности:

Читайте также: Задир зеркала цилиндра как быть

Вычислим относительную погрешность:

Абсолютная погрешность косвенного измерения:

Найденное в результате работы ускорение можно записать так:

но при данной абсолютной погрешности последняя цифра в значении а_ср значения не имеет, поэтому запишем так:

Шаблоны Инстаграм БЕСПЛАТНО

Хотите получить БЕСПЛАТНЫЙ набор шаблонов для красивого Инстаграма?

Напишите моему чат-помощнику в Telegram ниже ?

Вы получите: ? Бесплатные шаблоны «Bezh», «Akvarel», «Gold»

или пишите «Хочу бесплатные шаблоны» в директ Инстаграм @shablonoved.ru

Шаблоны Инстаграм БЕСПЛАТНО

Хотите получить БЕСПЛАТНЫЙ набор шаблонов для красивого Инстаграма?

Напишите моему чат-помощнику в Telegram ниже ?

Вы получите: ? Бесплатные шаблоны «Bezh», «Akvarel», «Gold»

Видео:Столкновение шаров на уголковом желобеСкачать

Исследование скатывания тел по наклонной плоскости

Исследование скатывания тел по наклонной плоскости

Цель работы: приобрести некоторые навыки самостоятельного исследования физических явлений и обработки полученных результатов.

Оборудование и принадлежности: наклонная плоскость (трибометр), линейка масштабная, набор тел, весы, секундомер.

Задание. Исследовать скатывание цилиндров и шара по наклонной плоскости.

Примечание: если цилиндр или шар скатывается по наклонной плоскости, расположенной под небольшим углом к горизонту, то скатывание происходит без проскальзывания. Если угол наклона плоскости превысит некоторое предельное значение, то скатывание будет происходить с проскальзыванием.

При выполнении задания необходимо определить тот предельный угол, при котором скатывание тел начнет происходить с проскальзыванием. По результатам исследования составить отчет, в котором отразить методику исследования, предоставить таблицу результатов наблюдений и дать объяснение, почему при угле, превышающем некоторое значение, скатывание тел происходит с проскальзыванием.

Кроме того, в задачу входит определение момента инерции цилиндров и шара no результатам наблюдений скатывания их с наклонной плоскости.

Краткая теория

Положим, цилиндр катится по наклонной плоскости без скольжения. На цилиндр действуют внешние силы: сила тяжести , сила трения , и сила реакции со стороны плоскости . Движение рассматриваем как поступательное со скоростью, равной скорости центра масс, и вращательное относительно оси, проходящей через центр масс.

Уравнение для движения центра масс шара (цилиндра)

или в скалярном виде в проекциях:

Уравнение моментов относительно оси

При отсутствии проскальзывания

Найдем ускорение, которое приобретает цилиндр под действием указанных сил. Оно может быть найдено путем использования выражения для кинетической энергии катящегося тела

где — масса шара (цилиндра), — скорость поступательного движения центра масс, — момент инерции шара, относительно оси вращения, — угловая скорость вращения, относительно оси вращения.

Изменение кинетической энергии тела равно работе внешних сил, действующих на тело. Элементарная работа силы трения и реакции, плоскости равна нулю, т.к. линии действия их проходят через мгновенную ось вращения ( ). Следовательно, изменение кинетической энергии тела происходит только за счёт работы силы тяжести

или проинтегрировав выражение (2) в пределах от до , получим,

где — кинетическая энергия тела в конце наклонной плоскости, — начальная энергия (кинетическая) тела, ; — длина наклонной плоскости, тогда энергия тела

(3)

(4)

Поступательное движение тела по наклонной плоскости происходит равноускоренно, поэтому можно записать

где — конечная скорость центра масс в конце наклонной плоскости, — начальная скорость, она равна нулю, поэтому

(6)

(7)

Выражение (4) с учетом (6) и (7) может быть записано

где – ускорение поступательного движения тела при скатывании по наклонной плоскости.

Так как это равноускоренное движение с начальной скоростью , то можно записать или , подставляя значение а в (8) окончательно получим

где — время скатывания тела по наклонной плоскости, — радиус шара (цилиндра), — масса шара (цилиндра), — угол наклона плоскости к горизонту, — длина наклонной плоскости.

Измерив указанные выше величины, можно вычислить момент инерции скатывающегося цилиндра. Он может быть сплошным, пустотелым, с канавками на его образующей поверхности и т.д. Формула (9): справедлива и для цилиндров и для шара.

Эксперимент с каждым из тел проводить не менее трех раз. Результаты наблюдений и вычислений занести в таблицу 1.

№ п/п

Форма скатывающегося тела

Масса , кг

Радиус , м

Длина наклонной плоскости (м)

Время скатывания, с

Момент инерции , кг·м 2

Определить для каждого случая погрешность при определении .

Определите значение момента инерции для каждого тела теоретически. Сравните значение момента инерции тел определенных теоретически и из эксперимента и в случае их несовпадения объясните причину.

1. Дать определение момента сил. Записать в векторной форме. Как направлен момент сил относительно силы? Что такое радиус-вектор действия силы? Нарисовать и показать на рисунке.

2.Какое направление имеют угловое ускорение, угловая скорость?

3. Дать определение момента инерции материальной точки и абсолютно твердого тела. Физический смысл инерции.

Читайте также: Рабочий цилиндр сцепления газель фенокс

4. Вывести момент инерции шара и цилиндра.

5. Доказать теорему Штейнера.

6. Сформулировать закон сохранения энергии при вращательном движении.

7. Вывести формулу дня расчета кинетической энергии с учетом вращения тела.

8. Вывести закон сохранения момента импульса системы тел.

9. Дать определение центра масс системы теп.

10.Сформулировать условие, при которых тело скатывается без проскальзывания и вывести формулы, используемые в расчете.

11.Сформулировать законы динамики для вращательного движения и вывести их для .материальной точки и для абсолютно твердого тела.

12.Объясните, как рассчитывали погрешность измерений в работе.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1) Трофимова Т.И. Курс физики: учебное пособие для инженерно-технических специальностей вузов — М.: Academia, 2006.

2) Александров И.В. и др. Современная физика [Электронный ресурс]: учебное пособие для студентов всех форм обучения, обучающихся по техническим и технологическим направлениям и специальностям — Уфа: УГАТУ, 2008.

3) Гринкруг М.С., Вакулюк А.А. Лабораторный практикум по физике [Электронный ресурс] — СПб: Лань, 2012.

4) Калашников Н. П. Основы физики: учебник для вузов: в 2-х т / Н. П. Калашников, М. А. Смондырев — М.: Дрофа, 2007.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФИЛИАЛ ФГБОУ ВПО «УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Методические указания

к лабораторной работе по курсу общей физики

раздел: раздел: «Механика. Механические колебания. Статистическая физика и термодинамика»

ЛАБОРАТОРНАЯ РАБОТА № 9

Определение коэффициента
внутреннего трения жидкостей

Цель работы: определить коэффициент внутреннего трения неизвестной жидкости по методу Стокса.

Приборы и оборудование: стеклянный цилиндр с исследуемой жидкостью, секундомер, шарики разного диаметра, микрометр.

Краткая теория

На всякое тело, двигающееся в вязкой жидкости, действует сила сопротивления. В общем случае величина этой силы зависит от многих факторов: от внутреннего трения жидкости, от формы тела, от характера обтекания и т.д.

Сила внутреннего трения, возникающая при макроскопических движениях в жидкости, прямо пропорциональна градиенту скорости. Коэффициент пропорциональности носит название коэффициента внутреннего трения, или просто вязкости жидкости. Вязкость (или динамическая вязкость) численно равна силе внутреннего трения, действующей на единицу площади границы раздела параллельно движущихся слоев жидкости, когда скорость их движения уменьшается на единицу при перемещении в направлении, перпендикулярном к границе, на единицу длины, т.е.

Закон (1) был получен Ньютоном из анализа экспериментальных данных и явился основой при изучении движения вязкой жидкости и газа.

Рассмотрим для примера равномерное движение маленького шарика радиуса вжидкости.

Обозначим скорость шарика относительно жидкости через .

Распределение скоростей в соседних слоях жидкости, увлекаемых шариком, должно иметь вид, изображенный на рисунке 1. В непосредственной близости к поверхности шара эта скорость равна , а по мере удаления уменьшается и практически становится равной нулю на некотором расстоянии от поверхности. Очевидно, что чем больше радиус шара, тем больше масса жидкости вовлекается им в движение, и должно быть пропорционально

Величина коэффициента пропорциональности в (2), вообще говоря, несколько различна для передней и задней частей движущегося тела, и под мы будем понимать среднее значение этого коэффициента. Тогда среднее значение градиента скорости по поверхности шара равно:

Поверхность шара и полная сила трения, испытываемая движущимся шаром, равна

Интегрирование уравнений движения вязкой жидкости, проведенное Стоксом, дало для шара значение . Следовательно, сила сопротивления, испытываемая шаром, движущимся в вязкой жидкости, прямо пропорциональна вязкости , радиусу шара , скорости его движения :

Формула (5) носит название закона Стокса.

Формула Стокса применима лишь в случае тел достаточно малых размеров и малых скоростей их движения. При больших скоростях вокруг движущихся тел возникают сложные вихревые движения жидкости, и сила сопротивления возрастает пропорционально квадрату скорости, а не первой его степени.

Роль трения характеризуется безразмерной величиной, называемой числом Рейнольдса :

где — линейные размеры, характерные для рассматриваемого течения жидкости. В случае течения жидкости по трубе — радиус трубы, — средняя скорость. Отношение называется кинематическим коэффициентом вязкости.

Для того, чтобы пояснить роль числа Рейнольдса, рассмотрим элемент объема жидкости с длиной ребра . Кинетическая энергия этого объема равна:

Сила трения, действующая на элемент объема жидкости, пропорциональна его поверхности , коэффициенту вязкости и градиенту скорости. Полагая, что скорость падает до нуля на расстоянии равном по порядку величины (в случае течения по трубе – в радиальном направлении), получим, что градиент скорости равен . Таким образом, сила трения

Работа этой силы на пути равна

Роль трения при течении жидкости мала, если работа мала по сравнению с кинетической энергией объема жидкости , то есть если выполняется неравенство

Но — Re есть число Рейнольдса.

Таким образом, роль сил трения при течении жидкости мала при больших числах Рейнольдса.

Читайте также: Блок отключения цилиндров хонда пилот

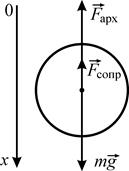
Рассмотрим свободное падение шарика в вязкой жидкости.На шарик действует 3 силы: сила тяжести, архимедова сила, сила сопротивления, зависящая от скорости. Найдем уравнение движения шарика в жидкости.По второму закону Ньютона

Проецируя силы на ось , получим:

где — объем шарика; — его плотность; — плотность жидкости; — ускорение силы тяжести.

Решая это уравнение, найдем

В формуле (7) приняты обозначения: – скорость шарика в момент начала его движения в жидкости, т.к. у нас скорость установившаяся, то ускорение шарика равно нулю, и из уравнения (6) следует:

Как видно из (7), скорость шарика экспоненциально приближается к установившейся скорости . Установление скорости определяется величиной , имеющей размерность времени и называющейся временем релаксации. Если время падения в несколько раз больше времени релаксации, процесс установления скорости можно считать закончившимся.

Измеряя на опыте установившуюся скорость падения шарика и величины , можно определить коэффициент внутреннего трения жидкости по формуле

Указание: шарики с разными радиусами движутся в жидкости с равными скоростями и с разными временами релаксации. Если во всем диапазоне встречающихся скоростей и времен релаксации вычисленные по формуле (10) значения оказываются одинаковыми то формула (5) правильно передает зависимость сил от радиуса шарика. Зависимость или независимость от служит чувствительным индикатором правильности теории и надежности эксперимента. Результаты опыта имеет смысл обрабатывать лишь в том случае, если значение не обнаруживает систематической зависимости от . Если такая зависимость наблюдается, то чаще всего это связано с влиянием стенок сосуда.

В этом случае следует использовать более точную формулу:

где – радиус сосуда.

Задание 1. Вычисление плотности шариков.

1. С помощью микрометра определить диаметр шарика.

2. Произвести измерения не менее трех раз для каждого шарика.

3. Вычислить средние значения диаметров шариков.

4. С помощью весов определить массы шариков.

6. Вычислить плотность по формуле: .

7. Результат занести в таблицу 1.

, м	, м	, м	, м	, м	, м 3	, кг	, кг/м 3	, кг/м 3
1.
2.
3.

Задание 2. Вычисление коэффициента вязкости.

1. С помощью электронного секундомера измерить время падения шарика от верхней метки до нижней.

2. Провести измерения не менее трех раз.

3. Вычислить среднее значение времени падения шарика.

4. Вычислить среднее значение по формуле: , где — расстояние от верхней до нижней меток.

6. Вычислить среднее значение по формуле (10).

7. Результаты занести в таблицу 2.

, с	, с	, с	, с	, м/с	, Па·с	, Па·с
1.
2.
3.

1. Вывести уравнение Бернулли, Пуазейля, Стокса.

2. Что такое коэффициент внутреннего трения? Динамическая и кинематическая вязкости и их связь между собой.

3. Что характеризует собой число Рейнольдса?

4. Ламинарное и турбулентное течение и их связь с числом Рейнольдса.

5. Каковы границы применимости закона Стокса?

6. Какие методы определения силы трения существуют?

7. Как объяснить механизм явления вязкого трения?

8. От каких физических величин зависит трение?

9. Какие преобразования энергии происходят при движении тел с учетом силы трения?

10. Чему равна величина силы трения покоя, скольжения?

11. Расскажите о трении скольжения, покоя, вязкого трения и трения качения.

12. Почему трение скольжения больше трения качения?

13. Почему вязкое трение меньше трения скольжения?

14. Как трение проявляется в природе? Когда оно играет положительную, отрицательную роль? Как избавиться от трения?

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1) Трофимова Т.И. Курс физики: учебное пособие для инженерно-технических специальностей вузов — М.: Academia, 2006.

3) Гринкруг М.С., Вакулюк А.А. Лабораторный практикум по физике [Электронный ресурс] — СПб: Лань, 2012.

4) Калашников Н. П. Основы физики: учебник для вузов: в 2-х т / Н. П. Калашников, М. А. Смондырев — М.: Дрофа, 2007.

ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования.

Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот.

Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право.