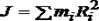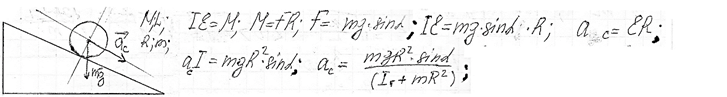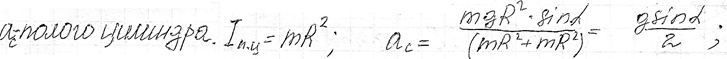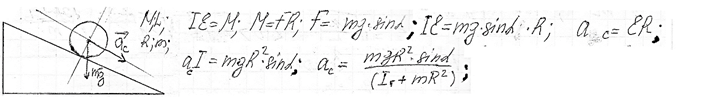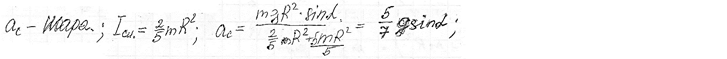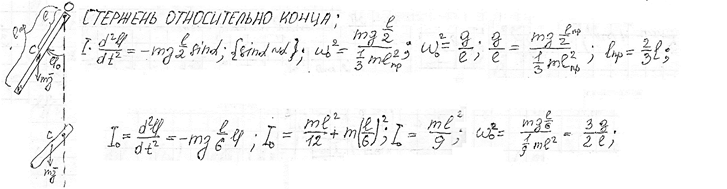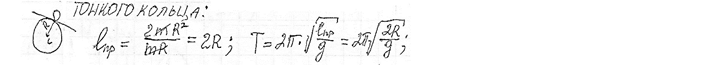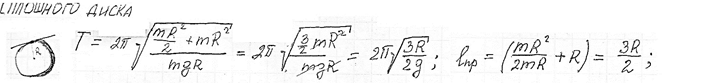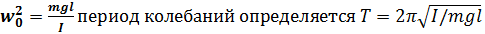Движение центра масс цилиндра (8 видео)

Момент инерции твердого тела. Теорема Штейнера. Основное уравнение вращательного движения. Ускорение центра масс полого цилиндра, скатывающегося с наклонной плоскости.

Момент инерции твердого тела.

Видео:Скатывание цилиндров с наклонной плоскостиСкачать

— является моментом инерции тела относительно оси вращения. (посмотреть вывод)

теорема Штейнера: момент инерции J тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела J_C относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями

Видео:Задача на теорему о движении центра массСкачать

Ускорение центра масса полого цилиндра

Ускорение центра масс (по теореме о движении центра масс) определяется суммой внешних по отношению к системе сил, если считать их приложенными к некоторой эквивалентной материальной точке, которая помещена в центр масс и имеет массу.

(посмотреть вывод в допах или лекциях «Движение твердого тела»)

Видео:Движение центра масс системы телСкачать

12. Момент инерции твердого тела. Теорема Штейнера. Основное уравнение динамики вращательного движения. Ускорение центра масс сплошного цилиндра, скатывающегося с наклонной плоскости.

Видео:Движение центра масс твердого телаСкачать

13. Момент инерции твердого тела. Теорема Штейнера. Основное уравнение динамики вращательного движения. Ускорение центра масс шара, скатывающегося с наклонной плоскости.

Физический маятник. Уравнение движения физического маятника. Приведенная длина физического маятника. Период колебаний и приведенная длина однородного стержня, качающегося в поле силы тяжести.

Видео:Скатывание тела (колеса, цилиндра) по наклонной плоскостиСкачать

Физический маятник. Уравнение движения физического маятника. Приведенная длина физического маятника. Период колебаний и приведенная длина тонкого кольца, качающегося в поле силы тяжести.

Физический маятник. Уравнение движения физического маятника. Приведенная длина физического маятника. Период колебаний и приведенная длина сплошного диска, качающегося в поле силы тяжести.

Видео:3.3. Центр масс и закон его движения | Динамика | Александр Чирцов | ЛекториумСкачать

Физический маятник. Уравнение движения физического маятника. Приведенная длина физического маятника. Период колебаний и приведенная длина однородного шара, качающегося в поле силы тяжести.

17.1. Физический маятник – твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной. При отклонении маятника на α (рис. 7.4) возникает вращательный момент, стремящийся вернуть маятник в положение равновесия: расстояние между точкой подвеса О и центром масс С. Знак «– » ставиться потому что при отклонении маятника возникает вращательный момент который пытается вернуть его в положение равновесия и аналогичен в этом случае квазиупругой силе. Поэтому так же, как смещению и квазиупругой силе, моменту N и угловому смещению нужно приписать противоположные знаки.

17.2. Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, буквой I, можно написать уравнение динамики вращательного движения: при малых колебаниях уравнение имеет вид: Из данных уравнений следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, чатсота которых зависит от массы, момента инерции относительно оси вращения и расстоянию между оси вращения и центром масс маятника. В соответствии с 17.3. Из сопоставления формул периода колебаний математического и физического маятника получается что математический маятник длинной будет иметь период колебаний как и физический маятник. Данную величину называют приведенной длинной физического маятника – это длина такого математического маятника, период колебания которого совпадает с периодом данного физического маятника. Центр качения физического маятника (точка – точка на прямой соединяющая точку подвеса с центром масс, лежащая на расстоянии приведенной длинны от оси вращения.

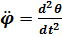
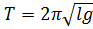
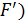
При подвешивания маятника в центре качения период и приведенная длинна сохраняется, а значит точка подвеса и центр качения обладают свойством взаимности (при переносе точки подвеса в центр качения прежняя точка становиться новым центром качения) 17.4.