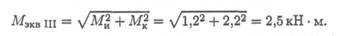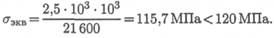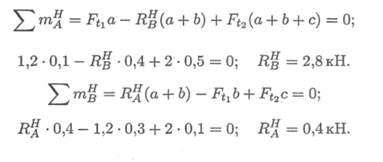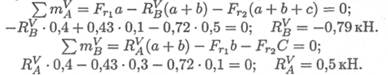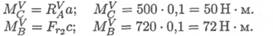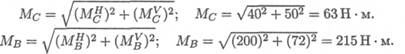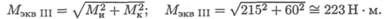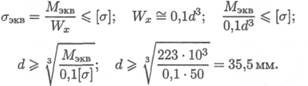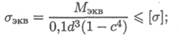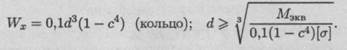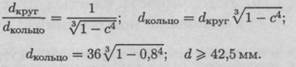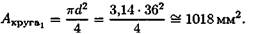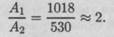В предыдущей статье мы рассматривали случаи сочетания основных деформаций, когда в поперечных сечениях бруса возникают только нормальные напряжения, и суммарное напряжение в каждой точке можно было рассчитать простым алгебраическим сложением. Однако часто имеют место случаи сочетания основных деформаций, при которых в поперечных сечениях возникают и нормальные, и касательные напряжения, распределенные по площади сечений неравномерно и по разным законам.
Для таких случаев опытное определение величин, характеризующих прочность, невозможно, поэтому при оценке прочности детали приходится основываться на механических характеристиках данного материала, полученных из диаграммы растяжения.
Как известно, при растяжении прочность пластичных материалов характеризуется пределом текучести, а прочность хрупких материалов – пределом прочности. Эти напряжения считаются предельными, и в зависимости от их величины вычисляют допускаемые напряжения. Для упрощения расчетов величины напряжений при сочетании деформаций вводят понятие эквивалентного (равноопасного) напряжения.
Напряженные состояния при сочетании основных деформаций и одноосном растяжении называют равноопасными или эквивалентными, если их главные напряжения отличаются от предельного для данного материала в одинаковое число раз, т. е. коэффициенты запаса прочности для эквивалентных напряжений одинаковы.
Иными словами, эквивалентным считается такое напряжение при простом одноосном растяжении, которое равноопасно данному сочетанию основных деформаций.
Таким образом, условие прочности при сочетании основных деформаций, когда в поперечных сечениях действуют и нормальные и касательные напряжения, будет иметь вид: σэкв ≤ [σp] .
Формулы для определения эквивалентных напряжений, которые затем сопоставляют с предельно допускаемыми, выводят на основании гипотез прочности.
Гипотезы прочности – это научные предположения об основной причине достижения материалом предельного напряженного состояния при сочетании основных деформаций.
В настоящее время при вычислении эквивалентных напряжений используют три гипотезы прочности: гипотезу наибольших касательных напряжений (или третья гипотеза прочности), гипотезу Мора (четвертая гипотеза прочности) и энергетическую гипотезу (пятая гипотеза прочности).
Применявшиеся ранее при расчетах первая (гипотеза Галилея) и вторая (гипотеза Мариотта-Сен-Венана) гипотезы прочности, основанные соответственно на наибольших нормальных напряжениях и линейных деформациях, в настоящее время не используются, поскольку плохо подтверждаются опытами.
Рассмотрим подробнее суть каждой из перечисленных гипотез прочности.
Третья теория прочности
Гипотеза наибольших касательных напряжений
Согласно этой гипотезе, предложенной в конце XVIII в., опасное состояние материала наступает тогда, когда наибольшие касательные напряжения достигают предельной величины.
Если рассмотреть элементарную площадку в наклонном сечении продольно растягиваемого бруса, то при помощи простых геометрических выкладок можно убедиться, что касательное напряжение в такой площадке достигает максимальной величины, когда сечение располагается под углом 45˚ к оси бруса. При этом величина касательного напряжения будет равна половине разности между максимальным и минимальным нормальным напряжением:
В частном случае, если σmin = 0 , то τmax = σmax/2 .
Чтобы вывести формулу для вычисления эквивалентных напряжений по третьей теории прочности, рассмотрим брус, у которого в поперечном сечении действуют нормальные σ и касательные τ напряжения (см. рисунок) .
Внутри бруса вблизи от произвольной точки В вырежем бесконечно малую призму abc , у которой грань ab совпадает с поперечным, грань ac – с продольным сечениями, а грань bc является главной площадкой, на которой действует главное напряжение σ0 .
Согласно закону парности касательных напряжений в грани ac призмы также будут действовать касательные напряжения τ .
Поскольку в продольном сечении бруса нормальных напряжений нет, то здесь мы имеем дело со случаем плоского напряженного состояния, который называют упрощенным.
Рассмотрим равновесие призмы abc , для чего спроецируем все действующие на нее силы на оси z и y . Площадь грани bc обозначим dA (элементарная площадка). Тогда:
Читайте также: Компрессор из двс ваз 2108 своими руками
Σ Z = 0; σ0 dAsinφ — τ dA cosφ — σ dA sinφ = 0
Σ Y = 0; σ0 dA cosφ — τ dA sinφ = 0 .
Разделив обе части равенства на dA , получим:
(σ0 – σ) sinφ = τ cosφ; σ0 cosφ = τ sinφ .
Оба равенства разделим на cosφ и, исключив из них tgφ , получим выражение:
τ / (σ0 — σ) = σ0 / τ , что равнозначно квадратному уравнению σ0 2 — σ0σ – τ 2 = 0 .
Решая это уравнение, получим:
(Здесь и далее знак √ обозначает квадратный корень).
Таким образом, главные напряжения в наклонных площадках в зонах точки А бруса определяют по формулам:
σmax = σ/2 + 1/2 √(σ 2 + 4τ 2 ) σmin = σ/2 — 1/2 √(σ 2 + 4τ 2 ) .
Следовательно, исходя из формулы (1) , максимальные касательные напряжения можно найти по формуле:
Поскольку τпред = σпред/2 , а эквивалентное напряжение не должно превышать предельного, то, применяя гипотезу наибольших касательных напряжений, имеем:
В результате мы получили формулу для вычисления эквивалентных напряжений:
Гипотеза наибольших касательных напряжений хорошо подтверждается опытами, в особенности для пластичных материалов.
Четвертая теория прочности
Гипотеза Мора
Большой вклад в разработке методов определения напряжений при сложном напряженном состоянии внес немецкий ученый Кристиан Отто Мор (Christian Otto Mohr, 1835-1918 г.г.) .
Заслуги К.О.Мора в науке сопротивление материалов трудно переоценить — он является создателем одной из теорий прочности (теория прочности Мора), графических методов определения напряжений при сложном напряжённом состоянии (круг Мора).
Мор впервые применил расчёт конструкций на невыгодное загружение с помощью так называемых линий влияния, создал теорию расчёта статически неопределимых систем методом сил. Этот ученый разработал также метод расчёта неразрезных балок с помощью уравнений трех моментов, предложил графический метод построения упругой линии в простых и неразрезных балках.
Гипотеза Мора, предложенная им в начале XX века может быть сформулирована так:
Опасное состояние материала наступает тогда, когда на некоторой площадке осуществляется наиболее неблагоприятная комбинация нормального и касательного напряжений.
По сути, это усовершенствованная и обобщенная гипотеза наибольших касательных напряжений, рассмотренная ранее, тем не менее, она дает возможность определять эквивалентные напряжения в балках с меньшей степенью погрешности и применима при расчетах на прочность как пластичных, так и хрупких материалов.
Формула для вычисления эквивалентных напряжений, согласно гипотезе Мора имеет вид:
σэкв = σ(1 – k)/2 + 1/2 (1 + k) √(σ 2 + 4τ 2 ) ,
Очевидно, что при k = 1 формула Мора тождественна формуле третьей теории прочности (гипотезе наибольших касательных напряжений).
Пятая, или энергетическая теория прочности
Энергетическая гипотеза
При деформации элементарной частицы тела в общем случае изменяются ее форма и объем. Таким образом, полная потенциальная энергия деформации состоит из двух частей: энергии формоизменения и энергии изменения объема.
Энергетическая гипотеза прочности, предложенная в начале XX века в качестве критерия перехода материала в предельное состояние принимает только энергию формоизменения.
Согласно этой гипотезе, опасное состояние материала в данной точке наступает тогда, когда удельная потенциальная энергия формоизменения для этой точки достигает предельной величины.
Формула для вычисления эквивалентных напряжений в соответствии с пятой (энергетической) теорией прочности имеет вид:
Эта формула хорошо подтверждается опытным путем для пластичных материалов и получила широкое распространение.
Следует отметить, что во всех приведенных выше формулах σ и τ — нормальные и касательные напряжения на площадке поперечного сечения, проходящего через опасную или предположительно опасную точку.
Видео:Понимание напряжений в балкахСкачать
Электронная библиотека
Применение теорий прочности позволяет рассчитывать валы на совместное действие изгиба и кручения. Валы изготавливают, как правило, из среднеуглеродистых конструкционных или легированных сталей, одинаково сопротивляющихся деформациям растяжения и сжатия. Поэтому расчет выполняется на основе третьей (по критерию наибольших касательных напряжений) или четвертой (по критерию удельной потенциальной энергии формоизменения) теорий прочности, в соответствии с которыми эквивалентные напряжения определяются по формулам:
Читайте также: Контроль допуска цилиндричности валов
где , – напряжения в точках контура поперечного сечения вала, соответственно, от деформаций изгиба и кручения; – допускаемое напряжение, МПа.
Напряжения в точках контура вала (в мегапаскалях) определяются по формулам:
где , – соответственно, результирующий изгибающий и крутящий моменты в опасном сечении вала, Н·мм; , – соответственно осевой и полярный моменты сопротивления сечений вала, мм 4 .
Моменты сопротивления определяются по формулам:
· для сплошного вала круглого поперечного сечения (рис. 18.3, а)
· для полого вала круглого поперечного сечения (рис. 18.3, б)
· для шлицевого вала (рис. 18.3, в)
· для вала с одной призматической шпонкой (рис. 18.2, г)
где – диаметр опасного сечения вала (внутренний диаметр шлицевого вала), мм; dо – диаметр отверстия вала, мм; D – наружный диаметр шлицевого вала, мм; b – ширина шпонки (шлица), мм; h – высота шпонки, мм; z – число шлицев.
18.3. Поперечные сечения валов
Подставляя выражения (18.3) и (18.4) в условия прочности (18.2), получим формулу для проектного расчета вала:
где – эквивалентный момент, Н·мм.
Эквивалентный момент определяется по следующим выражениям:
Для тихоходных валов допускаемое напряжение определяется по формуле:
где – предел текучести материала вала, МПа; – коэффициент запаса прочности.
Для быстроходных валов допускаемое напряжение точнее определять по формуле:
где – предел выносливости материала при симметричном цикле изменения напряжений, МПа (см. табл. 18.1); – результирующий коэффициент, учитывающий влияние различных факторов на предел выносливости материала; – эффективный коэффициент концентрации напряжений; – коэффициент, учитывающий шероховатость поверхности; – коэффициент, учитывающий абсолютные размеры; – коэффициент долговечности.
Значения коэффициентов , и приведены в табл. 18.5 – 18.10.
Коэффициент долговечности определяется по формуле:
где – показатель степени кривой усталости; обычно или определяется из формулы ; для валов с прессовыми посадками ; – базовое число циклов перемен напряжений (при диаметре вала мм ; при диаметре вала > 50 мм ); – эквивалентное число циклов перемен напряжений (см. подразд. 9.7.1).
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать
Формулы для расчета эквивалентных напряжений
Эквивалентное напряжение по гипотезе максимальных касательных напряжений σэкв = √σ 2 + 4τ 2 .
Эквивалентное напряжение по гипотезе энергии формоизменения
где τ = MK / WP — расчетное касательное напряжение;
σ = M И / WX — расчетное нормальное напряжение.
Условие прочности при совместном действии изгиба
где Мэкв — эквивалентный момент.
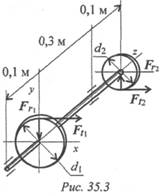
Эквивалентный момент по гипотезе максимальных касательных
напряжений Мэкв III = √М и² + М к².
Эквивалентный момент по гипотезе энергии формоизменения
Особенность расчета валов
Большинство валов испытывают сочетание деформаций изгиба и кручения. Обычно валы — прямые брусья с круглым или кольцевым сечением. При расчете валов касательные напряжения от действия поперечных сил не учитывают из-за их незначительности.
Тема 2.7. Расчет бруса круглого поперечного сечения 285
Расчеты проводят по опасным поперечным сечениям. При пространственном нагружении вала пользуются гипотезой независимости действия сил и изгибающие моменты рассматривают в двух взаимно перпендикулярных плоскостях, а суммарный изгибающий момент определяют геометрическим суммированием.
Примеры решения задач
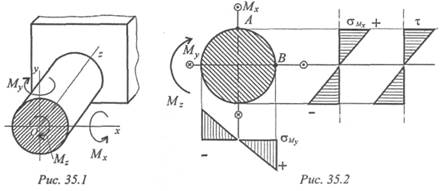
Пример 1. В опасном поперечном сечении круглого бруса возникают внутренние силовые факторы (рис. 35.1) Мх; Му; Mz .
Мх и Му — изгибающие моменты в плоскостях уОх и zOx соответственно; Mz — крутящий момент. Проверить прочность по гипотезе наибольших касательных напряжений, если [σ] = 120 МПа. Исходные данные: Мх = 0,9 кН∙м; Му = 0,8 кН•м; Mz = 2,2 кН • м; d = 60 мм.
Читайте также: Балансировка карданного вала украина
Строим эпюры нормальных напряжений от действия изгибающих моментов относительно осей Ох и Оу и эпюру касательных напряжений от кручения (рис. 35.2).
Максимальное касательное напряжение возникает на поверхности. Максимальные нормальные напряжения от момента Мх возникают в точке А, максимальные нормальные напряжения от момента Му в точке В. Нормальные напряжения складываются, потому что изгибающие моменты во взаимно перпендикулярных плоскостях геометрически суммируются.
Суммарный изгибающий момент: Ми = √М x² + М y²;
Рассчитываем эквивалентный момент по теории максимальных касательных напряжений:
Момент сопротивления сечения: Woceeoe = 0,1 • 60 3 = 21600 мм 3 .
Проверяем прочность:
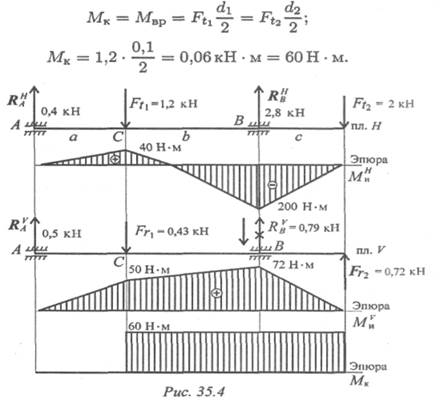
Пример 2. Из условия прочности рассчитать необходимый диаметр вала. На валу установлены два колеса. На колеса действуют две окружные силы F t 1 = 1,2 кН; Ft 2 = 2 кН и две радиальные силы в вертикальной плоскости Fr1 = 0,43 кН; Fr 2 = 0,72 кН (рис. 35.3). Диаметры колес соответственно равны d 1 = 0,1м; d2 = 0,06м.
Принять для материала вала [σ] = 50МПа.
Рассчитать размеры вала кольцевого сечения при с = 0,8 (с = dВН/ d). Расчет провести по гипотезе максимальных касательных напряжений. Весом вала и колес пренебречь.
Указание. Используем принцип независимости действия сил, составляем расчетные схемы вала в вертикальной и горизонтальной плоскостях. Определяем реакции в опорах в горизонтальной и вертикальной плоскостях в отдельности. Строим эпюры изгибающих моментов (рис. 35.4). Под действием окружных сил вал скручивается. Определяем действующий на валу крутящий момент.
Тема 2.7. Расчет бруса круглого поперечного сечения 287
Составим расчетную схему вала (рис. 35.4).
1. Крутящий момент на валу:
2. Изгиб рассматриваем в двух плоскостях : горизонтальной (пл. Н) и вертикальной (пл. V).
В горизонтальной плоскости определяем реакции в опоре:
Определяем изгибающие моменты в точках С и В:
Мс = 400 • 0,1 = 40Н • м; М В = -2000 • 0,1 = 200Н • м.
В вертикальной плоскости определяем реакции в опоре:
Определяем изгибающие моменты в точках С и В:
Суммарные изгибающие моменты в точках С и В:
В точке В максимальный изгибающий момент, здесь же действует и крутящий момент.
Расчет диаметра вала ведем по наиболее нагруженному сечению.
3. Эквивалентный момент в точке В по третьей теории
прочности
4. Определяем диаметр вала круглого поперечного сечения из
условия прочности
Округляем полученную величину: d — 36 мм.
Примечание. При выборе диаметров вала пользоваться стандартным рядом диаметров (Приложение 2).
5. Определяем необходимые размеры вала кольцевого сечения
при с = 0,8; с = — , где d — наружный диаметр вала.
Тема 2.7. Расчет бруса круглого поперечного сечения 289
Диаметр вала кольцевого сечения можно определить по формуле
Перегрузка незначительная. dBH = 0,8 d = 0,8 • 42 = 33,6 мм.
Округляем до значения dBH = 33 мм.
6. Сравним затраты металла по площадям сечения вала в обоих случаях.
Площадь поперечного сечения сплошного вала
Площадь поперечного сечения полого вала
Площадь поперечного сечения сплошного вала почти в два раза больше вала кольцевого сечения:
Контрольные вопросы и задания
1. Какое напряженное состояние возникает в поперечном сечении вала при совместном действии изгиба и кручения?
2. Напишите условие прочности для расчета вала.
3. Напишите формулы для расчета эквивалентного момента при расчете по гипотезе максимальных касательных напряжений и гипотезе энергии формоизменения.
4. Как выбирается опасное сечение при расчете вала?
Дата добавления: 2019-09-13 ; просмотров: 949 ; Мы поможем в написании вашей работы!
- Свежие записи
- Чем отличается двухтактный мотор от четырехтактного
- Сколько масла заливать в редуктор мотоблока
- Какие моторы бывают у стиральных машин
- Какие валы отсутствуют в двухвальной кпп
- Как снять стопорную шайбу с вала
- Правообладателям
- Политика конфиденциальности
Механика © 2023
Информация, опубликованная на сайте, носит исключительно ознакомительный характер📸 Видео
Что такое нормальное и касательное напряжение?Скачать
Сопромат. Напряжения. Доступным языком.Скачать
Реактивная мощность за 5 минут простыми словами. Четкий #энерголикбезСкачать
Основы Сопромата. НапряженияСкачать
Урок 12. Делитель напряжения на резисторахСкачать
Метод эквивалентных преобразований. Как находить токи и напряжения в цепиСкачать
Ременная передача. Урок №3Скачать
Часть 5. Гипотезы пластичности и разрушенияСкачать
как решать задачи со сложными схемамиСкачать
Метод эквивалентных преобразований │Найти общее сопротивление и токи в цепи │Задача #2Скачать
Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать
Детали машин. Лекция 4.1. Валы и оси.Скачать
9.1 Расчет валов приводаСкачать
Часть 1. Напряжения на наклонных площадкахСкачать
Кручение валаСкачать
ТЕХНИКА БЕЗОПАСНОСТИ. Вид Грубейшего Нарушения ТРЕБОВАНИЙ ТБ при работе на СТАНКАХ.Скачать
Расчет шнека, файлы Excel и RStudio | Расчёт и конструирование МАППСкачать
Метод эквивалентного генератораСкачать
