Эпюра крутящего момента схемы вала

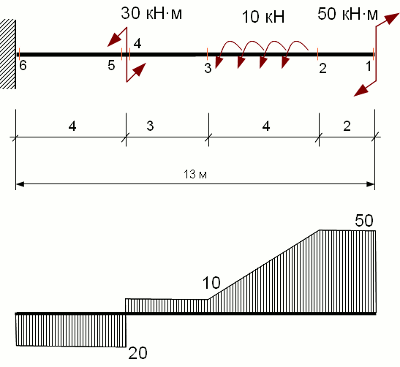
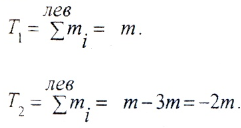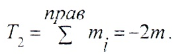Пусть прямолинейный стержень нагружен внешними сосредоточенными крутящими моментами Mкв1 = -30кН·м, Mкв2=50 кН·м, и распределенным моментом m1=10кН.

Реакции левой опоры можно не определять, т.к. в этом примере можно ограничиться рассмотрением лишь сил, приложенных к правым оставленным частям (справа от сечений).

Для заданного консольного стержня вычисления удобно вести, идя справа налево, начав их с 1–го сечения.

Проведем сечение 1. Определим крутящий момент в текущем сечении:

Проведем сечение 2. Отбросим левую часть, заменим ее действие крутящим моментом M к2 и составим уравнение равновесия в моментах относительно оси бруса. Из уравнения равновесия получаем выражение для крутящего момента в сечении 2:

M к2 = M к1 = M кв2 = 50 кНм

Проведем сечение 3, отбрасываем левую часть, составляем уравнение равновесия и получаем:

M к3 = M кв2 – m 1*4 = 50 – 10*4 = 10 кНм

Аналогично для сечения 4:

Также для сечения 5:

M к5= M к4-M кв1= 10 – 30 = -20 кНм

Для сечения 6:

По полученным значения строим эпюру крутящих моментов (см. рисунок).

Скачок на левом конце эпюры дает величину опорного момента (реактивного момента в заделке) M к6, так как реактивный момент – это внутреннее усилие, действующее в поперечном сечении, где соединены торец стержня и заделка.

Правила контроля правильности эпюр крутящих моментов

Для эпюр крутящих моментов характерны некоторые закономерности, знание которых позволяет оценить правильность построений.

• Эпюры крутящих моментов всегда прямолинейные.
• На участке, где нет распределенных моментов, эпюра M к – прямая, параллельная оси; а на участке с распределенными моментами – наклонная прямая.
• Под точкой приложения сосредоточенного момента на эпюре M к будет скачок на величину этого момента.

Видео:9.1 Расчет валов приводаСкачать

Построение эпюр крутящих моментов

Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов M_k (M_z) в поперечных сечениях по длине вала. Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.

В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣM_z=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 5.1, крутящий момент M_z в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M₁|=|M₂|.

В более сложных случаях, когда к валу приложено несколько внешних моментов, крутящие моменты M_k в поперечных сечениях различных участков вала неодинаковы.

На основании метода сечений крутящий момент в произвольном поперечном сечении вала численно равен алгебраической сумме внешних скручивающих моментов, приложенных к валу по одну сторону от рассматриваемого сечения.

При расчетах на прочность и жесткость знак крутящего момента не имеет никакого значения, но для удобства построения эп. M_k примем следующее правило знаков: крутящий момент считается положительным, если при взгляде в торец отсеченной части вала действующий на него момент представляется направленным по ходу часовой стрелки (рис.5.2).

В технике употребляется терминология « винт с правой нарезкой» или «…с левой нарезкой…», причем правый винт наиболее распространен, являясь стандартом. Полезно заметить, что при навинчивании гайки на правый винт мы прикладываем положительный момент M_кр , а при свинчивании гайки – отрицательный.

При наличии распределенной моментной нагрузки m (рис.5.3) крутящие моменты М_К связаны дифференциальной зависимостью

из которой вытекает следующая формула:

где – крутящий момент в начале участка.

Согласно формуле (5.2) на участках с равномерно распределенной нагрузкой m крутящий момент изменяется по линейному закону. При отсутствии погонной нагрузки (m = 0) крутящий момент сохраняет постоянное значение (М_К = М_Ко = const). В сечениях, где к валу приложены сосредоточенные скручивающие моменты, на эпюре М_К возникают скачки, направленные вверх, если моменты направлены против часовой стрелки, либо вниз – при обратном направлении моментов.

На рис. 5.4, а изображен стержень, жестко защемленный в правом концевом сечении, к которому приложены три внешних скручивающих момента.

В нашем случае крутящие моменты в их поперечных сечениях удобно выражать через внешние моменты, приложенные со стороны свободного конца бруса.

Это позволяет определять крутящие моменты, не вычисляя реактивного момента, возникающего в заделке.

Крутящий момент M_z1 в сечении I численно равен M₁=200 нм и, согласно принятому правилу знаков, положителен.

Крутящий момент M_z2 в сечении II численно равен алгебраической сумме моментов M₁ и M₁, т.е. M_z2 =200-300=-100 нм, а его знак зависит от соотношения этих моментов.

Аналогичным образом вычисляется крутящий момент M_z3 в сечении III: M_z3 =200-300+500=400 нм.

Изменение крутящих моментов по длине вала покажем с помощью эпюры крутящих моментов. На рис. 5.4, б показана такая эпюра для стержня, изображенного на рис. 5.4, а.

Каждая ордината эп. M_k в принятом масштабе равна величине крутящего момента, действующего в том поперечном сечении бруса, которому соответствует эта ордината.

В сечении, в котором к брусу приложен внешний скручивающий момент, ордината эпюры изменяется скачкообразно на величину, равную значению этого момента.

Следует учитывать, что наибольший внешний скручивающий момент, приложенный к брусу, не всегда равен наибольшему крутящему моменту, по которому ведется расчет бруса на прочность и жесткость.

Построить эпюру крутящих моментов для жестко защемленного стержня (рис.5.4.1, а).

Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил.

1. Намечаем характерные сечения.

2. Определяем крутящий момент в каждом характерном сечении.

3. По найденным значениям строим эпюру (рис.5.4.1, б).

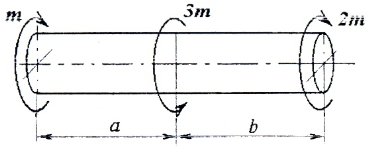
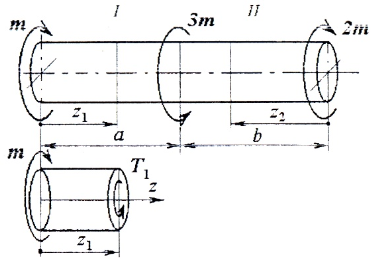
Рассмотрим расчетную схему ва­ла, нагруженного двумя сосредоточенными моментами М и 2М и распределенными по длине: т (рис. 5.4.2).

Читайте также: Компрессор кондиционера фольксваген поло седан 2011 года

Рис. 5.4.2. Построение эпюры внутренних крутящих моментов:

а – расчетная схема; б – первый участок, левая часть; в – второй участок, левая часть;

г – третий участок, правая часть; д – эпюра внутренних крутящих моментов

В исходных сечениях 1–1; 2–2; 3–3 задаются положительными зна­чениями внутренних крутящих мо­ментов М₁, М₂, М₃. Пусть .

Для первого участка (рис. 5.4.2, б):

Для второго участка (рис. 5.4.2, в):

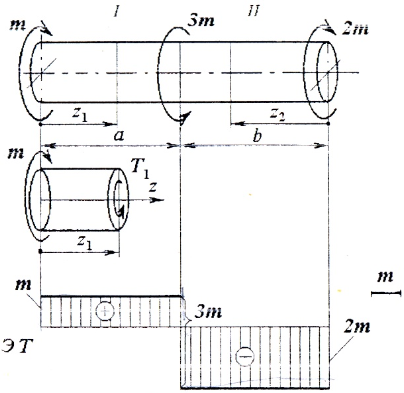
Для третьего участка (рис. 5.4.2, г):

Границы измерения параметра х₃ в следующей системе координат:

Отмеченные значения ординат откладываются на эпюре внутренних крутящих моментов (рис. 5.4.2, д).

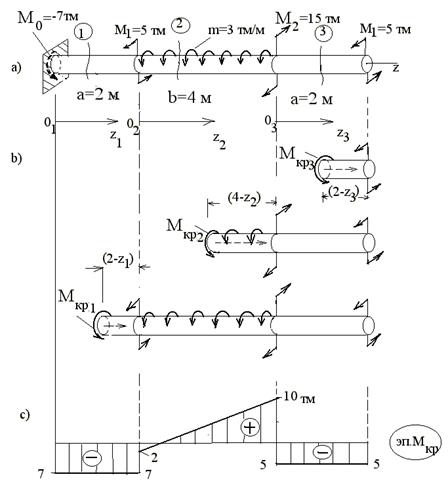
На рис. 5.4.3 дан пример определения по методу сечений внутренних крутящих моментов по участкам и внизу (ри.5.4.3, с) изображена суммарная эпюра М_кр.

Рис.5.4.3. a) заданный стержень с нагрузкой; b) отсеченные части стержня;

с) эпюра крутящих моментов.

В данном случае для консольного стержня вести вычисления удобно, идя справа налево, начав их с 3–го участка.

Участок 3(рис. 5.4.3, b). Неизвестный момент M_кр3 прикладываем к отсеченной части как положительный, после чего пишем условие равновесия отсеченной части:

Участок 2(рис. 5.4.3, b). Положение сечения фиксируем с помощью местной координаты z₂ :

Участок 1(рис. 5.4.3, b):

Найдем реактивный момент в заделке M₀ из условия равновесия всего стержня Σm_z =0, это дает M₀ +3∙4+5+5-15=0 и M₀ = -7 тм, что совпадает с M_кр1 , найденным на участке 1 по методу сечений. Этого конечно следовало ожидать, так как по существу реактивный момент – это внутреннее усилие, действующее в поперечном сечении, где соединены торец стержня и заделка.

Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычис­лить, когда этот.

ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между.

Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право.

ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования.

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать

iSopromat.ru

Пример решения задачи на построение эпюры скручивающих моментов при кручении вала по силовым участкам методом сечений.

Задача
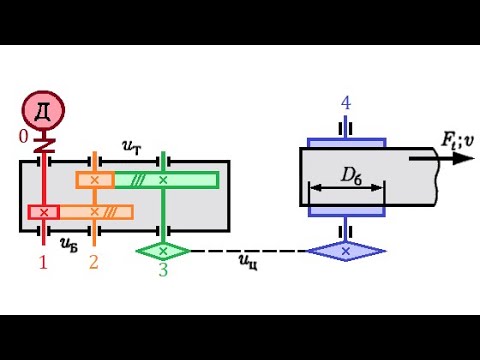
Построить эпюру крутящих моментов для следующей расчетной схемы вала:

На рассматриваемом валу можно выделить два силовых участка.

Границами участков являются сечения, в которых приложены скручивающие моменты.

Используя метод сечений и правило знаков при кручении, определяем величины крутящих моментов на I и II участках:


Следует отметить, что значения крутящего момента не зависят от того, правую или левую от проведенного сечения часть вала мы рассматриваем.

Например, для второго участка, рассматривая правую от сечения часть вала, получим:

По полученным значениям строится эпюра крутящих моментов:

Если к валу приложены только сосредоточенные скручивающие моменты, эпюра крутящего момента в пределах каждого участка вычерчивается прямыми, параллельными базовой линии.

В тех сечениях, где к валу приложены крутящие моменты m_i, на эпюре T имеют место скачки, по модулю равные величине моментов m_i.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

ПроСопромат.ру

Видео:6.2 Кинематический расчет приводаСкачать

Технический портал, посвященный Сопромату и истории его создания

Видео:ПЗ Часть 1 Построение эпюры крутящего моментаСкачать

Архив рубрики: Задачи на кручение

Видео:ПЗ Часть 3 Эпюра крутящего моментаСкачать

Проверочный и проектный расчеты при кручении

Задача. Для заданного стального бруса d=50мм (материал – сталь Ст3) построить эпюры крутящих моментов, углов поворота поперечных сечений. Проверить прочность бруса, если допускаемое касательное напряжение [τ]=30МПа. Подобрать для бруса кольцевое сечение при . Сравнить сечения по расходу материала.

1.Расставляем сечения на характерных участках. Начинаем расчет от свободного конца бруса, рассматривая правую часть и отбрасывая оставшуюся левую часть с заделкой. Каждое сечение рассматриваем отдельно, определяя в нем значение крутящего момента.

Строим эпюру М_К

2.Строим эпюру углов поворота сечений. Углы поворота сечений определяем по формуле

Расчет ведем по сечениям от неподвижного конца – стены А, в которой угол поворота равен нулю φ_А=0. В формуле обязательно следует учитывать знаки крутящих моментов.

Модуль сдвига для Ст3 G = 0,8·10 5 МПа = 0,8·10 8 кПа.

Определим полярный момент инерции для круглого сечения:

Вычисляем углы поворота сечений — от стены А.

Если требуется перейти к градусной мере, то:

Далее вычисляем все последующие углы поворота, учитывая ранее найденные:

Строим эпюру φ

3.Проверим прочность бруса по формуле

Максимальный крутящий момент с эпюры М_К = 0,75 кНм.

Определим полярный момент сопротивления сечения:

Тогда —прочность обеспечена.

4.Подбираем кольцевое сечение для вала с .

Наружный диаметр кольца определим по формуле проектного расчета для кольцевого сечения:

Тогда d = 0,8 · 60 = 48 мм.

Проверим прочность подобранного сечения. Полярный момент сопротивления для кольца:

5. Сравним варианты – круглое и кольцевое – по расходу материала

В задаче площадь круглого вала А = 19,6 см 2 , а у кольцевого сечения (полого) А = 10,7 см 2 , что позволяет говорить об экономии материала почти в два раза. Т.о. брус (вал) кольцевого сечения экономичнее равнопрочного сплошного.

Видео:Прочность и жесткость валов. Часть 6: Эпюры моментов выходного вала (цилиндрическая передача).Скачать

Задача на кручение

Для вала определить диаметр, построить эпюры крутящих моментов и углов закручивания.

1) Определяем величины внутренних крутящих моментов M. Для этого разбиваем стержень на участки (I, II, III, IV) и производим расчёт M со свободного конца стержня. Крутящий момент M в сечении равен алгебраической сумме моментов, действующих на стержень с одной стороны (справа) от рассматриваемого сечения.

Читайте также: Допуск при центровке валов

Расчёт M соответственно по участкам IV, III, II, I:

Зная числовые значения крутящих моментов M, строится эпюра M, при этом положительные значения M откладываются вверх, а отрицательные – вниз от горизонтальной линии.

2) Определяем диаметр стержня из условия прочности: Выразим –полярный момент сопротивления при кручении круглого стержня через диаметр:тогда получим:

берётся из эпюры M по абсолютному значению. Диаметр стержня d округляется до большей величины.

3) Производим расчет жесткости вала при кручении, где — модуль сдвига, а (см 4 ) – полярный момент инерции сечения.

4) Производим расчет – углов закручивания концов участков стержня, начиная от закреплённого конца стержня, где ,(рад):Значения крутящих моментов на участках берутся из эпюры крутящих моментов с учётом их знака. Получив численные значения , строят эпюру . Примерная эпюра показана на рисунке.

Видео:БАЛКА - 90 СТУДЕНТОВ САМОСТОЯТЕЛЬНО СТРОЯТ ЭПЮРЫ после просмотра этого видео!Скачать

Задача

Ступенчатый стержень нагружен крутящим моментом Т .При каком отношении выполняется условие одинаковой прочности по всей длине стержня, если

Условие одинаковой прочности на участках будет выполнено в том случае ,если касательные напряжения будут одинаковы.

Определим касательные напряжения, обозначив крутящий момент в левой стене как , а в правой как :

Определим полярные моменты сопротивления сечений : Тогда найдем соотношение между и :

Теперь составим уравнение деформаций — углов поворота. Начнем от правой стены В, в которой . Внутренний крутящий момент во втором сечении будет равен , а крутящий момент в первом сечении будет равен . Тогда уравнение углов поворота: (2)

Полярные моменты инерции: Подставим эти значения в уравнение (2) и найдем соотношение между и :

Составим уравнение статики для заданной схемы:Тогда: (4)

Теперь, решая (4) , (3) и (1), получим отношение . Задача решена.

Видео:КРУЧЕНИЕ. ЭПЮРЫ ЗАКРУЧИВАНИЯ. Углы поворота. СопроматСкачать

Задача на расчет вала на прочность и жесткость при кручении

Для стального вала, нагруженного внешними крутящими моментами, построить эпюры внутренних крутящих моментов, определить размеры поперечного сечения в виде кольца (d/D=0,85) из условий прочности и жесткости, построить эпюры максимальных касательных напряжений, абсолютных и относительных углов поворота поперечных сечений.

Определим внутренние крутящие моменты. Расчет внутренних крутящих моментов проводится с помощью метода сечений.

Участок LK: М_L= М₄ = 5 кНм; М_К=М₄=5кНм.

Покажем эпюру крутящих моментов на рис.б.

Определяем размеры поперечного сечения вала из условия прочности и жесткости:, где полярный момент сопротивления сечения и полярный момент инерции сечения равны:Максимальный внутренний крутящий момент:

Тогда из условия прочности:

А из условия жесткости: Окончательно принимаем D=90мм.

Для подобранного сечения вала его геометрические характеристики:

Рассчитаем касательные напряжения для участков:

Построим эпюру касательных напряжений на рис.в.

Расчет относительных углов поворота на участках:

Сначала определим жесткость сечения вала при кручении:

Эпюра θ показана на рис. г.

Определение угловых перемещений характерных сечений (идем от опоры В, в которой угол поворота равен 0):

Эпюра φ представлена на рис.д.

Видео:Структурный анализ, поэтажная схема, эпюры моментов и сил много пролетной балкиСкачать

Задача на температурные напряжения при кручении

Стальные стержни 1 и 2 нагреваются на . Площадь стержней А.

Определить максимальные напряжения.

При нагреве стержней на возникнут температурные напряжения.

Напряжения, вызванные изменением температуры в стержне постоянного сечения, не зависят от его длины, площади поперечного сечения, а зависят от модуля упругости, коэффициента линейного расширения и разности температур .

Эти напряжения создадут усилия:

Тогда крутящий момент:

Касательные напряжения:

Следует помнить, что при нагреве стержней в них возникают сжимающие напряжения, а при охлаждении – растягивающие. Эти напряжения, суммируясь с напряжениями от силовых факторов, могут значительно превышать допускаемые. Это обстоятельство следует учитывать при проектировании элементов конструкций.

Видео:Построение эпюры крутящих моментовСкачать

Задача

К стальному валу приложены три известных момента:

Требуется: 1) установить, при каком значении Х угол поворота правого крайнего сечения вала равен нулю; 2) для найденного значения Х построить эпюру крутящих моментов; 3) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его до ближайшей большей величины, соответственно равной 30, 35, 40, 45, 50, 60, 70, 80, 90, 100 мм; 4) построить эпюру углов поворота; 5) найти наибольший относительный угол закручивания (в градусах на 1м длины).

Решение: Обозначим границы участков русскими буквами А,……,Д.

I.Записываем условие, что угол поворота крайнего правого сечения (Д) вала равен нулю – исходя из условий задачи.

Данный угол поворота является суммой углов поворота вала на каждом участке:

Угол поворота на участке определяется по формуле:

, где М к — крутящий момент на данном участке, l — длина участка,

G — модуль сдвига , — для стали

— полярный момент инерции

Таким образом, , и с учетом условия задачи:

Так как вал имеет постоянное поперечное сечение, то

Определяем внутренние крутящие моменты на участках методом сечений. Идем от свободного конца вала, на каждом участке мысленно проводим сечение и рассматриваем равновесие всегда правой отсеченной части:

Подставляем найденные значения моментов в уравнение (1) :

2. Строим эпюру крутящих моментов. Для этого подставляем в выражения для моментов Мк найденные значения Х.

Полученные значения откладываем в виде ординат на эпюре

3.Определяем диаметр вала из условия прочности:

, где —максимальное касательное напряжение,

— максимальный крутящий момент (берется с эпюры Мкр по модулю),

— полярный момент сопротивления сечения

[τ]=80 МПа — допускаемое касательное напряжение

Определяем диаметр:

Принимаем диаметр вала d=45 мм=4,5 см

4. Построение эпюры углов поворота начинаем от опоры и строим нарастающим итогом. Предварительно посчитаем жесткость вала:

Угол поворота в левой опоре равен нулю, поскольку в заделке поворота быть не может:

Читайте также: Как снять внутреннюю обойму подшипника с вала без съемника ступицы

В последней точке угол поворота должен получиться равным нулю (по условию задачи), таким он и получился. Строим эпюру углов поворота.

5. Наибольший относительный угол закручивания определим по формуле:

Полученный результат переведем в градусы на метр длины:

Видео:11. Кручение ( практический курс по сопромату )Скачать

Статически неопределимые задачи при кручении. Задача2

Требуется: 1) Построить эпюру крутящих моментов и подобрать размеры поперечных сечений заданной формы, соблюдая следующие соотношения между ними:

2) Построить эпюру углов поворота.

Сначала составляем уравнение статики для всего бруса:

Здесь два неизвестных, следовательно, требуется еще одно уравнение. Его получим, если сформулируем условие совместности деформаций всех трех участков бруса. Оно заключается в том, что поворот правого опорного сечения относительно левого опорного сечения для рассматриваемого бруса невозможен, поскольку оба его концы жестко защемлены:

Сократим на , тогда будет:

Выразим моменты инерции сечений разных форм с учетом заданных соотношений размеров:

Итак, все моменты инерции выражены через один параметр с, что позволит довести до числа решение уравнения (2′):

или после сокращения на с 4 :

С помощью метода сечений выразим неизвестные крутящие моменты через один из реактивных опорных моментов, например, через М_А:

С учетом (а), (б) и (в) уравнение (2′′), будет:

откуда находим значение М_А:

Тогда из (а), (б) и (в) найдем:

Эти результаты показаны в виде эпюры крутящих моментов.

Подбор размеров сечений производится по условиям прочности:

— на первом участке

Для круглого сечения

При заданном соотношении d=c:

— на втором участке

Для кольцевого сечения

Здесь мы должны учесть соотношения размеров, при которых и найдены внутренние усилия, то – есть

— на третьем участке

Для прямоугольного сечения . При соотношениях

По таблице α=0,246. И тогда W_к=2∙0,246∙с 3 .

Из условия прочности

Из трех требуемых значений «с» (0,023м, 0,04м и 0,046м) принимаем наибольшее с=0,046м и тогда проектные значения размеров сечений на разных участках должны быть

— на первом участке: круглое сечение диаметром d=0,046м,

— на втором участке: кольцевое сечение с внутренним диаметром d=0,046м, а внешним у которого

— на третьем участке: прямоугольное сечение шириной b=c=0,046м

и высотой h=2b=2∙0,046=0,092 м,

у которого I_к=β∙h∙b 3 =0,229∙0,092∙0,046 3 =205∙10 -8 м 4 .

2. Построение эпюры углов поворота.

Для этого вычисляются углы поворота сечений, расположенных на границах участков бруса (эти сечения на схеме обозначены цифрами в кружочках), они откладываются в виде ординат, вершины которых соединяются прямыми линиями. Так:

α₀=0, поскольку крайнее левое сечение жестко защемлено и поворачиваться вокруг продольной оси z не может,

Равенство нулю угла поворота крайнего правого сечения, тоже жестко защемленного, служит контролем правильности всего решения задачи.

Видео:Сопромат. Практическое занятие №1.4Скачать

Статически неопределимые задачи при кручении. Задача1

Уравнение статики для всего бруса:

В этом уравнении два неизвестных (это реактивные моменты в опорах М_А и М_В). Следовательно, задача один раз статически неопределима, и для ее решения необходимо составить дополнительное уравнение, выражающее факт совместности деформаций всех участков бруса.

Здесь можно рассуждать следующим образом: если удалить одну из опор, то брус станет статически определимым

Теперь крайнее правое сечение получило возможность поворачиваться. Но в заданной системе этот поворот невозможен. Поэтому величину М_В в удаленной опоре следует подобрать так, чтобы угол поворота опорного сечения равнялся нулю:

α_В=0 – это условие деформации.

Раскрывая его, будем иметь:

Тогда условие совместности деформаций (а) превращается в уравнение совместности деформаций:

В этом уравнении три неизвестных крутящих момента (по количеству участков бруса). Для их определения выразим крутящие моменты через заданные внешние скручивающие моменты М₁, М₂ и реактивные моменты, используя метод сечений. Так в любом сечении первого участка:

((b)

Далее, в любом сечении второго участка

Наконец, в любом сечении третьего участка:

Подставляя (b), © и (d) в уравнение (2), будем иметь:

В этом уравнении содержится одно-единственное неизвестное: это реактивный момент в левой опоре М_А. Определив его из решения уравнения (2′), обратной подстановкой в формулы (b), © и (d) определим численные значения крутящих моментов , Таким образом статическая неопределимость задачи будет раскрыта.

Зная крутящие моменты, далее можно решить любую задачу прочности и жесткости бруса.

Видео:Правило знаков при крученииСкачать

Кручение бруса тонкостенного замкнутого круглого сечения

Тонкостенное круглое сечение характеризуется средним радиусом R_ср и толщиной стенки трубы δ

Считается, что касательные напряжения по толщине стенки распределяются равномерно и равны:

Угол закручивания

Видео:9.4. Расчет валов и осейСкачать

Кручение бруса прямоугольного сечения

Опыт показывает, что при кручении брусьев некруглого поперечного сечения сами сечения не остаются плоскими, то есть происходит депланация поперечных сечений. Исследовать напряженное и деформированное состояние таких брусьев при кручении методами сопротивления материалов не представляется возможным, так как в основе их лежит гипотеза плоских сечений (гипотеза Бернулли).

Задача о кручении бруса некруглого, в частности, прямоугольного сечения решена с помощью метода теории упругости, и на основе этого решения предложены простые расчетные формулы, имеющие ту же структуру, что и формулы для бруса круглого сечения, а именно:

Здесь: W_к=α∙h∙b 2 – момент сопротивления при кручении,

В этих формулах: b – меньшая из сторон прямоугольника,

h – большая сторона,

α, β – коэффициенты, значения которых приводятся в таблице в зависимости от отношения сторон h/b (эта таблица содержится в рубрике «Кручение», «Таблицы» или в любом учебнике сопротивления материалов).

Распределение касательных напряжений по прямоугольному сечению тоже отличается от распределения в круглом сечении:

Значения коэффициента γ Запись опубликована 05.09.2014 автором admin в рубрике Задачи, Задачи на кручение.

• Свежие записи
  • Чем отличается двухтактный мотор от четырехтактного
  • Сколько масла заливать в редуктор мотоблока
  • Какие моторы бывают у стиральных машин
  • Какие валы отсутствуют в двухвальной кпп
  • Как снять стопорную шайбу с вала

  
  

  источники:

  https://evakuatorinfo.ru/epyura-krutyaschego-momenta-shemy-vala

  📽️ Видео

  Расчетная схема ведомого валаСкачать

  

  Кручение. Часть 1 Общие сведенияСкачать

  

  Понимание напряжений в балкахСкачать

  

  Изгиб с кручениемСкачать