Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов Mk (Mz) в поперечных сечениях по длине вала. Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.
В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣMz=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 5.1, крутящий момент Mz в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M1|=|M2|.
В более сложных случаях, когда к валу приложено несколько внешних моментов, крутящие моменты Mk в поперечных сечениях различных участков вала неодинаковы.
На основании метода сечений крутящий момент в произвольном поперечном сечении вала численно равен алгебраической сумме внешних скручивающих моментов, приложенных к валу по одну сторону от рассматриваемого сечения.
При расчетах на прочность и жесткость знак крутящего момента не имеет никакого значения, но для удобства построения эп. Mk примем следующее правило знаков: крутящий момент считается положительным, если при взгляде в торец отсеченной части вала действующий на него момент представляется направленным по ходу часовой стрелки (рис.5.2).
В технике употребляется терминология « винт с правой нарезкой» или «…с левой нарезкой…», причем правый винт наиболее распространен, являясь стандартом. Полезно заметить, что при навинчивании гайки на правый винт мы прикладываем положительный момент Mкр , а при свинчивании гайки – отрицательный.
При наличии распределенной моментной нагрузки m (рис.5.3) крутящие моменты МК связаны дифференциальной зависимостью
из которой вытекает следующая формула:
где – крутящий момент в начале участка.
Согласно формуле (5.2) на участках с равномерно распределенной нагрузкой m крутящий момент изменяется по линейному закону. При отсутствии погонной нагрузки (m = 0) крутящий момент сохраняет постоянное значение (МК = МКо = const). В сечениях, где к валу приложены сосредоточенные скручивающие моменты, на эпюре МК возникают скачки, направленные вверх, если моменты направлены против часовой стрелки, либо вниз – при обратном направлении моментов.
На рис. 5.4, а изображен стержень, жестко защемленный в правом концевом сечении, к которому приложены три внешних скручивающих момента.
В нашем случае крутящие моменты в их поперечных сечениях удобно выражать через внешние моменты, приложенные со стороны свободного конца бруса.
Это позволяет определять крутящие моменты, не вычисляя реактивного момента, возникающего в заделке.
Видео:КРУЧЕНИЕ. ЭПЮРЫ ЗАКРУЧИВАНИЯ. Углы поворота. СопроматСкачать
Крутящий момент Mz1 в сечении I численно равен M1=200 нм и, согласно принятому правилу знаков, положителен.
Крутящий момент Mz2 в сечении II численно равен алгебраической сумме моментов M1 и M1, т.е. Mz2 =200-300=-100 нм, а его знак зависит от соотношения этих моментов.
Аналогичным образом вычисляется крутящий момент Mz3 в сечении III: Mz3 =200-300+500=400 нм.
Изменение крутящих моментов по длине вала покажем с помощью эпюры крутящих моментов. На рис. 5.4, б показана такая эпюра для стержня, изображенного на рис. 5.4, а.
Читайте также: Датчик положения коленчатого вала нексия f16d3
Каждая ордината эп. Mk в принятом масштабе равна величине крутящего момента, действующего в том поперечном сечении бруса, которому соответствует эта ордината.
В сечении, в котором к брусу приложен внешний скручивающий момент, ордината эпюры изменяется скачкообразно на величину, равную значению этого момента.
Следует учитывать, что наибольший внешний скручивающий момент, приложенный к брусу, не всегда равен наибольшему крутящему моменту, по которому ведется расчет бруса на прочность и жесткость.
Построить эпюру крутящих моментов для жестко защемленного стержня (рис.5.4.1, а).
Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил.
1. Намечаем характерные сечения.
2. Определяем крутящий момент в каждом характерном сечении.
3. По найденным значениям строим эпюру (рис.5.4.1, б).
Рассмотрим расчетную схему вала, нагруженного двумя сосредоточенными моментами М и 2М и распределенными по длине: т (рис. 5.4.2).
Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать
Рис. 5.4.2. Построение эпюры внутренних крутящих моментов:
а – расчетная схема; б – первый участок, левая часть; в – второй участок, левая часть;
г – третий участок, правая часть; д – эпюра внутренних крутящих моментов
В исходных сечениях 1–1; 2–2; 3–3 задаются положительными значениями внутренних крутящих моментов М1, М2, М3. Пусть .
Для первого участка (рис. 5.4.2, б):
Для второго участка (рис. 5.4.2, в):
Для третьего участка (рис. 5.4.2, г):
Границы измерения параметра х3 в следующей системе координат:
Отмеченные значения ординат откладываются на эпюре внутренних крутящих моментов (рис. 5.4.2, д).
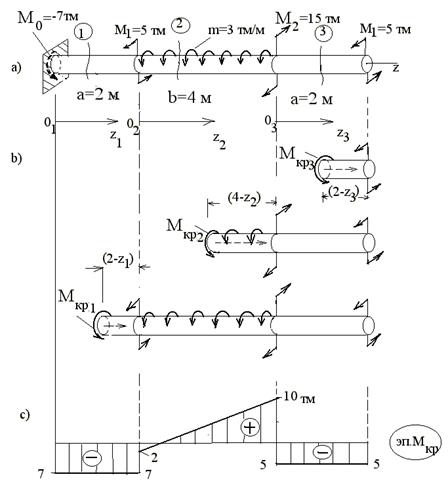
На рис. 5.4.3 дан пример определения по методу сечений внутренних крутящих моментов по участкам и внизу (ри.5.4.3, с) изображена суммарная эпюра Мкр.
Рис.5.4.3. a) заданный стержень с нагрузкой; b) отсеченные части стержня;
с) эпюра крутящих моментов.
Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать
В данном случае для консольного стержня вести вычисления удобно, идя справа налево, начав их с 3–го участка.
Участок 3(рис. 5.4.3, b). Неизвестный момент Mкр3 прикладываем к отсеченной части как положительный, после чего пишем условие равновесия отсеченной части:
Участок 2(рис. 5.4.3, b). Положение сечения фиксируем с помощью местной координаты z2 :
Участок 1(рис. 5.4.3, b):
Найдем реактивный момент в заделке M0 из условия равновесия всего стержня Σmz =0, это дает M0 +3∙4+5+5-15=0 и M0 = -7 тм, что совпадает с Mкр1 , найденным на участке 1 по методу сечений. Этого конечно следовало ожидать, так как по существу реактивный момент – это внутреннее усилие, действующее в поперечном сечении, где соединены торец стержня и заделка.
ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между.
ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала.
Читайте также: Сальник первичного вала кпп kia ceed 2013
Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем.
Видео:Задача 3. Часть 1. - Построение эпюр моментов для пространственной рамыСкачать
Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Построение эпюры крутящих моментов
Крутящий момент возникает как при действии пары сил, приложенной в плоскости поперечного сечения, так и при действии одной силы, приложенной с эксцентриситетом по отношению к центру тяжести поперечного сечения. В первом случае сумма всех сил, действующих относительно оси х и относительно оси у равна 0 и для расчетов из 4 возможных уравнений равновесия используется только одно — уравнение крутящих моментов.
При действии крутящего момента, вызванного действием одной силы, для расчетов используются все 4 возможных уравнения равновесия. При этом уравнение крутящих моментов в плоскости поперечного сечения остается неизменным. Особенности использования первых 3 уравнений равновесия рассматриваются отдельно. Здесь же мы рассмотрим только использование уравнения крутящих моментов в плоскости поперечных сечений:
∑Мk = 0 (333.1)
При действии крутящего момента стержни, исходя из условий равновесия, могут иметь одну или две жестко защемленные опоры. Опоры могут быть также скользящими, при этом поворот стержней в плоскости действия крутящего момента невозможен. Шарнирное опирание стержней при действии крутящего момента не рассматривается. Т.е. стержни могут иметь шарнирные опоры в плоскости действия изгибающего момента, но при этом они должны иметь жестко защемленные опоры в плоскости действия крутящего момента.
Таким образом, если стержень имеет только одну жестко защемленную опору, то такая конструкция является статически определимой, при этом опорный крутящий момент равен по значению крутящему моменту, действующему в пролете и противоположен по знаку. Если на рассматриваемый стержень действует только один сосредоточенный крутящий момент, приложенный в некоторой точке С, то уравнение равновесия будет выглядеть так:
Если стержень имеет две жестко защемленные опоры, то конструкция является один раз статически неопределимой, в таких случаях уравнения моментов в плоскости поперечного сечения для определения опорных моментов:
недостаточно и для расчетов используется дополнительное уравнение. Это уравнение можно получить, исходя из условия совместимости деформаций:
Смысл этого уравнения в том, что крутящий момент на опоре А приводит к повороту сечения, в плоскости которого действует сосредоточенный изгибающий момент (в точке С), на такой же угол, как и крутящий момент на опоре В. Тогда согласно формулы
Например, при действии сосредоточенного крутящего момента MkC = 12 кгс·см, приложенного на расстоянии 1 м от опоры А (l1 = 1 м) при длине вала l = 3 м (l2 = 2м) совместное решение уравнений (333.4) и (333.2.2) даст следующий результат: МkA = — 8 кгс·см, MkB = — 4 кгс·см. В данном случае знаки «-» означают, что опорные моменты направлены в сторону, противоположную для крутящего момента в точке С. При этом эпюра крутящих моментов и эпюра углов поворота будут выглядеть так:
Читайте также: Подшипник первичного вала foton 1069
Видео:11. Кручение ( практический курс по сопромату )Скачать
Рисунок 333.1
Если внимательно посмотреть на эти эпюры, то мы заметим, что эпюра крутящих моментов при воздействии сосредоточенного момента подобна эпюре поперечных сил при воздействии сосредоточенной нагрузки на стержень, имеющий шарнирные опоры, а эпюра углов поворота подобна эпюре изгибающих моментов. Кроме того, опорные реакции при воздействии сосредоточенной нагрузки имеют такую же зависимость, как и опорные моменты при воздействии сосредоточенного крутящего момента. А уравнение равновесия относительно оси у подобно уравнению крутящих моментов.
На основании этого можно предположить, что при воздействии равномерно распределенного крутящего момента эпюра крутящего момента будет подобна эпюре поперечных сил для стержня на шарнирных опорах, на который действует равномерно распределенная нагрузка. А эпюра углов поворота в плоскости поперечных сечений будет подобна эпюре моментов:
Рисунок 333.2
Такое же подобие можно установить и для других возможных видов загружения стержней.
Для стержней круглого сечения — валов машин и механизмов, на которые действует крутящий момент от пары сил, этих данных достаточно для расчета. При расчете строительных конструкций, на которые действует крутящий момент от нагрузки приложенной со смещением от центра тяжести поперечных сечений, необходимо учитывать совместную работу изгибающего и крутящего моментов. При этом определение максимально допустимых напряжений производится согласно одной из теорий прочности. И если для стержней с шарнирными опорами при равномерно распределенном крутящем моменте как правило достаточно исследовать плоское напряженное состояние в виду того, что изгибающий момент на шарнирных опорах отсутствует, то для стержней с жестко защемленными опорами как в плоскости действия изгибающего момента, так и в плоскости действия крутящего момента следует исследовать объемное напряженное состояние, так как возле опор напряжения будут направлены в 3 плоскостях.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).
- Свежие записи
- Чем отличается двухтактный мотор от четырехтактного
- Сколько масла заливать в редуктор мотоблока
- Какие моторы бывают у стиральных машин
- Какие валы отсутствуют в двухвальной кпп
- Как снять стопорную шайбу с вала
источники:Видео:Построение эпюры крутящих моментовСкачать
https://evakuatorinfo.ru/epyura-krutyaschih-momentov-dlya-ne-zaschemlennogo-vala
🎦 Видео
Кручение валаСкачать
БАЛКА - 90 СТУДЕНТОВ САМОСТОЯТЕЛЬНО СТРОЯТ ЭПЮРЫ после просмотра этого видео!Скачать
28. Статически неопределимый стержень ( кручение ) ( практический курс по сопромату )Скачать
Вот для чего нужно строить эпюры в сопромате!Скачать
Определение реакций опор в балке. Сопромат.Скачать
РАСТЯЖЕНИЕ-СЖАТИЕ. Построение эпюр. Сопромат.Скачать
Определение усилий, напряжений и перемещений. СопроматСкачать
4. Построение эпюр в раме ( практический курс по сопромату )Скачать
РАМА. ПОСТРОЕНИЕ ЭПЮР Q, M, N. Сопромат.Скачать
Сопромат. Часть 1. Растяжение (сжатие). Построение эпюр продольных сил и нормальных напряжений.Скачать
Кручение круглого стержняСкачать
Балка. Реакции в заделке. Реакции опор. Сопромат.Скачать
Понимание напряжений в балкахСкачать
Основы сопромата. Задача 5. Расчет стержня на кручениеСкачать
