Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов Mk (Mz) в поперечных сечениях по длине вала. Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.
В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣMz=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 5.1, крутящий момент Mz в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M1|=|M2|.
В более сложных случаях, когда к валу приложено несколько внешних моментов, крутящие моменты Mk в поперечных сечениях различных участков вала неодинаковы.
На основании метода сечений крутящий момент в произвольном поперечном сечении вала численно равен алгебраической сумме внешних скручивающих моментов, приложенных к валу по одну сторону от рассматриваемого сечения.
При расчетах на прочность и жесткость знак крутящего момента не имеет никакого значения, но для удобства построения эп. Mk примем следующее правило знаков: крутящий момент считается положительным, если при взгляде в торец отсеченной части вала действующий на него момент представляется направленным по ходу часовой стрелки (рис.5.2).
В технике употребляется терминология « винт с правой нарезкой» или «…с левой нарезкой…», причем правый винт наиболее распространен, являясь стандартом. Полезно заметить, что при навинчивании гайки на правый винт мы прикладываем положительный момент Mкр , а при свинчивании гайки – отрицательный.
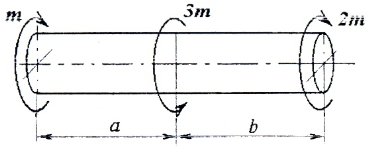
При наличии распределенной моментной нагрузки m (рис.5.3) крутящие моменты МК связаны дифференциальной зависимостью
из которой вытекает следующая формула:
где – крутящий момент в начале участка.
Согласно формуле (5.2) на участках с равномерно распределенной нагрузкой m крутящий момент изменяется по линейному закону. При отсутствии погонной нагрузки (m = 0) крутящий момент сохраняет постоянное значение (МК = МКо = const). В сечениях, где к валу приложены сосредоточенные скручивающие моменты, на эпюре МК возникают скачки, направленные вверх, если моменты направлены против часовой стрелки, либо вниз – при обратном направлении моментов.
На рис. 5.4, а изображен стержень, жестко защемленный в правом концевом сечении, к которому приложены три внешних скручивающих момента.
В нашем случае крутящие моменты в их поперечных сечениях удобно выражать через внешние моменты, приложенные со стороны свободного конца бруса.
Это позволяет определять крутящие моменты, не вычисляя реактивного момента, возникающего в заделке.
Крутящий момент Mz1 в сечении I численно равен M1=200 нм и, согласно принятому правилу знаков, положителен.
Читайте также: Длина вала привода для ваз 2108
Крутящий момент Mz2 в сечении II численно равен алгебраической сумме моментов M1 и M1, т.е. Mz2 =200-300=-100 нм, а его знак зависит от соотношения этих моментов.
Аналогичным образом вычисляется крутящий момент Mz3 в сечении III: Mz3 =200-300+500=400 нм.
Изменение крутящих моментов по длине вала покажем с помощью эпюры крутящих моментов. На рис. 5.4, б показана такая эпюра для стержня, изображенного на рис. 5.4, а.
Каждая ордината эп. Mk в принятом масштабе равна величине крутящего момента, действующего в том поперечном сечении бруса, которому соответствует эта ордината.
В сечении, в котором к брусу приложен внешний скручивающий момент, ордината эпюры изменяется скачкообразно на величину, равную значению этого момента.
Следует учитывать, что наибольший внешний скручивающий момент, приложенный к брусу, не всегда равен наибольшему крутящему моменту, по которому ведется расчет бруса на прочность и жесткость.
Построить эпюру крутящих моментов для жестко защемленного стержня (рис.5.4.1, а).
Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил.
1. Намечаем характерные сечения.
2. Определяем крутящий момент в каждом характерном сечении.
3. По найденным значениям строим эпюру (рис.5.4.1, б).
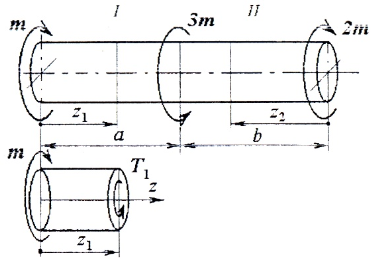
Рассмотрим расчетную схему вала, нагруженного двумя сосредоточенными моментами М и 2М и распределенными по длине: т (рис. 5.4.2).
Рис. 5.4.2. Построение эпюры внутренних крутящих моментов:
а – расчетная схема; б – первый участок, левая часть; в – второй участок, левая часть;
г – третий участок, правая часть; д – эпюра внутренних крутящих моментов
В исходных сечениях 1–1; 2–2; 3–3 задаются положительными значениями внутренних крутящих моментов М1, М2, М3. Пусть .
Для первого участка (рис. 5.4.2, б):
Для второго участка (рис. 5.4.2, в):
Для третьего участка (рис. 5.4.2, г):
Границы измерения параметра х3 в следующей системе координат:
Отмеченные значения ординат откладываются на эпюре внутренних крутящих моментов (рис. 5.4.2, д).
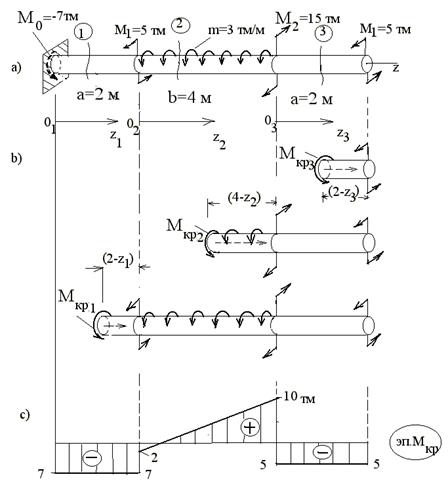
На рис. 5.4.3 дан пример определения по методу сечений внутренних крутящих моментов по участкам и внизу (ри.5.4.3, с) изображена суммарная эпюра Мкр.
Рис.5.4.3. a) заданный стержень с нагрузкой; b) отсеченные части стержня;
с) эпюра крутящих моментов.
В данном случае для консольного стержня вести вычисления удобно, идя справа налево, начав их с 3–го участка.
Участок 3(рис. 5.4.3, b). Неизвестный момент Mкр3 прикладываем к отсеченной части как положительный, после чего пишем условие равновесия отсеченной части:
Участок 2(рис. 5.4.3, b). Положение сечения фиксируем с помощью местной координаты z2 :
Читайте также: Не включается компрессор кондиционера мазда 3 2011
Участок 1(рис. 5.4.3, b):
Найдем реактивный момент в заделке M0 из условия равновесия всего стержня Σmz =0, это дает M0 +3∙4+5+5-15=0 и M0 = -7 тм, что совпадает с Mкр1 , найденным на участке 1 по методу сечений. Этого конечно следовало ожидать, так как по существу реактивный момент – это внутреннее усилие, действующее в поперечном сечении, где соединены торец стержня и заделка.
Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать
iSopromat.ru
Пример решения задачи на построение эпюры скручивающих моментов при кручении вала по силовым участкам методом сечений.
Задача
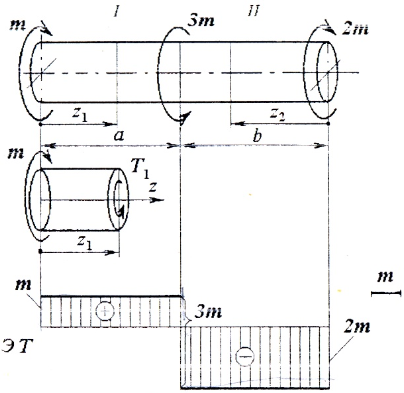
Построить эпюру крутящих моментов для следующей расчетной схемы вала:
На рассматриваемом валу можно выделить два силовых участка.
Границами участков являются сечения, в которых приложены скручивающие моменты.
Используя метод сечений и правило знаков при кручении, определяем величины крутящих моментов на I и II участках:
Следует отметить, что значения крутящего момента не зависят от того, правую или левую от проведенного сечения часть вала мы рассматриваем.
Например, для второго участка, рассматривая правую от сечения часть вала, получим:
По полученным значениям строится эпюра крутящих моментов:
Если к валу приложены только сосредоточенные скручивающие моменты, эпюра крутящего момента в пределах каждого участка вычерчивается прямыми, параллельными базовой линии.
В тех сечениях, где к валу приложены крутящие моменты mi, на эпюре T имеют место скачки, по модулю равные величине моментов mi.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать
Кручение
Видео:Сопромат. Построение эпюр вала при кручении. Я в вк https://vk.com/id4682924Скачать
Общие положения. Эпюры крутящих моментов
Кручению в основном подвергаются брусья круглого сечения, к которым относятся валы двигателей, оси машин и т.п., а также кручение могут испытывать пространственные конструкции.
Кручением называют вид деформации тела, возникающий при воздействии на него пары сил, лежащей в плоскости, поперечной его продольной оси.
Момент этой пары называют вращающим моментом Мвр. При установившемся (равномерном) вращении вала, если пренебречь трением в подшипниках, в которых вращается вал, должно соблюдаться условие равновесия ?МВр = 0.
Рис. 11.1. Кручение бруса круглого сечения (вала):
Момент внутренней пары сил, действующей в плоскости поперечного сечения бруса, называют крутящим моментом Мкр. Других внутренних силовых факторов при таком нагружении в сечениях вала не возникает.
Когда на вал насажено несколько шкивов (рис. 11.1), передающих вращение другим элементам машины, крутящий момент меняется по длине вала. Для наглядного представления об изменениях крутящих моментов в разных сечениях вала строят эпюру крутящих моментов.
Рассмотрим построение эпюры крутящих моментов для вала, передающего вращение через шкивы. Крутящие моменты определяют методом сечений. Для этого назначают положения сечений в промежутках от подшипника до шкива и между соседними шкивами. В рассматриваемом сечении мысленно рассекают брус на две части и одну из частей отбрасывают, воздействие отброшенной части заменяют внутренним усилием МКр (крутящим моментом) и определяют его значение из уравнения равновесия для оставшейся части.
Читайте также: Ремонт тормозных валов bpw
Крутящий момент, возникающий в поперечном сечении бруса, численно равен алгебраической сумме крутящих моментов, приложенных с одной стороны от рассматриваемого сечения.
Правило знаков: если при взгляде от сечения крутящий момент направлен по ходу часовой стрелки, его считают положительным, если направлен против часовой стрелки — отрицательным.
Определив значения крутящих моментов во всех сечениях, строят эпюру крутящих моментов по длине оси z.
Пример 11.1. Определить значения крутящих моментов и построить эпюру их распределения по длине вала (рис. 11.2). На вал передаются вращающие моменты: М = 500 Н м; Мг = 1600 Н-м; Мъ = 800 Н-м; Ма = 300 Н-м.
Решение. Смотрим справа налево, если момент создает вращение по часовой стрелке, принимаем его со знаком «плюс», если против часовой стрелки — знак «минус». Для установившегося равномерного вращения сумма всех внешних вращающих моментов (см. рис. 11.2) равна нулю: ?Мвр = 0; М — Mi + Мъ + Ма = 0; 500 — 1600 + 800 + 300 = 0.
Поочередно рассматриваем сечения, обозначенные на рис.
11.2. Алгебраическая сумма внешних моментов, взятых с левой или с правой стороны от сечения, равна крутящему моменту в сечении.
В сечении 1-1: Л/кр,1 = 0; в сечении 2-2: Мер,2 = М = 500 Н-м; в сечении 3-3: Мкр,ъ = М- Мг = 500- 1600 = -1100 Н-м; в сечении 4-4: Мф,4 = М- Мг + Мъ= 500 — 1600 + 800 = -300 Н-м; в сечении 5- 5: Мкр,5 = М-Mi + Мъ+Ма = 500-1600 + 800 + 300 = 0.
По найденным значениям строим эпюру крутящих моментов. Положительные значения моментов откладываем вниз от базисной линии, а отрицательные — вверх. В пределах каждого участка между точками, в которых приложены смежные вращающие моменты, значение крутящего момента постоянно.
Из эпюры следует, что наибольший крутящий момент Мкр = -1100 Н-м. Знак показывает направление вращения.
Рис. 11.2. К примеру 11.1. Схема вала, загруженного вращающими моментами, и эпюра крутящих моментов
Задача 11.1. Построить эпюру крутящих моментов для вала, изображенного на рис. 11.3. Вращающие моменты: М = 1450 Н м; М2 = 600 Н м; Мз = 2050 Н м.
Рис. 11.3. К задаче 11.1. Схема действия вращающих моментов на вал
- Свежие записи
- Чем отличается двухтактный мотор от четырехтактного
- Сколько масла заливать в редуктор мотоблока
- Какие моторы бывают у стиральных машин
- Какие валы отсутствуют в двухвальной кпп
- Как снять стопорную шайбу с вала
📹 Видео
Кручение валаСкачать
11. Кручение ( практический курс по сопромату )Скачать
КРУЧЕНИЕ. ЭПЮРЫ ЗАКРУЧИВАНИЯ. Углы поворота. СопроматСкачать
Построение эпюры крутящих моментовСкачать
БАЛКА - 90 СТУДЕНТОВ САМОСТОЯТЕЛЬНО СТРОЯТ ЭПЮРЫ после просмотра этого видео!Скачать
СОПРОМАТ. Тайные знания!!! Решение задачи о кручении бруса.Скачать
Изгиб с кручениемСкачать
РАСТЯЖЕНИЕ-СЖАТИЕ. Построение эпюр. Сопромат.Скачать
Кручение. Расчет составного вала кольцевого сечения.Скачать
Кручение. Часть 6 Жесткость валаСкачать
Почему число 37 встречается повсюду? [Veritasium]Скачать
Прочность и жесткость валов. Часть 6: Эпюры моментов выходного вала (цилиндрическая передача).Скачать
Вал. Расчет на прочность при косом изгибе и крученииСкачать
Изгиб с кручением. Расчет на прочностьСкачать
Прикладная механика и механика, Заказать задачиСкачать
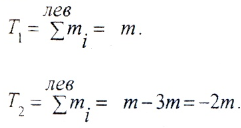
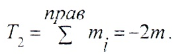
![Почему число 37 встречается повсюду? [Veritasium]](https://i.ytimg.com/vi/26meYYVE2Yg/0.jpg)
