Эпюра крутящих моментов вала это

Кручение стержня вызывается парами сил (сосредоточенными или распределенными), плоскость действия которых перпендикулярна продольной оси стержня. При кручении в поперечном сечении стержня возникает лишь один силовой фактор – крутящий момент M_к.

Согласно методу сечений величина и направление крутящего может быть найдены из уравнения равновесия моментов относительно оси стержня, составленного для оставленной части. То есть, крутящий момент в сечении численно равен алгебраической сумме моментов пар сил, приложенных по одну сторону от рассматриваемого сечения, относительно продольной оси стержня.

Крутящий момент считается положительным, если при взгляде на сечение со стороны внешней нормали он поворачивает сечение по ходу часовой стрелки и отрицательным — в противном случае.
При построение эпюры крутящих моментов положительные значения откладываются вверх от горизонтальной базовой линии, а отрицательные – вниз.

Это правило знаков условное и не совпадает с принятыми правилами знаков моментов, углов поворота в теоретической механике и математике, поскольку связано не с системой координат, а с видом деформации оставленной части.

Крутящий момент для сечения можно выразить так: $$M _к(x) = \sum M _ + \sum \int m _i(x)\cdot dx$$

Распределенный крутящий момент m может быть постоянной или переменной интенсивности. Для постоянного распределенного момента m это выражение примет вид: $$M _к(x) = \sum M _ + \sum m _i(x)\cdot (x- L_ ) — \sum m _i(x)\cdot (x- L_ )$$

где L_mн и L_mк – расстояние от начала координат до начала и до конца распределенного момента соответственно.

Дифференциальная зависимость внутренних усилий от распределенной нагрузки m:

Общий порядок расчета и построения эпюры.

1. Намечаем характерные сечения стержня.
2. Определяем крутящий момент в каждом характерном сечении.
3. По найденным значениям моментов строим эпюру.

Построение эпюр крутящих моментов (пример)

Пусть прямолинейный стержень нагружен внешними сосредоточенными крутящими моментами M_кв1=-30кН·м, M_кв2=50 кН·м, и распределенным моментом m₁=10кН. Реакции левой опоры можно не определять, т.к. в этом примере можно ограничиться рассмотрением лишь сил, приложенных к правым оставленным частям (справа от сечений).

1. Число характерных сечений — 6
Для заданного консольного стержня вычисления удобно вести, идя справа налево, начав их с 1–го сечения.

2. Проведем сечение 1. Определим крутящий момент в текущем сечении:

3. Проведем сечение 2. Отбросим левую часть, заменим ее действие крутящим моментом M_к2 и составим уравнение равновесия в моментах относительно оси бруса. Из уравнения равновесия получаем выражение для крутящего момента в сечении 2:

3. Проведем сечение 3, отбрасываем левую часть, составляем уравнение равновесия и получаем:

4. Аналогично для сечения 4:

7. По полученным значения строим эпюру крутящих моментов (см. рис.).

Скачок на левом конце эпюры дает величину опорного момента (реактивного момента в заделке) M_к6, так как реактивный момент – это внутреннее усилие, действующее в поперечном сечении, где соединены торец стержня и заделка.

Правила контроля правильности эпюр крутящих моментов

Для эпюр крутящих моментов характерны некоторые закономерности, знание которых позволяет оценить правильность построений.

• Эпюры крутящих моментов всегда прямолинейные.
• На участке, где нет распределенных моментов, эпюра M_к – прямая, параллельная оси; а на участке с распределенными моментами – наклонная прямая.
• Под точкой приложения сосредоточенного момента на эпюре M_к будет скачок на величину этого момента.

Дополнительно

Еще один вариант построения эпюры крутящих моментов с использованием компьютера найдете на этой странице.

1 В технике употребляется терминология «винт с правой резьбой» или «винт с левой резьбой». На винт с правой резьбой гайка навертывается при вращении по часовой стрелке (т.е прикладываем положительный момент M_к ), а свинчивание гайки происходит при вращении влево (т.е прикладываем отрицательный крутящий момент ).

Читайте также: Как снять пружинную стопорную шайбу с вала

Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

Техническая механика

Сопротивление материалов

Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать

Деформация кручения

Построение эпюр крутящих моментов

Для наглядного изображения распределения крутящих моментов вдоль оси бруса строят эпюры крутящих моментов — графическое отображение величины крутящих моментов на каждом участке бруса.

Крутящий момент в сечениях бруса определяется с помощью метода сечения. Так как равномерно вращающийся или неподвижный вал находится в равновесии, очевидно, что внутренние силы, возникающие в поперечном сечении, должны уравновешивать внешние моменты, действующие на рассматриваемую часть бруса. Отсюда следует, что крутящий момент в любом поперечном сечении численно равен алгебраической сумме внешних моментов, приложенных к брусу справа или слева от сечения.

Эпюры крутящих моментов дают возможность определить опасное сечение. В частности, если брус имеет постоянное поперечное сечение по всей длине, то опасными будут сечения на участке, где возникает наибольший крутящий момент.

Следует очень внимательно отнестись к определению знаков крутящего момента. Крутящий момент считается положительным, если при взгляде со стороны сечения результирующий момент внешних пар сил, приложенных к рассматриваемой части бруса, будет направлен против часовой стрелки, и наоборот (это положение условно и принимается для облегчения проверки расчетов, выполненных несколькими исполнителями).

Рассматривая величины крутящих моментов, действующих в каждом конкретном сечении бруса, полагаем, что в сечении, где приложен вращающий (скручивающий) момент, значения крутящего момента изменяются скачкообразно (принцип смягченных граничных условий).

Пример построения эпюры крутящих моментов

Силовая передача (трансмиссия), изображенная на рис. 2 состоит из вала, на котором размещены три шестерни — одна ведущая ( А ) и две ведомые ( В и С ).
К шестерням приложены вращающие моменты: Р_А = 300 Нм, Р_В = 120 Нм, Р_С = 180 Нм.
Построим эпюру крутящих моментов для этой силовой передачи.

Решение

Очевидно, что свободные концы вала, (вращающиеся в подшипниках) не подвержены действию вращающих моментов, т. е. крутящие моменты на участках 1 и 4 равны нулю.
К шестерне А приложен вращающий момент 300 Н м, следовательно в сечении, расположенном под этой шестерней скачкообразно возникает крутящий момент, равный 300 Нм, и величина этого момента сохраняется неизменной по всем сечениям участка 2 (до шестерни В ).

К шестерне В приложен вращающий момент 120 Нм, который направлен в противоположную сторону от ведущего скручивающего момента, приложенного к шестерне А . Следовательно крутящий момент на участке 3 будет равен разности крутящих моментов, приложенных к шестерням А и В . На эпюре это отобразится в виде ступени величиной 120 Нм, расположенной напротив сечения, где размещена шестерня В .
На всем протяжении участка 3 величина этого крутящего момента будет сохраняться неизменной, до сечения, расположенного под шестерней С .

К шестерне С приложен вращающий момент 180 Нм, направление которого противоположно моменту, приложенному к ведущей шестерне А , поэтому, начиная с сечения под шестерней С , крутящий момент будет равен разнице между скручивающим моментом шестерни А и моментами, приложенными к шестерням В и С , т. е.
М_КРс = Т_А — Т_В — Т_С = 300 — 120 — 180 = 0 Нм, и величина этого момента будет распространяться на весь участок 4 , расположенный за шестерней С .

Читайте также: Вибратор глубинный с гибким валом булава

Построив эпюру крутящих моментов, действующих в сечениях вала данной силовой передачи как показано на рис. 2 , отмечаем, что максимальной величины — 300 Нм крутящий момент достигает на участке 2 , т. е. этот участок и является критическим (наименее надежным).

Теперь попробуем изменить расположение шестерен на валу, разместив ведущую шестерню А между ведомыми шестернями В и С , как показано на рис. 3 . Приложенные к шестерням вращающие моменты оставим без изменения и построим эпюру крутящих моментов для измененной конструкции ( рис. 3 ).

Из полученной эпюры видно, что на участке 2 (между шестернями В и А ) крутящий момент равен —120 Нм, на участке 3 — +180 Нм, а на участках 1 и 4 крутящие моменты равны нулю, как и в предыдущей конструкции. И если в рассмотренной ранее конструкции максимальный крутящий момент достигал 300 Нм, то теперь его величина снизилась до 180 Нм.
Рациональным размещением шестерен на валу силовой передачи мы смогли значительно уменьшить максимальный крутящий момент, возникающий в сечениях этого вала, повысив надежность передачи. При этом передаточные отношения и функционал самой передачи не изменились.

Материалы раздела «Деформация кручения»:

Видео:Сопромат. Практическое занятие №1.4Скачать

Построение эпюр крутящих моментов

Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов M_k (M_z) в поперечных сечениях по длине вала. Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.

В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣM_z=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 5.1, крутящий момент M_z в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M₁|=|M₂|.

В более сложных случаях, когда к валу приложено несколько внешних моментов, крутящие моменты M_k в поперечных сечениях различных участков вала неодинаковы.

На основании метода сечений крутящий момент в произвольном поперечном сечении вала численно равен алгебраической сумме внешних скручивающих моментов, приложенных к валу по одну сторону от рассматриваемого сечения.

При расчетах на прочность и жесткость знак крутящего момента не имеет никакого значения, но для удобства построения эп. M_k примем следующее правило знаков: крутящий момент считается положительным, если при взгляде в торец отсеченной части вала действующий на него момент представляется направленным по ходу часовой стрелки (рис.5.2).

В технике употребляется терминология « винт с правой нарезкой» или «…с левой нарезкой…», причем правый винт наиболее распространен, являясь стандартом. Полезно заметить, что при навинчивании гайки на правый винт мы прикладываем положительный момент M_кр , а при свинчивании гайки – отрицательный.

При наличии распределенной моментной нагрузки m (рис.5.3) крутящие моменты М_К связаны дифференциальной зависимостью

из которой вытекает следующая формула:

где – крутящий момент в начале участка.

Согласно формуле (5.2) на участках с равномерно распределенной нагрузкой m крутящий момент изменяется по линейному закону. При отсутствии погонной нагрузки (m = 0) крутящий момент сохраняет постоянное значение (М_К = М_Ко = const). В сечениях, где к валу приложены сосредоточенные скручивающие моменты, на эпюре М_К возникают скачки, направленные вверх, если моменты направлены против часовой стрелки, либо вниз – при обратном направлении моментов.

Читайте также: Съемник для крестовин карданного вала газель

На рис. 5.4, а изображен стержень, жестко защемленный в правом концевом сечении, к которому приложены три внешних скручивающих момента.

В нашем случае крутящие моменты в их поперечных сечениях удобно выражать через внешние моменты, приложенные со стороны свободного конца бруса.

Это позволяет определять крутящие моменты, не вычисляя реактивного момента, возникающего в заделке.

Крутящий момент M_z1 в сечении I численно равен M₁=200 нм и, согласно принятому правилу знаков, положителен.

Крутящий момент M_z2 в сечении II численно равен алгебраической сумме моментов M₁ и M₁, т.е. M_z2 =200-300=-100 нм, а его знак зависит от соотношения этих моментов.

Аналогичным образом вычисляется крутящий момент M_z3 в сечении III: M_z3 =200-300+500=400 нм.

Изменение крутящих моментов по длине вала покажем с помощью эпюры крутящих моментов. На рис. 5.4, б показана такая эпюра для стержня, изображенного на рис. 5.4, а.

Каждая ордината эп. M_k в принятом масштабе равна величине крутящего момента, действующего в том поперечном сечении бруса, которому соответствует эта ордината.

В сечении, в котором к брусу приложен внешний скручивающий момент, ордината эпюры изменяется скачкообразно на величину, равную значению этого момента.

Следует учитывать, что наибольший внешний скручивающий момент, приложенный к брусу, не всегда равен наибольшему крутящему моменту, по которому ведется расчет бруса на прочность и жесткость.

Построить эпюру крутящих моментов для жестко защемленного стержня (рис.5.4.1, а).

Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил.

1. Намечаем характерные сечения.

2. Определяем крутящий момент в каждом характерном сечении.

3. По найденным значениям строим эпюру (рис.5.4.1, б).

Рассмотрим расчетную схему ва­ла, нагруженного двумя сосредоточенными моментами М и 2М и распределенными по длине: т (рис. 5.4.2).

Рис. 5.4.2. Построение эпюры внутренних крутящих моментов:

а – расчетная схема; б – первый участок, левая часть; в – второй участок, левая часть;

г – третий участок, правая часть; д – эпюра внутренних крутящих моментов

В исходных сечениях 1–1; 2–2; 3–3 задаются положительными зна­чениями внутренних крутящих мо­ментов М₁, М₂, М₃. Пусть .

Для первого участка (рис. 5.4.2, б):

Для второго участка (рис. 5.4.2, в):

Для третьего участка (рис. 5.4.2, г):

Границы измерения параметра х₃ в следующей системе координат:

Отмеченные значения ординат откладываются на эпюре внутренних крутящих моментов (рис. 5.4.2, д).

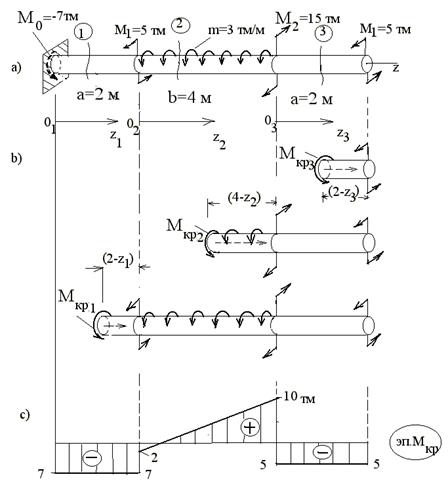
На рис. 5.4.3 дан пример определения по методу сечений внутренних крутящих моментов по участкам и внизу (ри.5.4.3, с) изображена суммарная эпюра М_кр.

Рис.5.4.3. a) заданный стержень с нагрузкой; b) отсеченные части стержня;

с) эпюра крутящих моментов.

В данном случае для консольного стержня вести вычисления удобно, идя справа налево, начав их с 3–го участка.

Участок 3(рис. 5.4.3, b). Неизвестный момент M_кр3 прикладываем к отсеченной части как положительный, после чего пишем условие равновесия отсеченной части:

Участок 2(рис. 5.4.3, b). Положение сечения фиксируем с помощью местной координаты z₂ :

Участок 1(рис. 5.4.3, b):

Найдем реактивный момент в заделке M₀ из условия равновесия всего стержня Σm_z =0, это дает M₀ +3∙4+5+5-15=0 и M₀ = -7 тм, что совпадает с M_кр1 , найденным на участке 1 по методу сечений. Этого конечно следовало ожидать, так как по существу реактивный момент – это внутреннее усилие, действующее в поперечном сечении, где соединены торец стержня и заделка.

• Свежие записи
  • Чем отличается двухтактный мотор от четырехтактного
  • Сколько масла заливать в редуктор мотоблока
  • Какие моторы бывают у стиральных машин
  • Какие валы отсутствуют в двухвальной кпп
  • Как снять стопорную шайбу с вала
  • Правообладателям
  • Политика конфиденциальности

  
  

  источники:

  https://evakuatorinfo.ru/epyura-krutyaschih-momentov-vala-eto

  📸 Видео

  Сопромат. Построение эпюр вала при кручении. Я в вк https://vk.com/id4682924Скачать

  

  ПЗ Часть 1 Построение эпюры крутящего моментаСкачать

  

  КРУЧЕНИЕ. ЭПЮРЫ ЗАКРУЧИВАНИЯ. Углы поворота. СопроматСкачать

  

  Построение эпюры крутящих моментовСкачать

  

  11. Кручение ( практический курс по сопромату )Скачать

  

  Кручение. Построение эпюр крутящих моментов в сопротивлении материалов.Скачать

  

  Кручение. Расчет составного вала кольцевого сечения.Скачать

  

  ПЗ Часть 3 Эпюра крутящего моментаСкачать

  

  9.1 Расчет валов приводаСкачать

  

  БАЛКА - 90 СТУДЕНТОВ САМОСТОЯТЕЛЬНО СТРОЯТ ЭПЮРЫ после просмотра этого видео!Скачать

  

  Изгиб с кручениемСкачать

  

  Кручение валаСкачать

  

  Вот для чего нужно строить эпюры в сопромате!Скачать

  

  Прочность и жесткость валов. Часть 6: Эпюры моментов выходного вала (цилиндрическая передача).Скачать

  

  Пример построения эпюры крутящего момета ЭТСкачать

  

  Кручение. Часть 1 Общие сведенияСкачать

  

  Расчет вала на изгиб с кручениемСкачать