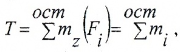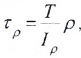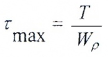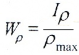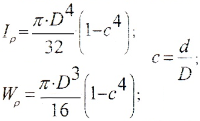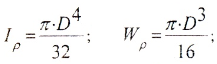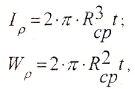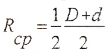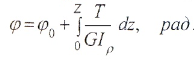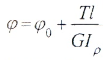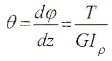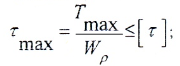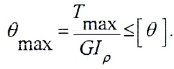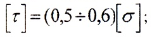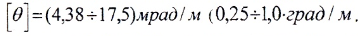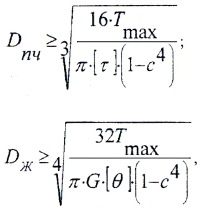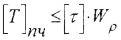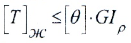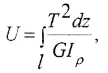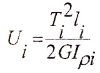Эпюра вала при кручении

На этой странице приведен еще один пример решения задачи по Сопромату, в которой необходимо произвести расчет вала переменного сечения (ступенчатого), нагруженного крутящими моментами. По результатам расчетов необходимо подобрать размеры вала, а также определить максимальную деформацию вала на скручивание (угол закручивания).

Результаты расчетов оформлены эпюрами крутящих моментов, касательных напряжений и углов закручивания бруса.

Студентам технических специальностей ВУЗов в качестве методической помощи предлагаются к скачиванию готовые варианты контрольных работ по сопромату (прикладной механике). Представленные задания и примеры их решения предназначены, в частности, для учащихся Алтайского Государственного технического университета.
Варианты контрольных работ можно скачать в формате Word для ознакомления с порядком решения заданий, или для распечатывания и защиты (при совпадении вариантов).

Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

Расчет вала

Условие задачи:

К стальному валу, состоящему из 4-х участков длиной l₁…l₄ приложено четыре сосредоточенных момента М₁…М₄ (см. рис. 1 ).

Требуется:

Построить эпюру крутящих моментов М_кр , подобрать диаметр вала из расчета на прочность, построить эпюру максимальных касательных напряжений τ_max , построить эпюру углов закручивания φ вала и определить наибольший относительный угол закручивания вала.

Исходные данные:

Указания:

Вычертить схему вала в соответствии с исходными данными.
Знаки моментов в исходных данных означают: плюс – момент действует против часовой стрелки относительно оси Z , минус – по часовой стрелке (см. навстречу оси Z ). В дальнейшем значения моментов принимать по абсолютной величине.
Участки нумеровать от опоры.
Допускаемое касательное напряжение [ τ ] для стали принимать равным 100 МПа.

Решение:

1. Определим методом сечений значения крутящих моментов на каждом силовом участке от свободного конца вала.
Крутящий момент равен алгебраической сумме внешних моментов, действующих на вал по одну сторону сечения.

2. Подберем сечение вала из расчета на прочность при кручении по полярному моменту сопротивления для участка, где величина крутящего момента максимальная (без учета знака):

Так как для круглого сечения полярный момент равен: W_р = πD 3 /16 , то можно записать:

D ≥ 3 √ (16М_кр/π[τ]) ≥ 3√(16×12,2×10 3 /3,14×[100×10 6 ]) = 0,0855 м или D ≥ 85,5 мм.

( Здесь и далее знак «√» означает квадратный корень из выражения )

В соответствии со стандартным рядом, предусмотренным ГОСТ 12080-66, принимаем диаметр вала D = 90 мм.

3. Определим угол закручивания для каждого участка вала по формуле:

где
G – модуль упругости 2-го рода; для стали G = 8×10 10 Па;
I_p – полярный момент инерции (для круглого сечения I_р = πD 4 /32 ≈ 0,1D 4 , м 4 ).
Произведение G×I_р = 8×10 10 ×0,1×0,094 ≈ 524880 Н×м 2 – жесткость сечения данного вала при кручении.

Расчитываем углы закручивания на каждом участке:

Читайте также: Отклонение от параллельности валы

4. Определяем углы закручивания сечений вала, начиная от жесткой заделки (опоры):

5. Определяем максимальное касательное напряжение на каждом силовом участке по формуле:

6. Наибольший относительный угол закручивания Θ_max определим по формуле:

7. По результатам расчетов строим эпюры крутящих моментов М_кр , касательных напряжений τ_max и углов закручивания φ (см. рис. 2).

Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать

Тема 2.4. Кручение

Под кручением понимается такой вид деформации, когда в поперечных сечениях бруса действует только крутящий момент M_k, (другое обозначение T, M_z), а остальные силовые факторы (нормальная и поперечная силы и изгибающие моменты) отсутствуют.

Или другое определение кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рис.1).

Кручение возникает в валах, винтовых пружинах, в элементах пространственных конструкций и т.п.

Деформация кручения наблюдается если прямой брус нагружен внешними моментами (парами сил M), плоскости действия которых перпендикулярны к его продольной оси

В чистом виде деформация кручения встречается редко, обычно присутствуют и другие внутренние силовые факторы (изгибающие моменты, продольные силы).

Стержни круглого или кольцевого сечения, работающие на кручение, называют валами.

Внешние крутящие моменты передаются на вал в местах посадки на него шкивов, зубчатых колес, там, где поперечная нагрузка смещена относительно оси вала.

Мы будем рассматривать прямой брус только в состоянии покоя или равномерного вращения. В этом случае алгебраическая сумма всех внешних скручивающих моментов, приложенных к брусу, будет равна нулю.

При расчете брусьев, испытывающий деформацию кручения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от M_k), возникающих в брусе, и нахождение угловых перемещений в зависимости от внешних скручивающих моментов.

При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.

В ряде случаев величины внешних крутящих моментов определяются по величине потребляемой мощности и по скорости вращения вала. Если вал делает в минуту n оборотов (n- частота вращения, единицы измерения — об/мин.), то вращающий момент можно найти по формуле: М_вр=P/n,

эта формула дает значение момента в Н·м, если мощность выражена в Вт, а частота вращения n — об/мин.

§2. Построение эпюр крутящих моментов

Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов M_k (M_z) в поперечных сечениях по длине вала. Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.

Читайте также: Воздушный шланг для компрессора 16 25 мм армированный

В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣM_z=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 1, крутящий момент M_z в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M₁|=|M₂|.

Видео:Сопромат. Построение эпюр вала при кручении. Я в вк https://vk.com/id4682924Скачать

iSopromat.ru

Кручением называется такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент T.

Брусья, испытывающие кручение, принято называть валами.

Видео:Сопромат. Практическое занятие №1.4Скачать

Внутренний крутящий момент

Внутренние скручивающие моменты появляются под действием внешних крутящих моментов m_i, расположенных в плоскостях, перпендикулярных к продольной оси бруса.

Скручивающие моменты передаются на вал в местах посадки зубчатых колес, шкивов ременных передач и т.п.

Величина крутящего момента в любом сечении вала определяется методом сечений:

т.е. крутящий момент численно равен алгебраической сумме скручивающих моментов m_i, расположенных по одну сторону от рассматриваемого сечения.

Правило знаков внутренних скручивающих моментов:
Положительными принимаются внутренние моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки, при рассмотрении со стороны отброшенной части вала.

В технике наиболее широко используются валы круглого поперечного сечения.

Теория кручения круглых валов основана на следующих гипотезах:

1. поперечное сечение, плоское до деформации вала, остается плоским и после деформации;
2. радиусы, проведенные мысленно в любом поперечном сечении, в процессе деформации вала не искривляются.

Видео:КРУЧЕНИЕ. ЭПЮРЫ ЗАКРУЧИВАНИЯ. Углы поворота. СопроматСкачать

Напряжения при кручении

В поперечных сечениях вала при кручении имеют место только касательные напряжения.
Касательные напряжения, направленные перпендикулярно к радиусам, для произвольной точки, отстоящей на расстоянии ρ от центра, вычисляются по формуле:

где I_ρ — полярный момент инерции.
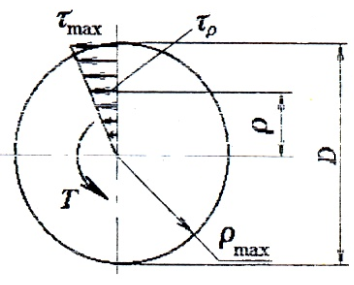
Эпюра касательных напряжений при кручении имеет следующий вид:

Касательные напряжения меняются по линейному закону и достигают максимального значения на контуре сечения при ρ= ρ_max:

Здесь:

— полярный момент сопротивления.
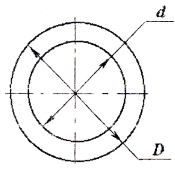
Геометрические характеристики сечений:
а) для полого вала:


б) для вала сплошного сечения (c=0)

в) для тонкостенной трубы (t 0,9)

где

— радиус срединной поверхности трубы.

Видео:Построение эпюры крутящих моментовСкачать

Деформации

Деформации валов при кручении заключаются в повороте одного сечения относительно другого.

Угол закручивания вала на длине Z определяется по формуле:

Если крутящий момент и величина GI_ρ, называемая жесткостью поперечного сечения при кручении, постоянны, для участка вала длиной l имеем:

Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания:

Расчет валов сводится к одновременному выполнению двух условий:

1. условию прочности:
   
2. условию жесткости:
   

Для стальных валов принимается:

• допускаемое касательное напряжение
  
• допускаемый относительный угол закручивания
  

Используя условия прочности и жесткости, как и при растяжении – сжатии можно решать три типа задач:

Читайте также: Nissan primera p11 ремень генератора без компрессора

1. проверочный расчет, заключающийся в проверке выполнения условий прочности и жесткости при известных значениях крутящего момента, размеров и материала вала.
2. Проектировочный расчет, при котором вычисляются диаметры:
   
   при этом берется большее из найденных значений, а затем принимается стандартное значение по ГОСТ.
3. Определение грузоподъемности вала:
   • из условия прочности
     
   • из условия жесткости
     

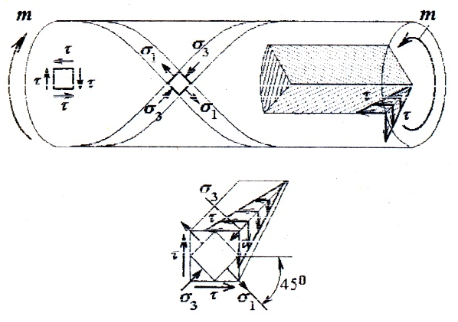
При кручении, наряду с касательными напряжениями в поперечных сечениях, в соответствии с законом парности, касательные напряжения возникают и в продольных сечениях. Таким образом, во всех точках вала имеет место чистый сдвиг.

Главные напряжения σ₁ = τ, σ₃ = -τ наклонены под углом α=±45 о к образующей.

Потенциальная энергия упругой деформации определяется по формуле

или для участка вала при постоянном T и GI_ρ

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:11. Кручение ( практический курс по сопромату )Скачать

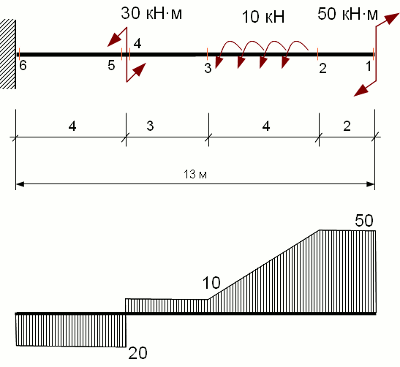
Пример построения эпюры крутящих моментов при кручении вала

Пусть прямолинейный стержень нагружен внешними сосредоточенными крутящими моментами Mкв1 = -30кН·м, Mкв2=50 кН·м, и распределенным моментом m1=10кН.

Реакции левой опоры можно не определять, т.к. в этом примере можно ограничиться рассмотрением лишь сил, приложенных к правым оставленным частям (справа от сечений).

Для заданного консольного стержня вычисления удобно вести, идя справа налево, начав их с 1–го сечения.

Проведем сечение 1. Определим крутящий момент в текущем сечении:

Проведем сечение 2. Отбросим левую часть, заменим ее действие крутящим моментом M к2 и составим уравнение равновесия в моментах относительно оси бруса. Из уравнения равновесия получаем выражение для крутящего момента в сечении 2:

M к2 = M к1 = M кв2 = 50 кНм

Проведем сечение 3, отбрасываем левую часть, составляем уравнение равновесия и получаем:

M к3 = M кв2 – m 1*4 = 50 – 10*4 = 10 кНм

Аналогично для сечения 4:

Также для сечения 5:

M к5= M к4-M кв1= 10 – 30 = -20 кНм

Для сечения 6:

По полученным значения строим эпюру крутящих моментов (см. рисунок).

Скачок на левом конце эпюры дает величину опорного момента (реактивного момента в заделке) M к6, так как реактивный момент – это внутреннее усилие, действующее в поперечном сечении, где соединены торец стержня и заделка.

Правила контроля правильности эпюр крутящих моментов

Для эпюр крутящих моментов характерны некоторые закономерности, знание которых позволяет оценить правильность построений.

• Эпюры крутящих моментов всегда прямолинейные.
• На участке, где нет распределенных моментов, эпюра M к – прямая, параллельная оси; а на участке с распределенными моментами – наклонная прямая.
• Под точкой приложения сосредоточенного момента на эпюре M к будет скачок на величину этого момента.

• Свежие записи
  • Чем отличается двухтактный мотор от четырехтактного
  • Сколько масла заливать в редуктор мотоблока
  • Какие моторы бывают у стиральных машин
  • Какие валы отсутствуют в двухвальной кпп
  • Как снять стопорную шайбу с вала
  • Правообладателям
  • Политика конфиденциальности

  Механика © 2023
  Информация, опубликованная на сайте, носит исключительно ознакомительный характер

  
  

  источники:

  https://evakuatorinfo.ru/epyura-vala-pri-kruchenii

  📸 Видео

  Кручение валаСкачать

  

  Кручение. Часть 6 Жесткость валаСкачать

  

  Сопротивление материалов. Лекция: кручение круглого стержняСкачать

  

  Правило знаков при крученииСкачать

  

  Кручение. Часть 1 Общие сведенияСкачать

  

  Кручение. Расчет составного вала кольцевого сечения.Скачать

  

  9.1 Расчет валов приводаСкачать

  

  Кручение зажатого валаСкачать

  

  Кручение. Построение эпюр крутящих моментов в сопротивлении материалов.Скачать

  

  БАЛКА - 90 СТУДЕНТОВ САМОСТОЯТЕЛЬНО СТРОЯТ ЭПЮРЫ после просмотра этого видео!Скачать

  

  Прочность и жесткость валов. Часть 6: Эпюры моментов выходного вала (цилиндрическая передача).Скачать

  

  ПЗ Часть 1 Построение эпюры крутящего моментаСкачать