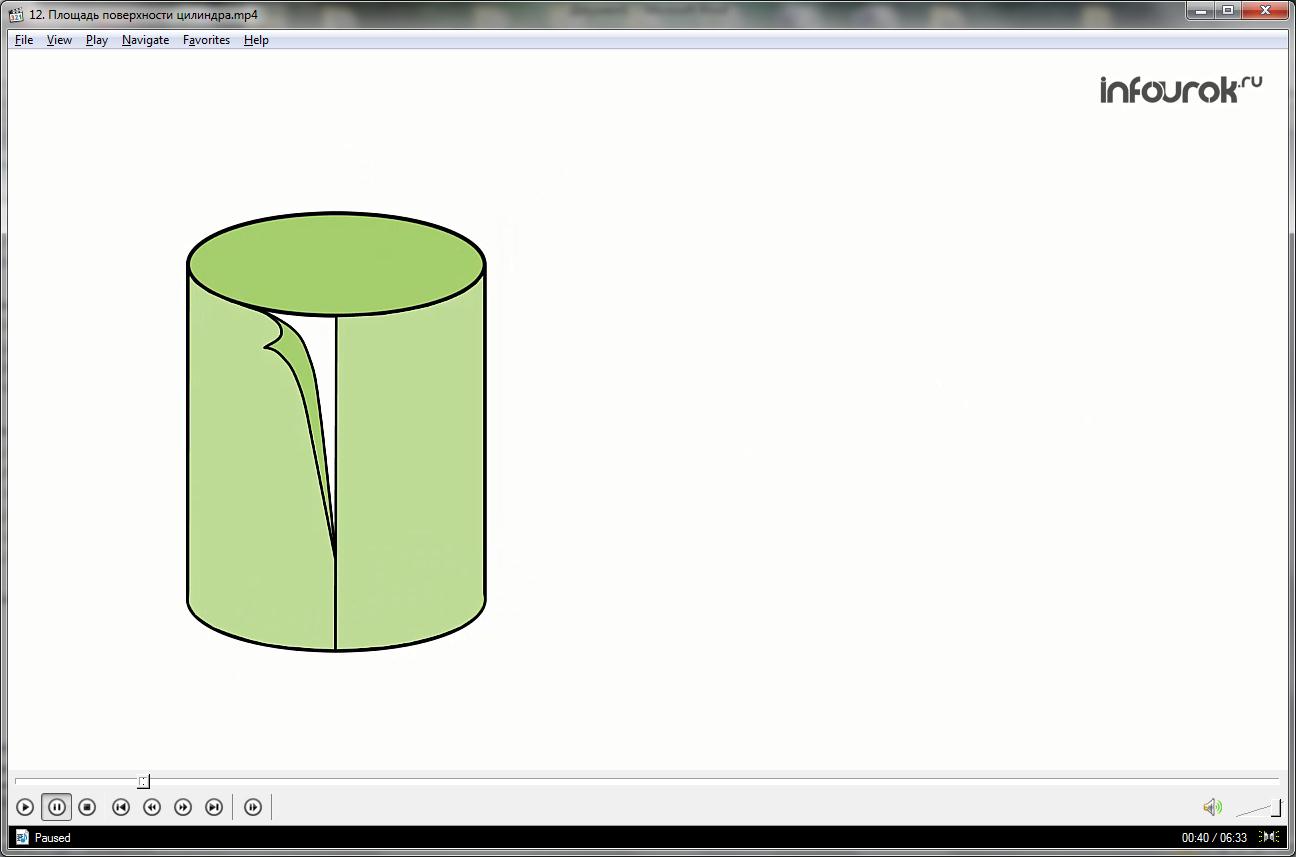
Поверхность цилиндра состоит из боковой поверхности, и оснований цилиндра, которые представляют собой два круга.
Длина образующей боковой поверхности называется высотой цилиндра (АВ), а радиус основания — радиусом цилиндра.
Попробуем разрезать боковую поверхность нашего цилиндра по образующей АВ так, чтобы все образующие оказались в плоскости α.
В результате в плоскости α получился прямоугольник ABCD. Этот прямоугольник представляет собой развертку боковой поверхности цилиндра.
Сторона AD – развертка окружности основания цилиндра, а высота АВ — образующей цилиндра.
AD= (формула длины окружности)
где r — радиус окружности, h — высота цилиндра.
За площадь боковой поверхности цилиндра принимается площадь ее развертки, т.е. площадь прямоугольника АВСD.
Площадь прямоугольника находится по формуле:
площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра.
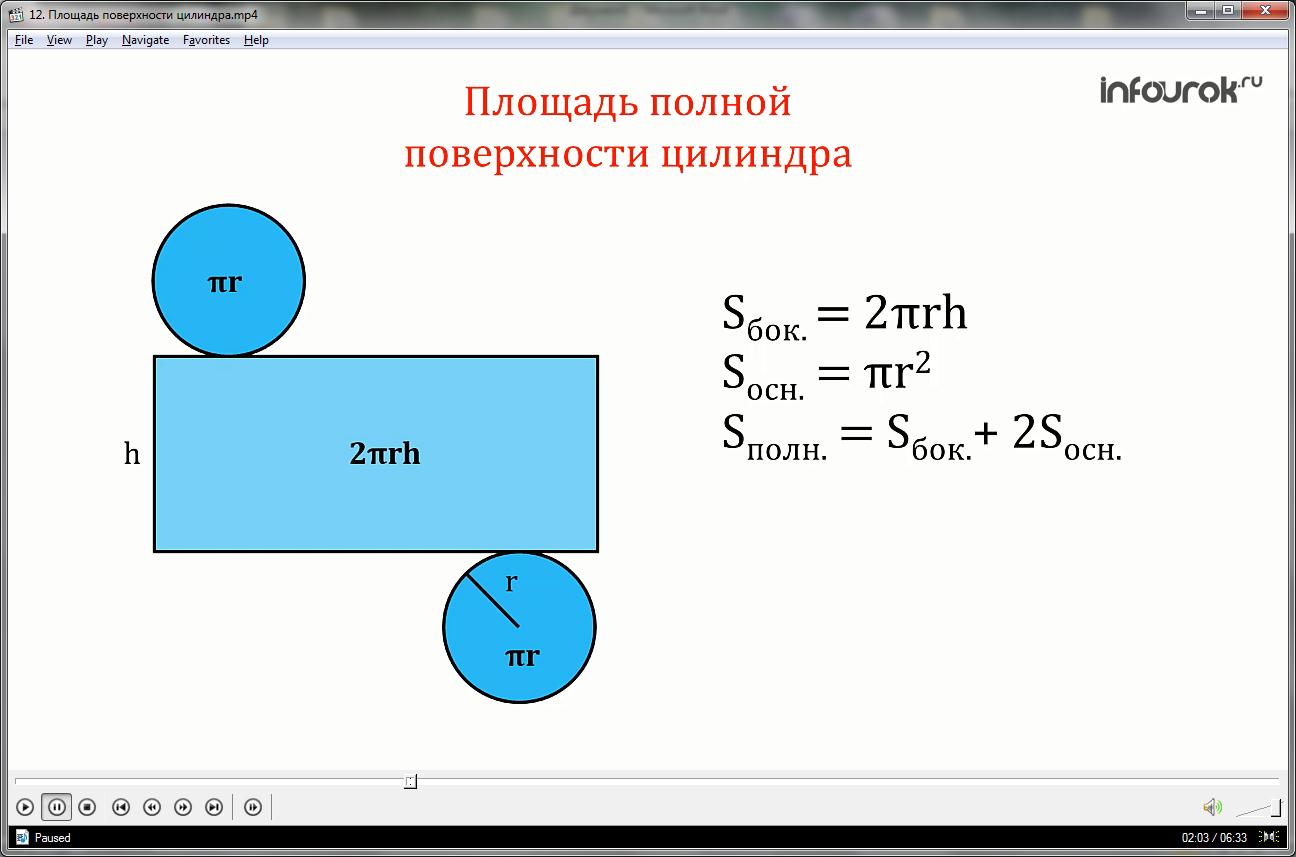
Найдем площадь полной поверхности цилиндра.
Цилиндр состоит из боковой поверхности и двух оснований.
Площадь полной поверхности цилиндра равна сумме площади двух оснований и боковой поверхности.
Так как основания в цилиндре равны, то полная его площадь будет рассчитываться по формуле:
Полученные знания применим при решении задач.
Трубка цилиндрической формы получается из прямоугольника. Вычислите радиус основания, если длина прямоугольника равна 16 см, ширина – 12см.
Так как трубка получается из прямоугольника, то его длинна – это есть длина окружности.
Найдем радиус окружности: (отношение длины окружности к двум пи)
Дано: цилиндр, ABCD-осевое сечение, АС=48 см, ACD= 60º.
Найти: а) СD — высота, б) АО — радиус, в) Sосн.
а)1.Рассмотрим осевое сечение АВСD.
ABCD — прямоугольник (по условию), значит
АС — гипотенуза, СD — катет, лежащий против угла в 30⁰.
Он равен половине гипотенузы
АО – радиус основания цилиндра.
АD – диаметр основания цилиндра. Поэтому, найдем диаметр по формуле
У отдельных изваяний, оставленных нам древнеегипетской культурой, можно видеть зажатые в руках объекты цилиндрической формы, предназначение которых историкам непонятно.
В 1976 году в Закавказье обнаружена старинная рукопись «Тайны Жизни и Смерти», в которой содержалась информация о Лунном и Солнечном цилиндрах, изготовленных из цинка и меди с определенным внутренним наполнением.
Было установлено, что цилиндры Фараона, так они называются, обладают широчайшим спектром благотворного воздействия на организм человека.
В него входят: помощь при сердечно-сосудистых заболеваниях, нейротрофических, гипертонии, болезнях выводящих путей, астме, бессоннице, головных болях, а также в качестве средства для снятия стрессов и профилактики атеросклероза.
Согласно мнению ряда врачей, Цилиндры Фараона представляют собой уникальный, самонастраивающийся на каждого человека, физиотерапевтический прибор, созданный гением древнеегипетских ученых.
Исследования показали, что воздействие Цилиндров Фараона переводит организм в иное, более «высокое» энергетическое состояние, при котором активнее протекают восстановительные процессы, способствующие гармонизации всего организма.
| Инфоурок |
| 07.11.2014 |
| Геометрия |
| Видеоурок |
| 11838 |
| 998 |
© 2021 Проект «Уроки математики»
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.
Читайте также: Lancer 9 пропуски зажигания 4 цилиндр
Видео:Видеоурок по математике "Цилиндр"Скачать

Разработка на тему «Цилиндр»
Ищем педагогов в команду «Инфоурок»
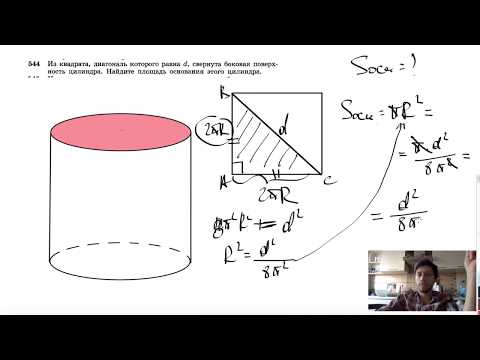
Видео:№544. Из квадрата, диагональ которого равна d, свернута боковая поверхность цилиндра.Скачать
Содержание
Стереометрия − это раздел геометрии, в котором изучаются фигуры в пространстве. Основными фигурами в пространстве являются точка, прямая и плоскость. В стереометрии появляется новый вид взаимного расположения прямых: скрещивающиеся прямые. Это одно из немногих существенных отличий стереометрии от планиметрии, так как во многих случаях задачи по стереометрии решаются путем рассмотрения различных плоскостей, в которых выполняются планиметрические законы.
В окружающей нас природе существует множество объектов, являющихся физическими моделями указанной фигуры. Например, многие детали машин имеют форму цилиндра или представляют собой некоторое их сочетание, а величественные колонны храмов и соборов, выполненные в форме цилиндров, подчеркивают их гармонию и красоту.
Греч. − кюлиндрос. Античный термин. В обиходе − свиток папируса, валик, каток (глагол − крутить, катать).
У Евклида цилиндр получается вращением прямоугольника. У Кавальери − движением образующей (при произвольной направляющей − «цилиндрика»).
Цель данного реферата рассмотреть геометрическое тело – цилиндр.
Для достижения данной цели необходимо рассмотреть следующие задачи:
− дать определения цилиндра;
− рассмотреть элементы цилиндра;
− изучить свойства цилиндра;
− рассмотреть виды сечения цилиндра;
− вывести формулу площади цилиндра;
− вывести формулу объема цилиндра;
− решить задачи с использованием цилиндра.
Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

1.1. Определение цилиндра
Рассмотрим какую-либо линию (кривую, ломаную или смешанную) l, лежащую в некоторой плоскости α, и некоторую прямую S, пересекающую эту плоскость. Через все точки данной линии l проведем прямые, параллельные прямой S; образованная этими прямыми поверхность α называется цилиндрической поверхностью. Линия l называется направляющей этой поверхности, прямые s 1 , s 2 , s 3 . − ее образующими.
Если направляющая является ломаной, то такая цилиндрическая поверхность состоит из ряда плоских полос, заключенных между парами параллельных прямых, и называется призматической поверхностью. Образующие, проходящие через вершины направляющей ломаной, называются ребрами призматической поверхности, плоские полосы между ними − ее гранями.
Если рассечь любую цилиндрическую поверхность произвольной плоскостью, не параллельной ее образующим, то получим линию, которая также может быть принята за направляющую данной поверхности. Среди направляющих выделяется та, которая, получается, от сечения поверхности плоскостью, перпендикулярной образующим поверхности. Такое сечение называется нормальным сечением, а соответствующая направляющая − нормальной направляющей.
Если направляющая − замкнутая (выпуклая) линия (ломаная или кривая), то соответствующая поверхность называется замкнутой (выпуклой) призматической или цилиндрической поверхностью. Из цилиндрических поверхностей простейшая имеет своей нормальной направляющей окружность. Рассечем замкнутую выпуклую призматическую поверхность двумя плоскостями, параллельными между собой, но не параллельными образующим.
В сечениях получим выпуклые многоугольники. Теперь часть призматической поверхности, заключенная между плоскостями α и α’, и две образовавшиеся при этом многоугольные пластинки в этих плоскостях ограничивают тело, называемое призматическим телом − призмой.
Цилиндрическое тело − цилиндр определяется аналогично призме:
Цилиндром называется тело, ограниченное с боков замкнутой (выпуклой) цилиндрической поверхностью, а с торцов двумя плоскими параллельными основаниями. Оба основания цилиндра равны, также равны между собой и все образующие цилиндра, т.е. отрезки образующих цилиндрической поверхности между плоскостями оснований.
Читайте также: Цилиндр тень от него
Цилиндром (точнее, круговым цилиндром) называется геометрическое тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов (рис. 1).
1.2. Элементы и свойства цилиндра
Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, − образующими цилиндра.
Так как параллельный перенос есть движение, то основания цилиндра равны.
Так как при параллельном переносе плоскость переходит в параллельную плоскость (или в себя), то у цилиндра основания лежат в параллельных плоскостях.
Так как при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние, то у цилиндра образующие параллельны и равны.
Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.
Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.
Прямой цилиндр наглядно можно представить себе как геометрическое тело, которое описывает прямоугольник при вращении его около стороны как оси (рис. 2).
В дальнейшем мы будем рассматривать только прямой цилиндр, называя его для краткости просто цилиндром.
Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями его оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим.
Цилиндр называется равносторонним, если его высота равна диаметру основания.
Если основания цилиндра плоские (и, следовательно, содержащие их плоскости параллельны), то цилиндр называют стоящим на плоскости. Если основания стоящего на плоскости цилиндра перпендикулярны образующей, то цилиндр называется прямым.
В частности, если основание стоящего на плоскости цилиндра − круг, то говорят о круговом (круглом) цилиндре; если эллипс − то эллиптическом.
Видео:ПОСМОТРИ ЭТО ВИДЕО ОДИН РАЗ #сотка #математика #егэ #егэ2024 #школаСкачать

1. 3. Сечения цилиндра
Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник. Две его стороны − образующие цилиндра, а две другие − параллельные хорды оснований.
В частности, прямоугольником является осевое сечение. Это − сечение цилиндра плоскостью, проходящей через его ось.
Сечение цилиндра плоскостью, параллельной основанию − круг .
Теорема 1. Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.
Доказательство. Пусть β − плоскость, параллельная плоскости основания цилиндра. Параллельный перенос в направлении оси цилиндра, совмещающий плоскость β с плоскостью основания цилиндра, совмещает сечение боковой поверхности плоскостью β с окружностью основания. Теорема доказана.
Площадь боковой поверхности цилиндра.
За площадь боковой поверхности цилиндра принимается предел, к которому стремится площадь боковой поверхности правильной призмы, вписанной в цилиндр, когда число сторон основания этой призмы неограниченно возрастет.
Теорема 2. Площадь боковой поверхности цилиндра равна произведению длины окружности его основания на высоту (S бок.ц = 2πRH, где R − радиус основания цилиндра, Н − высота цилиндра).
а) 
Рис. 4 − Площадь боковой поверхности цилиндра
Пусть P n и Н соответственно периметр основания и высота правильной n-угольной призмы, вписанной в цилиндр (рис. 4, а). Тогда площадь боковой поверхности этой призмы S бок.ц − P n H . Предположим, что число сторон многоугольника, вписанного в основание, неограниченно растет (рис. 4, б). Тогда периметр P n стремится к длине окружности С = 2πR, где R— радиус основания цилиндра, а высота H не изменяется. Таким образом, площадь боковой поверхности призмы стремится к пределу 2πRH, т. е. площадь боковой поверхности цилиндра равна S бок.ц = 2πRH. Теорема доказана.
Площадь полной поверхности цилиндра.
Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. Площадь каждого основания цилиндра равна πR 2 , следовательно, площадь полной поверхности цилиндра S полн вычисляется по формуле S бок.ц = 2πRH+ 2πR 2 .
Читайте также: Роллы цилиндры для йоги
Рис. 5 − Площадь полной поверхности цилиндра
Если боковую поверхность цилиндра разрезать по образующей АT, и развернуть так, чтобы все образующие оказались в одной плоскости, то в результате мы получим прямоугольник АTT1А1, который называется разверткой боковой поверхности цилиндра. Сторона FF1 прямоугольника есть развертка окружности основания цилиндра, следовательно, АА1=2πR, а его сторона АT равна образующей цилиндра, т. е. АT = Н (рис. 5, б). Таким образом, площадь АT∙АА1=2πRH развертки цилиндра равна площади его боковой поверхности.
Видео:Цилиндр, конус, шар, 6 классСкачать

1.5. Объем цилиндра
Если геометрическое тело простое, то есть допускает разбиение на конечное число треугольных пирамид, то его объем равен сумме объемов этих пирамид. Для произвольного тела объем определяется следующим образом.
Данное тело имеет объем V, если существует содержащие его простые тела и содержащиеся в нем простые тела с объемами, сколько угодно мало отличающимися от V.
Применим это определение к нахождению объема цилиндра с радиусом основания R и высотой Н.
При выводе формулы для площади круга были построены такие два n-угольника (один − содержащий круг, другой − содержащийся в круге), что их площади при неограниченном увеличении n неограниченно приближались к площади круга. Построим такие многоугольники для круга в основании цилиндра. Пусть Р − многоугольник, содержащий круг, а Р’ − многоугольник, содержащийся в круге (рис. 6).
Рис. 7 − Цилиндр с описанной и вписанной в него призмой
Построим две прямые призмы с основаниями Р и Р’ и высотой Н, равной высоте цилиндра. Первая призма содержит цилиндр, а вторая призма содержится в цилиндре. Так как при неограниченном увеличении n площади оснований призм неограниченно приближаются к площади основания цилиндра S, то их объемы неограниченно приближаются к SН. Согласно определению объем цилиндра
Итак, объем цилиндра равен произведению площади основания на высоту.
2 Практическая часть (задачи)
Видео:Усеченный конус. 11 класс.Скачать

Задача 1.
Осевое сечение цилиндра − квадрат, площадь которого Q.
Найдите площадь основания цилиндра.
Дано: цилиндр, квадрат − осевое сечение цилиндра, S квадрата = Q.
Сторона квадрата равна . Она равна диаметру основания. Поэтому площадь основания равна .
Видео:№543. Угол между диагоналями развертки боковой поверхности цилиндра равен φ, диагональ равна d.Скачать

Задача 2.
В цилиндр вписана правильная шестиугольная призма. Найдите угол между диагональю ее боковой грани и осью цилиндра, если радиус основания равен высоте цилиндра.
Дано: цилиндр, правильная шестиугольная призма вписанная в цилиндр, радиус основания = высоте цилиндра.
Найти: угол между диагональю ее боковой грани и осью цилиндра.
Решение: Боковые грани призмы − квадраты, так как сторона правильного шестиугольника, вписанного в окружность, равна радиусу.
Ребра призмы параллельны оси цилиндра, поэтому угол между диагональю грани и осью цилиндра равен углу между диагональю и боковым ребром. А это угол равен 45°, так как грани − квадраты.
Ответ: угол между диагональю ее боковой грани и осью цилиндра = 45°.
Видео:№538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевогоСкачать

Задача 3.
Высота цилиндра 6см, радиус основания 5см.
Найдите площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4см от нее.
Дано: Н = 6см, R = 5см, ОЕ = 4см.
Треугольник ОКМ − равнобедренный (ОК = ОМ = R = 5 см),
треугольник ОЕК − прямоугольный.
Из треугольника ОЕК, по теореме Пифагора:
Видео:11 класс, 17 урок, Площадь поверхности конусаСкачать

Задача 4.
Высота цилиндра 12см, радиус основания 10см.
Цилиндр пересечен плоскостью так, что в сечении получился квадрат.
Найдите расстояние от этого сечения до оси.
🔥 Видео
Конус. 11 класс.Скачать

11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Тема 4. Цилиндр. Осевое сечение цилиндра. Развертка боковой поверхности цилиндра. Площадь боковойСкачать

РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

ОТКУДА? Как найти площадь боковой поверхности конуса? Развёртка конуса | Математика с ДетекторомСкачать

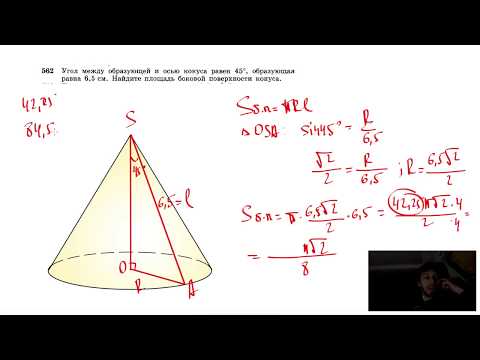
№562. Угол между образующей и осью конуса равен 45°, образующая равна 6,5 см. НайдитеСкачать
Цилиндр. Площадь боковой и полной поверхности цилиндра.Скачать

9 класс, 41 урок, ЦилиндрСкачать

Цилиндр и конус имеют общее основание и высоту. Высота цилиндра равна радиусу основания... (ЕГЭ)Скачать

усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать

Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать