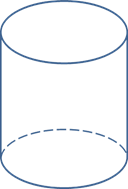
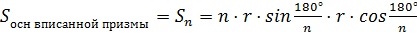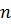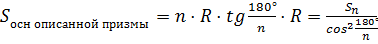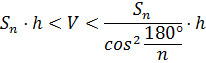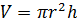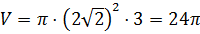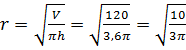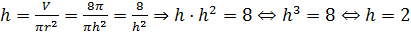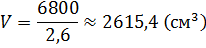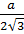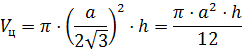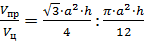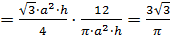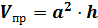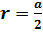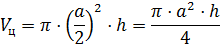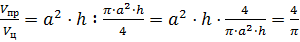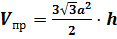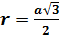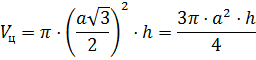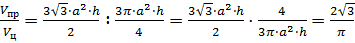Цилиндр (от лат. пер. «цилиндрус«) — каток, валик.
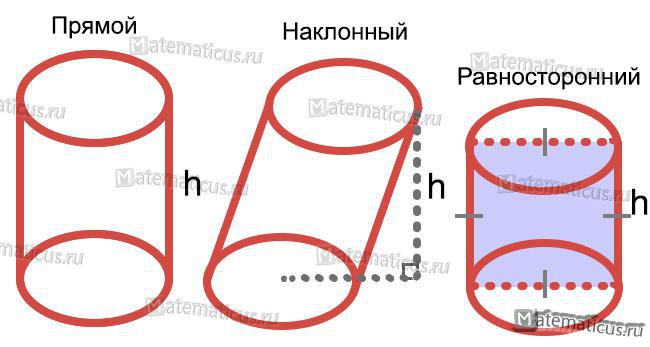
Прямым круговым цилиндром называют часть пространства, заключенной внутри цилиндрической поверхности, лежащей между двумя плоскостями, перпендикулярными образующей.
Равносторонний цилиндр — это цилиндр, у которого диаметр основания равен образующей (то есть осевое сечение — квадрат).
Наклонный цилиндр — это цилиндр, образующие которого не перпендикулярны плоскостям его оснований.
Цилиндр можно получить путём вращения прямоугольника вокруг прямой, содержащей любую его сторону.
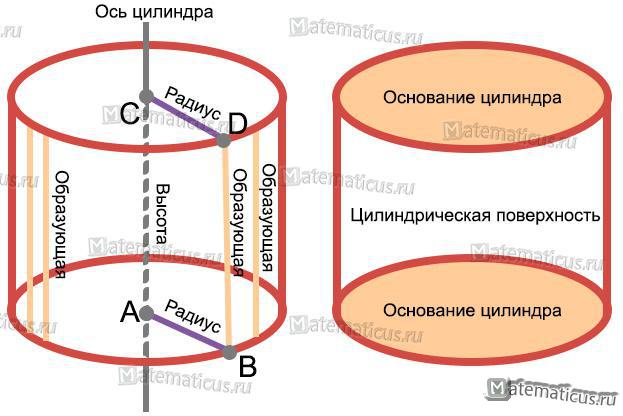
Высотой цилиндра называется расстояние AC между плоскостями его оснований.
Радиус цилиндра — это радиус основания цилиндра CD и AB.
Образующая цилиндра называется отрезок DB, соединяющий соответственные точки двух окружностей.
Сверху и снизу цилиндр ограничен кругами и называются они основаниями цилиндра.
Осью цилиндра – это прямая, проходящая через центры оснований.
Высота цилиндра и его образующая равны между собой.
1) Основания равны и параллельны.
2) Все образующие цилиндра взаимно параллельны и равны.
3) Все высоты цилиндра взаимно параллельны и равны.
Видео:№530. Высота цилиндра равна 12 см, а радиус основания равен 10 см. Цилиндр пересеченСкачать
Объем цилиндра
Урок 24. Геометрия 11 класс ФГОС
Видео:Все типы 3 задания ЕГЭ математика профиль 2024Скачать
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Объем цилиндра»
На этом уроке мы вспомним определение цилиндра, основные элементы цилиндра, выведем формулу для вычисления объёма цилиндра.
Тело, ограниченное цилиндрической поверхностью и двумя равными кругами с границами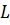 
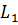
и 
, называется цилиндром.
Читайте также: Заливает свечу второго цилиндра
Можно ещё услышать и такое определение:
Прямым круговым цилиндром или просто цилиндром называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями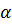 
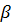
и 
, которые перпендикулярны образующим цилиндрической поверхности.
Назовём элементы цилиндра.
Круги называются основаниями цилиндра.
Отрезки образующих, заключенные между основаниями, — образующими цилиндра.
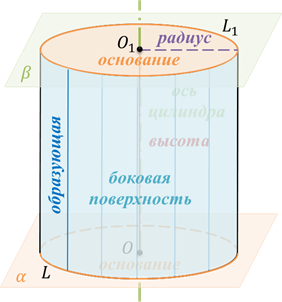
А образованная ими часть цилиндрической поверхности это есть боковая поверхность цилиндра.
Ось цилиндрической поверхности называется осью цилиндра.
Как уже отмечалось ранее, все образующие цилиндра параллельны и равны друг другу. Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.
Цилиндр называется равносторонним, если его высота равна диаметру основания.
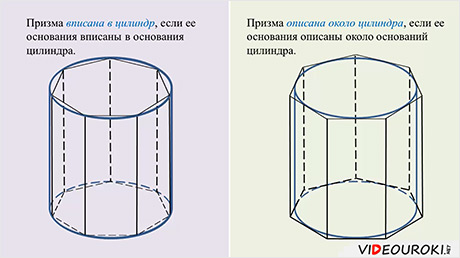
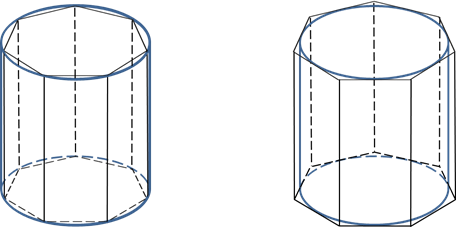
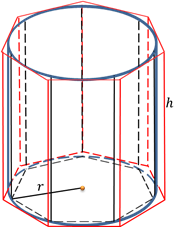
Говорят, что призма вписана в цилиндр, если её основания вписаны в основания цилиндра, и призма описана около цилиндра, если её основания описаны около оснований цилиндра.
Нетрудно увидеть, что высота любой призмы, вписанной в цилиндр или описанной около него, равна высоте самого цилиндра.
Теперь давайте сформулируем и докажем теорему о вычислении объёма цилиндра.
Объём цилиндра равен произведению площади основания на высоту.
Доказательство. Пусть нам дан цилиндр, радиус которого равен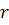 
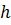
, а высота – 
.
Впишем в этот цилиндр правильную -угольную призму. Поскольку призма правильная, значит, в основании этой призмы лежит правильный -угольник.
Давайте вернёмся в планиметрию и вспомним формулу для нахождения площади правильного многоугольника вписанного около окружности. Поскольку этот многоугольник является основанием прямой призмы, значит, площадь основания призмы будет вычисляться по формуле .
Теперь давайте вокруг этого же цилиндра опишем -угольную призму с таким же количеством сторон.
Вернёмся в планиметрию и вспомним формулу для нахождения площади правильного многоугольника описанного около окружности. Поскольку этот многоугольник является основанием прямой призмы, значит, площадь основания призмы будет вычисляться по формуле .
Читайте также: Задний тормозной цилиндр рено логан 2010 года
Так как эта призма содержится в цилиндре, а цилиндр содержится в этой призме, то, значит, объём цилиндра больше объёма одной призмы и меньше объёма второй призмы.
Объём прямой призмы вычисляется по формуле произведение площади основания призмы на высоту призмы.
Если увеличивать количество сторон основания призмы, то площадь основания призм будет стремиться к площади круга, тогда объём этих призм будет стремиться к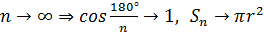 
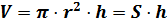
. То есть мы получили, что объём цилиндра вычисляется по формуле 
.
Что и требовалось доказать.
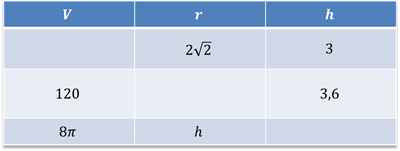
Задача: заполнить таблицу недостающими данными.
Решение: в первой строке нам известны радиус основания цилиндра и высота цилиндра, для того, чтобы найти объём цилиндра, воспользуемся только что доказанной формулой .
Занесём получившееся значение в ячейку.
Во второй строке нам даны объем цилиндра и его высота, для того чтобы найти радиус основания цилиндра, выразим из формулы объёма радиус . Занесём получившееся значение в ячейку.
В третьей строке нам даны: объём цилиндра и его радиус, который равен высоте цилиндра. Подставим эти значения в известную нам формулу и получим .
Задача: алюминиевый провод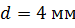 
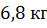
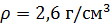
имеет массу 
. Найти длину провода, 
.
Решение: для решения этой задачи, нам нужны будут знания из физики. Мы знаем, что для вычисления массы используется формула: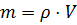 
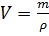
. Тогда нетрудно найти объём 
провода.
Не забудем перевести килограммы в граммы.
Провод представляет собой цилиндр.
Длина провода будет высотой этого цилиндра. То есть наша задача сводится к нахождению высоты цилиндра.
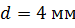
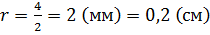
Диаметр провода равен , значит, радиус основания цилиндра будет равен 
.
Из формулы для вычисления объёма цилиндра выразим высоту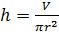 
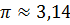
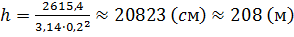
, в качестве 
. Получим, что длина провода приближённо равна 
.
Задача: в цилиндр вписана правильная -угольная призма. Найти отношение объёмов призмы и цилиндра, если призма треугольная, четырёхугольная, шестиугольная.
Читайте также: Крайслер пт крузер рабочий цилиндр сцепления
Решение: применим известные нам формулы для вычисления объёмов правильной призмы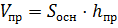 
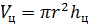
и цилиндра 
.
Сегодня на уроке мы говорили, что если призма вписана в цилиндр, то её высота равна высоте цилиндра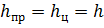 
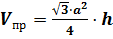
. На предыдущих уроках мы выводили формулы для вычисления объёмов правильных призм. Воспользуемся ими. Применим формулу, связывающую радиус вписанной окружности в правильный многоугольник со стороной многоугольника. Тогда получим, что: если в цилиндр вписана правильная треугольная призма, тогда объём призмы равен 
.
Радиус цилиндра будет равен .
Тогда отношение объёмов правильной призмы и цилиндра будет равно
.
Если в цилиндр вписана четырёхугольная призма, то объём призмы равен
.
Радиус цилиндра будет равен .
Тогда отношение объёмов призмы и цилиндра равно .
Если в цилиндр вписана шестиугольная призма, то объём призмы равен .
Радиус цилиндра будет равен .
Тогда отношение объёмов призмы и цилиндра равно .
Сегодня на уроке мы вспомнили какая фигура называется цилиндром, повторили основные элементы цилиндра, вывели формулу для вычисления объёма цилиндра, рассмотрели несколько задач на применение этой формулы.
🎬 Видео
Видеоурок по математике "Цилиндр"Скачать
Радиус основания цилиндра равен 26, а его образующая равна 9... Найдите площадь сечения.Скачать
Цилиндр и конус имеют общее основание и высоту. Высота цилиндра равна радиусу основания... (ЕГЭ)Скачать
№531. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельнойСкачать
№488. Найдите: а) высоту равностороннего треугольника, если его сторона равна 6 см;Скачать
2065 радиус окружности вписанной в правильный треугольник равен 29 Найдите высоту этого треугольникаСкачать
Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать
11 класс, 15 урок, Площадь поверхности цилиндраСкачать
№523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высотуСкачать
Длина окружности. Математика 6 класс.Скачать
ЦИЛИНДР геометрия егэ по математике профильный уровень ЯщенкоСкачать
Задание 16 ОГЭ по математике. Окружность вписана в равносторонний треугольник.Скачать
№550. Осевое сечение конуса — прямоугольный треугольник. Найдите площадь этого сечения, еслиСкачать
7 класс, 36 урок, Признаки равенства прямоугольных треугольниковСкачать
Все № 3 из Ященко 2024 (36 задач, стереометрия)Скачать
ЗАДАНИЕ 8 из ЕГЭ_50Скачать
Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать
Геометрия 9 класс (Урок№34 - Тела и поверхности вращения.)Скачать
